InteractingFermions: Difference between revisions

From PhyWiki
Jump to navigation Jump to search
 
(One intermediate revision by the same user not shown)
Line 109: Line 109:
In the following, we will work out the relevant and marginal operators describing a system of interacting fermions and provide the foundation for the study of such systems in one or more dimension, which are carried out in section 4 and 5, respectively.
In the following, we will work out the relevant and marginal operators describing a system of interacting fermions and provide the foundation for the study of such systems in one or more dimension, which are carried out in section 4 and 5, respectively.


The fundamental constants characterizing the electronic properties of a solid are the coupling e, the electron mass m and Planck's constant <math>\hbar</math>. From these, we can construct the energy scale <math>E_0=\mathcal{O}(10)\text{eV}</math>, which corresponds  e.g. to the width of the electron conduction band, and hence makes sense as characteristic energy scale. There are two more constants, the mass M of the ions and the speed of light c. Since <math>M\gg m</math> and <math>c\gg v_F</math>, we can treat <math>m/M</math> and <math>v_F/c</math> effects (lattice vibrations and spin-orbit-couplings, respectively) as small pertubations. Near <math>E_0</math>, electrons are subject to strong Coulomb-interactions. We are seeking an EFT that is valid at <math>E\ll E_0</math>. One has to find the correct degrees of freedom to describe this EFT. A guess that turns out to work are spin-1/2 fermions. (One might be tempted to say "This is obvious because the underlying fields are spin-1/2 electrons anyway". However remember that the fields of the EFT theory need not be the same as the fields of the full theory.)
The fundamental constants characterizing the electronic properties of a solid are the coupling e, the electron mass m and Planck's constant <math>\hbar</math>. From these, we can construct the energy scale <math>E_0=\mathcal{O}(10)\text{eV}</math>, which corresponds  e.g. to the width of the electron conduction band, and hence makes sense as characteristic energy scale. There are two more constants, the mass M of the ions and the speed of light c. Since <math>M\gg m</math> and <math>c\gg v_F</math>, we can treat <math>\tfrac{m}{M}</math> and <math>\tfrac{v_F}{c}</math> effects (lattice vibrations and spin-orbit-couplings, respectively) as small pertubations. Near <math>E_0</math>, electrons are subject to strong Coulomb-interactions. We are seeking an EFT that is valid at <math>E\ll E_0</math>. One has to find the correct degrees of freedom to describe this EFT. A guess that turns out to work are spin-1/2 fermions. (One might be tempted to say "This is obvious because the underlying fields are spin-1/2 electrons anyway". However remember that the fields of the EFT theory need not be the same as the fields of the full theory.)


The symmetries of the system are:
The symmetries of the system are:
Line 357: Line 357:
\end{align}
\end{align}
</math>
</math>
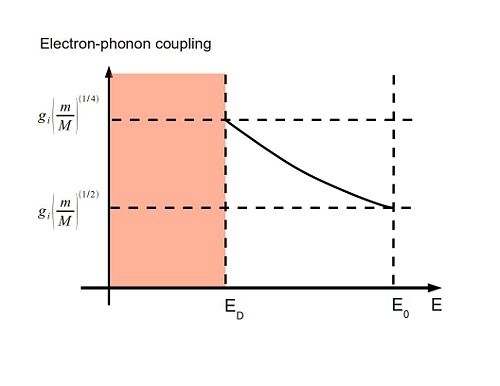
Even if the coefficient of the second term, <math>\Delta_{ij}/M</math> at <math>E_0</math> started out very small, it will increase with <math>s^{-2}</math> when we lower the energy-scale by s. At
Even if the coefficient of the second term, <math>\tfrac{\Delta_{ij}}{M}</math> started out very small  at <math>E_0</math>, it will increase with <math>s^{-2}</math> when we lower the energy-scale by s. At
:<math>
:<math>
   E_D=\left(\frac{m}{M} \right)^{1/2}E_0
   E_D=\left(\frac{m}{M} \right)^{1/2}E_0
Line 377: Line 377:
<math>g_i</math>  in most generality is  a function of the momenta <math>g_i=g_i(\textbf{q},\textbf{k}_1,\textbf{k}_2)</math>, but for simplicity take it to be just a simple constant.
<math>g_i</math>  in most generality is  a function of the momenta <math>g_i=g_i(\textbf{q},\textbf{k}_1,\textbf{k}_2)</math>, but for simplicity take it to be just a simple constant.
This scales as <math>s^{-1+2-3/2}=s^{-1/2}</math> (the <math>\delta</math>-function does not scale because <math>\textbf{q}</math> doesn't) and is relevant!
This scales as <math>s^{-1+2-3/2}=s^{-1/2}</math> (the <math>\delta</math>-function does not scale because <math>\textbf{q}</math> doesn't) and is relevant!
When the phonons decouple at <math>E_D</math>, the dimensionless coefficient of fermion-phonon-interaction above, <math>g_i\left(\frac{m}{M}\right)^{1/2}</math> has grown to
When the phonons decouple at <math>E_D</math>, the dimensionless coefficient of fermion-phonon-interaction above, <math>g_i\left(t\frac{m}{M}\right)^{1/2}</math> has grown to
:<math>
:<math>
   g_i(E_D)\left(\frac{m}{M}\right)^{1/2}=g_i\left(\frac{E_D}{E_0}\right)^{-1/2}\left(\frac{m}{M}\right)^{1/2}=g_i\left(\frac{m}{M}\right)^{1/4}
   g_i(E_D)\left(\frac{m}{M}\right)^{1/2}=g_i\left(\frac{E_D}{E_0}\right)^{-1/2}\left(\frac{m}{M}\right)^{1/2}=g_i\left(\frac{m}{M}\right)^{1/4}

Latest revision as of 12:02, 9 December 2010

Introduction

One of the most beautiful aspects of physics is the versatility of ideas and methods. An approach that is developed for a specific problem in a specific field may turn out to be very powerful for a completely different application. One example of such a basic, but extremely powerful tool is the idea of symmetries and in particular broken symmetries. (Broken symmetries are, in spite of their quite misleading name, perfectly valid symmetries only realized in less straightforward way than unbroken symmetries.) In this work, the method of effective field theories (EFTs) and the Renormalization group (RG), applied to interacting fermions, will be discussed. EFTs are typically associated with particle physics, the classical example being the Fermi theory of the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta} -decay. However, their usefulness is by far not confined to this field as will be showed in the following. This work is based mainly on the review article by R. Shankar [1] and a TASI lecture by Polchinski [2].

Effective Field theory and the Renormalization group

Basic idea

Consider a quantum field theory that has a characteristic energy scale Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_0} . Suppose on is interested only in the physics at Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle E\ll E_0} . In that case, effects at low energy can be described very well by an Effective Field Theory (EFT). The EFT can look very different from the "full" high energy theory, it can have different interactions and even be written in terms of different fields. One example of an EFT that differs a lot from the underlying full theory is Chiral Pertubation Theory (ChPT), enabling physicists to make prediction in the low energy, strongly coupled regime of QCD. While the fundamental fields are quarks and gluons, the low energy theory is described in terms on pions, Kaons etc. This example also illustrates why EFTs are useful: Not only can they facilitate computations, in cases when the full theory is strongly coupled and perturbation theory breaks down they are the only way to go.

Suppose your theory contains a scalar fields Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi} . Choose a cutoff Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Lambda} at roughly Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_0} and write

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi=\phi_H + \phi_L }

where

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \phi_H:& \omega >\Lambda\qquad \text{high-frequency part of }\phi \\ \phi_L:&\omega<\Lambda\qquad \text{low-frequency part of }\phi \end{align} }

The action is rewritten as

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} S(\phi_L,\phi_H)=S_0(\phi_L)+S_0(\phi_H)+S_I(\phi_L,\phi_H) \end{align} }

Where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_0} is quadratic in the fields and contains either only Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi_L} or only Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi_H} . The interactions encoded by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_I} can mix Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi_L} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi_H} . And the generating functional is

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \int_{\omega<\Lambda} \mathcal{D} \phi_L\int_{\omega>\Lambda} \mathcal{D} \phi_H e^{i S(\phi_L,\phi_H)}=\int_{\omega<\Lambda} \mathcal{D} \phi_Le^{i S_0(\phi_L)}\underbrace{\int_{\omega>\Lambda} \mathcal{D} \phi_He^{i S_I(\phi_L,\phi_H)} e^{i S_0(\phi_H)}}_{\equiv\exp[iS_\text{eff}(\phi_L)]} \end{align} }

where we defined the effective action Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_\text{eff}(\phi_L)} .

If the full action Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S(\phi_L,\phi_H)} is known, we can calculate the effective action from the definition above. But even if we have no clue about the full theory, we can still expand in terms of all operators Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{O}_i} that are compatible with the symmetries of the problem:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} S_{\text{eff}}=\int d^D x \sum_i g_i \mathcal{O}_i \end{align}}

This is an infinite sum, but we will see that we can classify the operators by dimensional analysis and that only a handful of operators will turn out to be actually important.

Relevant, marginal and irrelevant operators

In units of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hbar=1} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c=1} , the action is dimensionless, so if an operator Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{O}_i} in the effective action is of mass-dimension Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle d_i} it follows that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle g_i} has to be of dimension Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D-d_i} where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D} is the dimension of the physical system. Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle d_i} can be read of from the operator in question if we know the dimensions of the fields in question. If the theory is weakly coupled, it is obtained from the kinetic term of the free action. For a scalar field, this would be

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \frac{1}{2} \int d^Dx \partial_\mu \phi \partial^\mu \phi \end{align} }

which tells us that the dimension of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi} has to be Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (-1+D/2)} in order for the entire term to be dimensionless. Instead of the dimensionfull couplings Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle g_i} , one often uses the dimensionless couplings Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda_i=E_0^{D-d_i}g_i} where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_0} is the characteristic energy scale of the system in question and the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda_i} are roughly of order one. Now, calculating a process at some different energy scale Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Lambda} , by dimensional analysis we expect the magnitude of a term in the effective action to be

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int d^D x \mathcal{O}_i \sim \Lambda^{d_i-D} }

implying that the term is of the order of

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda_i \left( \frac{\Lambda}{E_0}\right)^{d_i-D} }

If we go low energies, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle \Lambda \ll E_0} , we find three types of behavior depending on the sign of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle d_i-D} . Terms with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle d_i>D} will become heavily suppressed, those are called irrelevant. Terms with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle d_i<D} will be enhanced, those we call relevant. Finally, if Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle d_i=D} , the term is not directly affected by the ratio of scales, and the corresponding operator is called marginal.

While the dimensional analysis is popular in high energy physics, there is another equivalent way to think about this. Typically we consider processes that take place below a certain energy, and decrease the limiting energy (cutoff) further and further. To do this, scale all energies and momenta by a factor Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle s<0} . From the kinetic term, such as the one of the scalar field given at the beginning of this section, we find that the field fluctuations scale as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle s^{-1+D/2}} , so we can determine the scaling Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle s^{d_i}} for each operator and find that the individual terms in the effective action scale as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle s^{d_i-D}} . Our early observations about which terms decrease, increase or stay remain the same.

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle d_i} behavior under Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E\to 0} classification
< D increases relevant
=D unchanged marginal
>D decreases irrelevant

At very low energies, irrelevant operators are so much suppressed that, up to corrections of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{O}\left( \tfrac{\Lambda}{E_0}\right)} , it is valid to forget about them entirely. Typically, there is only a handful of relevant and marginal operators whose effects need to be investigated.

The Renormalization Group

The idea of renormalization is to make use of the invariance of any physical theory under changes of the cutoff-scale Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Lambda} . In spite its name, the renormalization group is not a group in the mathematical sense. Why does such a cutoff scale appear? By definition, an effective theory is obtained as the low energy limit of a high energy full theory. Then Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Lambda} is just the value representing the watershed between "low" and "high" energies. The appropriate Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Lambda} of the effective theory for the weak interactions would be of the order of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m_W=80} GeV. Above this energy, W and Z bosons cannot be integrated out anymore, the effective theory breaks down and must be replaced by the full high energy theory, containing dynamical W and Z bosons. But the appearance of a cutoff is not constrained to effective theories. In QED, which is the full theory for interactions between leptons and photons for all we know, physical quantities such as scattering cross-sections can be expanded in orders of the coupling Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha} . All coefficients except that of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha^0} (the tree level contribution) contain integrals over particle momenta k, which extend up to infinity and diverge. This is apparently at odds with experiments, which gives us finite results for all physical quantities. The integrals must be "tamed", and the corresponding procedure is called "Regularization". The most straightforward (but not always practical approach) is to choose a finite upper bound Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Lambda} and integrate over Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k<\Lambda} (hence "cutoff"). Other regularization schemes contain the high energy scale Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Lambda} in other ways. Since Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Lambda} is an artificial entity in the first place, it is immediately evident that no physical observable can depend on it, hence there must exist a scaling symmetry under changing Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Lambda \to s \Lambda} , where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle s} is some arbitrary number.

(In an EFT, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Lambda} is physical in the sense that it corresponds to the energy limit where the EFT will stop to work. The argumentation still works, since the low energy physics should not be affected by shifts in Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Lambda} as long as one is interested only in effects at energies Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ll \Lambda} .)

Running couplings

How is this symmetry realized? Qualitatively speaking, the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Lambda} -dependance introduced by regularization has to be neutralized. For a scattering cross-section, as the coefficients of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha^2} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha^3} , ... become functions of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Lambda} , we can redefine Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha} as function of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Lambda} in such a way that the cross-section is independent. In fact, it is possible to redefine the parameters in the theory (Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha} and m in QED) and make them Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Lambda} -dependent in such that each and every observable is finite. (This is a non-trivial statement because there is only a handful of parameters to adjust, but in principle an infinite amount of observables)

In an effective theory, the couplings of relevant and irrelevant operators are directly dependent on Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Lambda} of course. The behavior of marginal is more intricate, since any small correction from naive scaling will push those to be either relevant or irrelevant. To classify the behavior of marginal couplings, one defines the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta} -function:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta(g)=\frac{\text{d} g}{\text{d} \ln \Lambda} }

(I use the field theory convention here. In [1], the definition carries an extra minus sign.)

If for one particular value Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle g^\ast} the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta} -function Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta(g^\ast)=0} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle g^\ast} is called a fixed point.

Usually, the coupling will behave like

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta(g)=c g^2+\mathcal{O}(g^3) }

Integrating gives the following expression

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle g(E)=\frac{g(E_0)}{1+c g(E_0)\ln (E_0/E)} }

The couplings strength depends on the energy scale. This is referred to as "running couplings".

The RG approach to interacting fermions

Can the ideas of EFTs be applied to condensed matter systems, like for example a metal consisting of a lattice of ions in a "jellyum" of electrons?

In the following, we will work out the relevant and marginal operators describing a system of interacting fermions and provide the foundation for the study of such systems in one or more dimension, which are carried out in section 4 and 5, respectively.

The fundamental constants characterizing the electronic properties of a solid are the coupling e, the electron mass m and Planck's constant Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hbar} . From these, we can construct the energy scale Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_0=\mathcal{O}(10)\text{eV}} , which corresponds e.g. to the width of the electron conduction band, and hence makes sense as characteristic energy scale. There are two more constants, the mass M of the ions and the speed of light c. Since Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle M\gg m} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c\gg v_F} , we can treat Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tfrac{m}{M}} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tfrac{v_F}{c}} effects (lattice vibrations and spin-orbit-couplings, respectively) as small pertubations. Near Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_0} , electrons are subject to strong Coulomb-interactions. We are seeking an EFT that is valid at Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E\ll E_0} . One has to find the correct degrees of freedom to describe this EFT. A guess that turns out to work are spin-1/2 fermions. (One might be tempted to say "This is obvious because the underlying fields are spin-1/2 electrons anyway". However remember that the fields of the EFT theory need not be the same as the fields of the full theory.)

The symmetries of the system are:

  1. electron number conservation
  2. discrete lattice translational symmetry, therefore only discrete amounts of momentum can be exchanged with the lattice. In the following for simplicity we will mostly treat momentum as exactly conserved.
  3. discrete point symmetries of the crystal
  4. Spin symmetry. In the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c\to \infty} limit, this is an internal Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle SU(2)} symmetry.

In an EFT, it is not valid to guess a specific Hamiltonian. Instead we have to consider all possible operators, and classify them into relevant, marginal and irrelevant operators. Irrelevant operators will have no effects on the low energy EFT, so we will only have to investigate effects from relevant and marginal operators. We will see that there is only one relevant operator, which modifies the Fermi-surface and one possibly marginal operator that encodes interactions. The free, non-relativistic action is:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int d t d^Dp \left\{i \psi^\dagger_\sigma(p) \partial_t \psi_\sigma(p)-(\varepsilon(p)-\varepsilon_F)\psi^\dagger_\sigma(p) \psi_\sigma(p) \right\} }

where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma} labels the spin and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \varepsilon_F} is the Fermi energy.


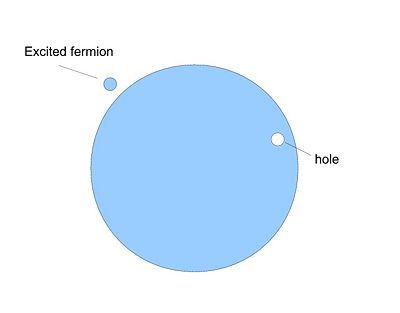
Fig. 1 Schematic picture of quasi-particles and quasi-holes, the low energy excitations of the Fermi Sea.

In the ground state, all the states with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \varepsilon(p)<\varepsilon_F} are occupied, all states with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \varepsilon(p)>\varepsilon_F} are empty (Fermi Sea). We excite this ground state by removing one fermion from the sea (creating a hole) and placing it above the Fermi surface. Low energy exitations are those where the excited particle and the hole are both very close to the Fermi surface. This corresponds to the picture of "quasi-particles"/"quasi-holes" in Landau Fermi-liquid theory.

Next we need to find the behavior of the fields when all energies are scaled by a factor Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle s<1} . Note that this means that the momenta scale towards the Fermi surface and not to zero, as one might is used to from other EFTs. Further note that any momentum p can be decomposed into a component l orthogonal to the Fermi surface and a tangent component k. In particular Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle d^D p=d^{D-1}k d l} . Furthermore, for our low energy excitations, we can expand

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E(p)= (\varepsilon(k,l<)-\varepsilon_F)=l v_F(k)+\mathcal{O}(l^2) }

where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle v_F=\partial_p \varepsilon|_{\varepsilon=\varepsilon_F}} is the Fermi velocity. Under scaling, the tangential component remains unchanged while Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle l\to s l} . Thus, when Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E\to s E} we find the following scaling properties

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} dt&\to s^{-1} dt & d^{D-1} k &\to d^{D-1} & l&\to sl &d l &\to s d l & \partial_t &\to s \partial_t \end{align} }

We then find that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi} needs to scale with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle s^{-1/2}} to make the free, non-relativistic action given above invariant.

In an EFT, all operators that are allowed by symmetry are expected. Do we find any such operators that are not irrelevant?

  • terms quadratic in Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi} :
    Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int dt\; d^{D-1}k\; dl\; \mu(k)\psi^\dagger_\sigma(p) \psi_\sigma(p)}
    Can be absorbed into the definition of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \varepsilon(p)} . This tells us that while a Fermi surface determined by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \varepsilon(p)=\varepsilon_F} has to exist, it would be unnatural to assume any specific shape of this Fermi surface (except for symmetry constraints).
  • quartic interactions:
    Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int dt \; d^{D-1}k_1 dl_1\; d^{D-1}k_2 dl_2 \; d^{D-1}k_3 dl_3 \; d^{D-1}k_4 dl_4 \;V(p_1,p_2,p_3,p_4)\;\psi^\dagger_\sigma(p_1) \psi_\sigma(p_2)\psi^\dagger_{\sigma'}(p_3) \psi_{\sigma'}(p_4)\delta^D(p_1+p_2-p_3-p_4) }

    The interaction scales like Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle s^{-1+4-2}=s^1} times the scaling of the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta} -function. The scaling of the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta} -function depends on the specific momentum configuration and can be either Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta(\ldots)\to s^{-1}\delta(\ldots)} (if Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle l_i} dominate) or Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta(\ldots)\to s^0\delta(\ldots)} (if Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k_i} dominate). Therefore, the coupling V can be either marginal or irrelevant.
  • any further interactions (Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi^6} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi^8} ) are always irrelevant.

Interacting fermions in d=1

Let's consider fermions in 1 dimension, and for simplicity assume that they are spinless. While this is clearly a theoretical construction, spin is merely "an unessential complication if we are simply trying to understand how the RG works" [1]. In the spinless case, there can be only one (instead of two) fermion at each site. Half-filling therefore means one particle on every other site.

To show the advantages of the RG-approach, in subsection 4.1, we will first consider the system in mean-field theory, only to find that this gives a result in disagreement with experiment. In subsection 4.1, the correct result is obtained in RG/EFT language.

Failure of mean-field theory

In the following, the lattice spacing is set to 1, such that the real space and reciprocal lattice vectors are Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle R_j\equiv j} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle K_j\equiv\tfrac{2 \pi}{j}} .

Now let's consider a specific Hamiltonian

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H=\underbrace{-\frac{1}{2} \sum_j \psi^\dagger(j+1) \psi (j)+h.c.}_{H_0} +\underbrace{V_0 \sum_j \left[\psi^\dagger(j)\psi(j)-\frac{1}{2}\right]\left[\psi^\dagger(j+1)\psi(j+1)-\frac{1}{2}\right]}_{H_I} }

The fermion fields anticommute :Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \{\psi^\dagger(j),\psi(l)\}=\delta_{jl}} .

  • the first term is a "hopping term"
  • the second term describes nearest neighbor repulsion of strength Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_0}
  • symmetries: Note that the Hamiltonian is symmetric under simultaneous interchange of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi^\dagger \leftrightarrow \psi} and changing the sign of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi^\dagger, \psi} on just one sub-lattice. (In fact, the interaction Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H_I} is even symmetric under Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi^\dagger \leftrightarrow \psi} alone) This means the Lagrangian is invariant under interchanging particles with holes Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(n=\psi^\dagger\psi \leftrightarrow \psi^\dagger \psi=1-n\right)} which implies the ground state to have Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle n \rangle=\frac{1}{2}} . This corresponds to half-filling.

Now, before going into details, consider the following extreme cases

  • Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_0=0}
    The Hamiltonian in k-space reads
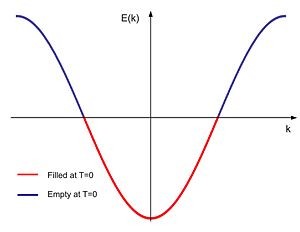
    Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} H=&H_0=\int_{-\pi}^\pi \frac{d k}{2 \pi}\psi^\dagger(k)\psi(k)E(k) &\text{where } E(k)&=-\cos(k) \end{align} }
    At half filling, all states with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |k|\leq k_F=\tfrac{\pi}{2}} will be occupied, all others will be empty. The Fermi surface in one dimension consists only of the two points Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k = \pm \tfrac{\pi}{2}} .
Cosine.jpg
  • Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_0=\infty} : In this case, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H_0} can be neglected against Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H_I} . The interactrion Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H_I} will be minimized if no fermion has a neighbor, this means either all even or all odd sites are filled. This state clearly breaks the translational symmetry of the lattice, and is called a "Charge-Density-Wave" or CDW state.
CDW.jpg

Knowing the two extreme cases, what will happen for small, but non-zero Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_0} values? Let's write Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi^\dagger(j)\psi(j)= n_j} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n_j=\langle n_j \rangle + :n_j:} . Here Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle :n_j:} is normal-ordered and has no expectation value in the ground state. (Note that "having no expectation value" is the definition of normal-ordered here. For a field theorist the operator Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n=\psi^\dagger \psi} might have looked normal-ordered (because it has creation operators to the left and annihilation operators to the right) but it is not because Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n_i} has a non-zero expectation value at half filling.)

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle n_j \rangle} is the fermion number expectation value at site j for which we will make the ansatz

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle n_j \rangle=\frac{1}{2} + \frac{1}{2}(-1)^j \Delta }

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta} is the CDW order parameter. For Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_0\to 0} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta\to 0} , and the probability for each site to be occupied is exactly 1/2. For Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_0\to \infty} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta\to 1} , all even sites will be filled, all odd sites will be empty.

Inserting our ansatz into the Hamiltonian we started out with, we obtain

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} H&=-\frac{1}{2}\sum_j\psi^\dagger(j+1)\psi(j)+h.c. \\ &\qquad+V_0\left[-\frac{1}{4} \sum_j \Delta^2-\sum_j (-1)^j:n_j:\right]+V_0\sum_j :n_j: :n_{j+1}:\\ &=-\frac{1}{2}\sum_j\psi^\dagger(j+1)\psi(j)+h.c.\\ &\qquad+V_0\left[-\frac{1}{4} \sum_j \Delta^2-\sum_j (-1)^j(n_j-\frac{1}{2}-\frac{1}{2}(-1)^j\Delta)\right]+V_0\sum_j :n_j: :n_{j+1}:\\ &=-\frac{1}{2}\sum_j\psi^\dagger(j+1)\psi(j)+h.c.\\ &\qquad+V_0\left[\frac{1}{4} \sum_j \Delta^2-\sum_j (-1)^jn_j\right]+V_0\sum_j :n_j: :n_{j+1}:\\ &=\frac{1}{4}V_0\sum_j \Delta^2+\int_0^\pi \frac{d k}{2 \pi} \left( \psi^\dagger (k), \psi^\dagger (k') \right)\left( \begin{array}{cc} E(k) & -V_0 \Delta\\ -V_0 \Delta & E(k') \end{array} \right) \left( \begin{array}{c} \psi (k) \\ \psi (k') \end{array} \right) \end{align} }

The reason for the mixing of states with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k'=k+\pi} is the factor Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (-1)^j} which multiplies Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n_j=\psi^\dagger(j)\psi(j)} . In Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k} -space, therefore, we will find a term of the form

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_j\iint d k d k' e^{i (k-k'+\pi)j}\psi^\dagger(k)\psi(k')} .

Evaluating the sum gives Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta(k-k'+\pi)} , so in the integral over Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k'} only the term with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k'=k+\pi} contributes. Note that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E(k')=-\cos(k+\pi)=-E(k)} .

Diagonalizing of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H} gives for the ground state energy:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{ E_0(\Delta)}{2 \pi \delta(0)}=\int_0^\pi \frac{d k)}{2\pi}\sqrt{E^2(k)+\Delta^2 V_0^2}+\frac{\Delta^2 V_0}{4} }

Minimizing this w.r.t. Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta} we obtain the following gap equation (assuming Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta \neq 0} )

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1=V_0 \int_0^\pi \frac{1}{\sqrt{E^2(k)+\Delta^2 V_0^2}} }

The integrand is maximal around the Fermi points, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |k|=k_F=\pm \tfrac{\pi}{2}} , where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E(k)} vanishes. Expanding around Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k_F} gives Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E(k_F+q)=q+\ldots} where we restrict Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |q|\leq \Lambda} so that we end up with

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1=V_0 \int_0^\pi \frac{1}{\sqrt{E^2(k)+\Delta^2 V_0^2}}\simeq \frac{2 V_0}{\pi}\ln \frac{\Lambda}{\Delta V_0} \Rightarrow \Delta=\frac{\Lambda}{V_0}e^{-\pi/2 V_0} }

Thus we have shown that for arbitrary small Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_0} , there is a non-zero solution for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta} in mean-field-theory. This implies CDW states no matter how small the interaction. That is in disagreement with experiment, so we need something better than mean-field theory to describe our one dimensional system.

RG in d=1: Luttinger Liquid

The Fermi surface in one dimension consists only of 2 points, labelled L and R, respectively. Therefore, using the definitions of section 3, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p=R+l} or Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p=L+l} , where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |l|\leq \Lambda} . Under scaling, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Lambda \to s^{-1} \Lambda} , and we will be considering a low energy EFT, where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Lambda << k_F} . The transfered momentum in a scattering interaction will be smaller than Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Lambda} , thus it is impossible to transform a state at L into a state at R, and vice versa. The number of L and R in any scattering process is conserved, and the Fermi points drop out of the momentum conserving Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta} -function. Therefore, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta(p_1+p_2-p_3-p_3)=\delta(l_1+l_2-l_3-l_4) \to \delta(sl_1+sl_2-sl_3-sl_4)=s^{-1}\delta(l_1+l_2-l_3-l_4)} , and the coupling V is marginal. To determine the ultimate fate of this coupling, we have to calculate the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta} -function at 1-loop level.

To simplify:

  • To keep it simple and to be able to compare with the mean-field-approach, we consider spinless fermions. (Just to drop the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma} index in everything we did in section 3.)
  • The coupling V is a general function of the (discrete) labels R,L and the (continuous) variables Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle l_i} . Consider only the dependence on Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle l_i} first:
    Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V=V_0+V_i l_i+ V_{ij}l_i l_j+\ldots}
    Under scaling, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V(l_i) \to V(s l_i)} , so we find that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_0 \to s^0 V_0} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_i \to s V_{i}} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_{ij} \to s^2 V_{ij}} , ... . Only the constant term Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_0} is marginal, while the higher coefficients are all increasingly irrelevant. Therefore, we can take V to only depend on its discrete labels: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V=V_{A,B,C,D}} where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A,B,C,D =\{L, R\}} . By Fermi-statistics, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi(R)\psi(R)=\psi(L)\psi(L)=0} and similar for the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi^\dagger} fields. Therefore, all couplings with A=B or C=D vanish. Using antisymmetry further, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi(R)\psi(L)=-\psi(L)\psi(R)} etc. we can reduce our parameter space to only one coupling
    Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V=V_{LRLR}=V_{RLRL}=-V_{LRRL}=-V_{RLLR} }


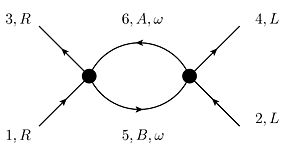
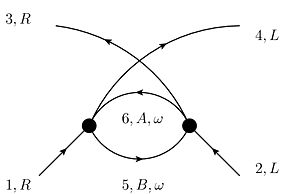
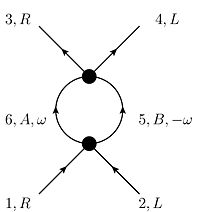
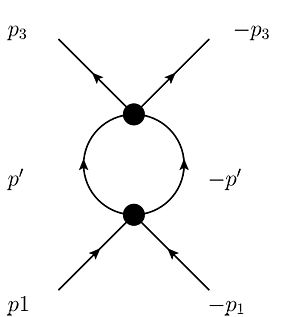
The following diagrams contribute to V at 1-loop-level:

  • The so-called ZS-graph:
1d ZS.jpg

This graph is proportional to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_{3651}V_{4526}=V_{LABL}V_{RBRA}} . The first factor is only non-zero if A=B=R, the second only if A=B=L. Therefore, this diagram is always zero.

  • The so-called ZS'-graph:
1d ZSprime.jpg

This graph is proportional to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_{4651}V_{3526}=V_{LABR}V_{RBLA}} which survives only for A=R,B=L, so the graph is proportional to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_{LRLR}V_{RLLR}=-V_0^2} .

  • The so-called BCS-graph:
1d BCS.jpg

This graph is proportional to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_{3465}V_{5612}=V_{RLAB}V_{BARL}} which is nonzero for A=L,B=R and A=R,B=L. Thus, the graph is proportional to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_{RLLR}V_{RLRL}=V_{RLRL}V_{RLLB}=-V_0^2}

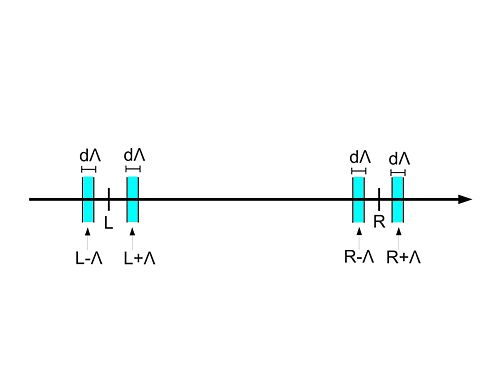
Fig 2: Momentum space slices being integrated out in the d=1 spinless fermion problem.

In the 1-loop calculation, the internal "high energy" modes are integrated out. Since we are only interested in how the contributions to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_0} change as we decrease Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Lambda \to \Lambda - d \Lambda} , we only need to integrate over infinitesimal slices of thickness Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle d \Lambda} located Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \pm \Lambda} away from the Fermi-points L and R (see fig. 2) The ZS'-graph gives the following contribution to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_0} :

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} d V_{0,ZS'}&=-V_0^2 \int_{-\infty}^{\infty}\int_{d \Lambda \in L}\frac{d \omega}{d l}\frac{1}{i \omega -E_L(l)}\frac{1}{i \omega +E_L(l)}\\ &=\frac{V_0^2}{4 \pi v_F}\int_{d \Lambda \in L}\frac{d l}{|E(L+l)|}\\ &=\frac{V_0^2}{2 \pi v_F}\frac{d \Lambda}{\Lambda}x \end{align} }

In the first line, we have Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \pm E_L(l)} in the propagator, because there is a LL and a RR line and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_L(l)=-E_R(l)} . To perform the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle d \omega} integral, we closed the contour integral in the lower half plane, picking up the pole at Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega=-i |E_L(l)|} . (Closing in the upper half plane would pick up the pole at Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega=i |E_L(l)} and give exactly the same result.) In the third line, we have performed the integration over Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int_{d \Lambda \in L}=\int_{-\Lambda}^{-\Lambda + d \Lambda}+\int_{\Lambda-d \Lambda}^{\Lambda}} and used that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_L(l)=v_F l} . We find that V increases when we decrease the cutoff Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Lambda} (remember that we changed Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Lambda} by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -d \Lambda} ), so comparing with the two last equations in subsection 2.4 we find

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \beta_{ZS'}=-\frac{V_0^2}{2 \pi v_F} \end{align} }

Similarly, we get as contribution from the BCS-graph

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} d V_{0,\text{BCS}}&=-V_0^2 \int_{-\infty}^{\infty}\int_{-\Lambda}^{\Lambda}\frac{d \omega}{d l}\frac{1}{i \omega -E_L(l)}\frac{1}{-i \omega -E_L(l)}\\ &=-\frac{V_0^2}{2 \pi v_F}\frac{d \Lambda}{\Lambda}\\ \beta_{\text{BCS}}&=\frac{V_0^2}{2 \pi v_F} \end{align} }

Thus, the total Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta} -function describing the running of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_0} is

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta_{V0}=\beta_{ZS'}+\beta_{\text{BCS}}=0 }

The one dimensional system is a scale invariant Luttinger liquid!

The mean-field theory approach neglected the BCS term, and predicted the CDW instability. In fact, this instability is cancelled by a BCS instability of exactly the same size.

More than one dimension: The Landau Fermi-liquid

Landau's theory of the Fermi liquid, which explains the properties of conductors the interactions of "quasi-particles" close to the fermi-surface, has had remarkable success. For example it explains the existence of collisionless "zero sound" collective modes, and the occurrence of ferromagnetic ("Stoner") instabilities as well as the Mott transition [3]. We will show that Landau's Fermi-liquid theory is obtained automatically when considering a conductor from the point of view of effective theories. The EFT picture explains why weakly coupled spin-1/2 "quasiparticles" describe the conductor so well, even if the underlying electrons are subject to Coulomb-interactions that are by no means "weak". We will set Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle d=3} in the following.

Non-irrelevant Interactions

In section 3, we showed that the only potentially marginal interaction is the 4-fermion interaction:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int dt \; d^{2}k_1 dl_1\; d^{2}k_2 dl_2 \; d^{2}k_3 dl_3 \; d^{2}k_4 dl_4 \;V(p_1,p_2,p_3,p_4)\; \psi^\dagger_\sigma(p_1) \psi_\sigma(p_2)\psi^\dagger_{\sigma'}(p_3) \psi_{\sigma'}(p_4)\delta^3(p_1+p_2-p_3-p_4) }

Since the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle l_i} are restricted to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |l_i|<\Lambda} , whereas the tangential momenta Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k_i} are arbitrary, in general the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k_i} dominate the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta} -function and therefore the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta} -function is invariant under scaling:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta(p_1+p_2-p_3-p_4)\sim \delta(k_1+k_2-k_3-k_4) \qquad \Rightarrow \delta \to s^{0}\delta }

In this case the coupling is irrelevant! As Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E\to 0} , the system becomes more and more free. Therefore, describing the conductor by a gas of nearly free fermions is consistent, even if it seems counterintuitive when one has the electrons of the full theory at Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_0} in mind which are subject to significant Coulomb forces. The EFT legitimizes the underlying assumption of Landau's Fermi-liquid theory.

There are two caveats, which we will discuss in the following. The first is phonons: Our crystalized system exhibits spontaneously broken continous translational symmetry, therefore the low energy theory needs to include the correspinding Goldstone bosons. Phonons will be discussed in the next subsection, 5.2. The second one is that there is one special momentum configuration where the approximation for the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta} -function above does not hold.

Consider a scattering process where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p_{1,2}} scatter into

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} p_3&=p_1+\Delta k_3+\Delta l_3 & p_4=p_2+\Delta k_4+\Delta l_4 \end{align} }

and the momentum conserving Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta} -function is

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta(\Delta k_3+\Delta l_3-\Delta k_4-\Delta l_4) }

If however Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p_1=-p_2} , the tangent vectors to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p_1} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p_2} in the plane spanned by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p_1} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p_2} automatically sum up to zero. Then one component of the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta} -function constrains the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle l} instead of the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k} , and therefore the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta} -function scales as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle s^{-1}} just like in the one dimensional case.

Then, the interaction is marginal in any process where the momenta of two incoming lines add up to zero (by momentum conservation the momenta of the two outgoing fermion lines then also add up to zero).

The flow of this coupling is determined by calculating the BCS-type diagram:

3d BCS.jpg

There is no ZS'-type contribution as in the 1D-case, because momentum conservation in the ZS'-type diagram forces at least one coupling to be irrelevant.

By scaling arguments, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V(p_1,p_2,p_3,p_4)=V(k_1,k_2,k_3,k_4)+\text{irrelevant terms}} . Let's focus on the simplest case where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V(k_1,k_2,k_3,k_4)} is a constant. Then a calculation completely analogous to the one performed for the BCS-diagram in 1D gives:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \beta(V)&=\frac{V^2}N& \text{where}\quad N=\int \frac{d^2 k'}{(2 \pi)^3}v_F(k') \end{align} }

N is the density of states at the Fermi energy. Using the last equation given in section 2.4, we find that if the coupling is known at a certain energy scale Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V\equiv V(E_0)} , at a scale V it has the value

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V(E)=\frac{V}{1+N V \ln (E_0/E)} }

Phonons

Introduce a (bosonic) phonon field Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \textbf{D}(\textbf{r})=\sqrt{M}\textbf{u}(\textbf{r})} where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \textbf{u}(\textbf{r})} are the displacements from the equilibrium position of the ions. The free action of the phonons is

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{2} \int d t d^3 q \left(\partial_t D_i(\mathbf{q})\partial_t D_i(-\mathbf{q})-M^{-1}\Delta_{ij}(\mathbf{q})(D_i(\mathbf{q})D_j(-\mathbf{q})\right) }

where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta_{ij}} describes the restoring force (spring constant) of the oscillating ion. The factor of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle M^{-1}} in front of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta_{ij}} stems from the definition of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{D}(\mathbf{r})} and supresses this term. In typical phonon-electron interactions responsible for BCS superconductivity, an electron absorbs or emits a phonon of large momentum q, but remains near the Fermi surface. Therefore, q does not scale. Because Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle dt \to s^{-1}t} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \partial_t \to s \partial_t} , we find that the phonon field and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta_{ij}} scale as

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \mathbf{D}(\mathbf{q})\to s^{-1/2} \mathbf{D}(\mathbf{q}) &\qquad \text{and} \qquad \Delta_{ij}\to s^{-2}\Delta_{ij} \end{align} }

Even if the coefficient of the second term, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tfrac{\Delta_{ij}}{M}} started out very small at Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_0} , it will increase with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle s^{-2}} when we lower the energy-scale by s. At

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_D=\left(\frac{m}{M} \right)^{1/2}E_0 }

we find

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\Delta_{ij}(E_D)}{M}=\frac{\Delta_{ij}(E_0)}{M}\left(\frac{E_D}{E_0}\right)^{-2}=\frac{\Delta_{ij}}{m} }

that the restoring force is not suppressed anymore (m is small). Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_D} is the the Debye energy. This term is like a mass term, so below Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_D} the phonons will decouple. (There are two types of phonons in the crystall: acoustic and optical phonons. The latter occur when there are at least two types of ions per unit cell. In that case, the modes where the (oppositely charged) ions swing against each other is called optical because resulting time-varying electric dipole moment can be easily excited with IR radiation. The frequencies Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega(\mathbf{q})} of the optical modes are non-vanishing even as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{q}\to 0} . This is different for the acoustic modes, which correspond to the in-phase oscillations of the lattice iones. Those are in fact the Goldstone modes of the spontaneously broken translational symmetries, and Goldstone's theorem ensures that the eigenvalues of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta_{ij}(\mathbf{q})\to 0} and therefore Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega(\mathbf{q})\to 0} as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{q}\to 0} . As their creation has vanishing energy cost, there will be some acoustic phonons left even at arbitrarily small energies. However their effects are suppressed by phase space as well as by the fact that, as Goldstone bosons, their interactions are proportional to q.)

Fig 3: Scaling of the fermion-phonon interaction. Below Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_D } , the phonons decouple.

The interaction of fermions with phonons, i.e. one fermion absorbing or emitting a photon, is described by

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int d t d^3 \textbf{q} d^2 \textbf{k}_1 d \textbf{l}_1 d^2 \textbf{k}_2 d \textbf{l}_2 M^{-1/2} g_iD_i(\textbf{q})\psi^\dagger_\sigma(\textbf{p}_1)\psi_\sigma (\textbf{p}_2)\delta^3(\textbf{p}_1-\textbf{p}_2-\textbf{q}) }

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle g_i} in most generality is a function of the momenta Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle g_i=g_i(\textbf{q},\textbf{k}_1,\textbf{k}_2)} , but for simplicity take it to be just a simple constant. This scales as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle s^{-1+2-3/2}=s^{-1/2}} (the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta} -function does not scale because Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \textbf{q}} doesn't) and is relevant! When the phonons decouple at Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_D} , the dimensionless coefficient of fermion-phonon-interaction above, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle g_i\left(t\frac{m}{M}\right)^{1/2}} has grown to

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle g_i(E_D)\left(\frac{m}{M}\right)^{1/2}=g_i\left(\frac{E_D}{E_0}\right)^{-1/2}\left(\frac{m}{M}\right)^{1/2}=g_i\left(\frac{m}{M}\right)^{1/4} }

To proceed to energies below, we can integrate the phonons out. The emerging interaction then is again a 4-Fermi-term of the general form given at the beginning of the precious subsection 5.1. The scaling of this term also has been found in that subsection.

BCS-theory as consequence of interactions

Fig 3: Magnitude of the four-Fermi-interaction as function of the energy scale. The blue line shows the screend Coulomb interaction. The red line shows the Coulomb and Phonon interactions combined. There are two possibilities at low energy. To the left: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu^ast-\lambda>0} , the interaction scales to zero. To the right: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu^ast-\lambda<0} , lowering the energy scale eventually leads to the BCS instability.


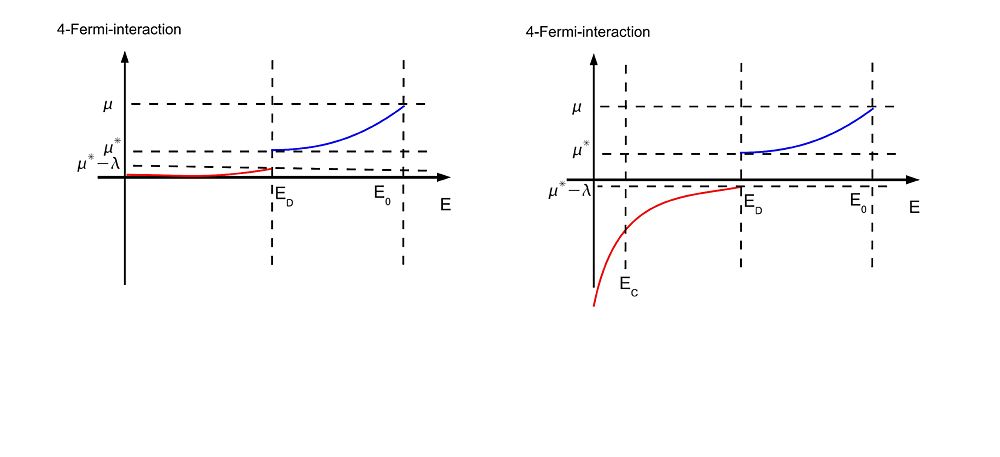
The emerging picture is the following. There are two kinds of four-Fermi-interactions in our system. One is the screened Coulomb interaction, which should be repulsive Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_C>0} . At energies below Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_D} , a new interaction Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_p} , obtained from integrating out phonons, enters the picture. This interaction is attractive Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_p<0} . Let's define Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu \equiv N V_c(E_0)} , then at Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_D} we find

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu^\ast = N V_c(E_D)=\frac{\mu}{1+\frac{\mu}{2}\ln (M/m)} }

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu^\ast<\mu} . Note that because of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle M/m \simeq 2000} , the logarithm in the denominator is quite large and therefore, no matter how big Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu^\ast\leq 0.2} . Equivalently to the definition of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu} , define for the four-Fermi-interactions from photon exchange, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda=-NV_p(E_D)} . The sign is chosen such that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda} is positive for attractive Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_p} . Just below Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_D} , the total four-fermi-interaction is

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle NV(E_1^-)=\mu^\ast-\lambda }

What happens next is depends on the sign of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu^\ast-\lambda} . If it is positive, the coupling will flow according to (\ref{eq:3dcoupling}) to smaller and smaller (positive) values as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E\to 0} . However if the total four-Fermi-interaction is attractive, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu^\ast-\lambda<0} , then the coupling flows to increasingly large negative values and will diverge at

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_c=E_De^{-1/(\lambda-\mu^\ast)}=E_0 \left( \frac{m}{M}\right)^{1/2}e^{-1/(\lambda-\mu^\ast)} }

The strong attractive interaction makes the fermions unstable, they condense into Cooper pairs, which breaks the electromagnetic U(1) symmetry and produces a gap. This is parallel to QCD, where at strong Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha_{\text{QCD}}} quark condensates form and break the chiral Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle SU(3)} . The prediction of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_c} should be taken - as all our the EFT results that are obtained from dimensional analysis- to be qualitative rather than quantitative. However it is a successs that we can predict BCS-condensation in the presence of screened Coulomb-repulsion. If we take Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda} to be of the same order, then superconductivity (that is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu^\ast-\lambda} being negative) seems quite likely, especially since Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu} decreases to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu^\ast} in the interval between Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_0} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_D} .

Isotope effect

Our approach yields a prediction for the isotope effect, i.e. the variation of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_c} (the critical temperature) with the ion mass M. We see that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_c} depends on M through the factor Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle M^{-1/2}} in the expression derived for the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_c} in the previous subsection but also implicitly by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu^\ast} , which depends on M. We find the exponent

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha =-\frac{M}{E_c}\partial_m E_c=\frac{1}{2} \left( 1- \frac{\mu^{\ast 2}}{(\lambda -\mu^\ast)^2}\right) }

While at first sight one would expect Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha=\frac{1}{2}} , we see that it can be substantially smaller if Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu^\ast} is not much less than Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda} . This is in fact observed in some materials, such as Mo, Os, Ru and Zr [4].

References

[1] R. Shankar "Renormalization-group approach to interaction fermions", Rev. Mod. Phys., Vol. 66, No. 1, 1994

[2] J. Polchinski "Effective field theory and the Fermi surface", arXiv [hep-th 9210046], 1992

[3] P. Coleman "Introduction to Many Body Physics", chap. 7, http://www.physics.rutgers.edu/~coleman/620/index.html\#monograph

[4] A. Bill, V.Z. Kresin, S.A. Wolf "The Isotope Effect in Superconductors", [arXiv: cond-mat/9801222v1]

Retrieved from "http://wiki.physics.fsu.edu/index.php?title=InteractingFermions&oldid=10194"