Wigner Crystallization: Difference between revisions
| Line 236: | Line 236: | ||
5. A. Mobius, and U. K. Rossler, Phys. Rev. B 79,174206 (2009) | 5. A. Mobius, and U. K. Rossler, Phys. Rev. B 79,174206 (2009) | ||
[http://wiki.physics.fsu.edu/wiki/index.php/Phy5670 Back to course page] | |||
Latest revision as of 16:54, 9 December 2010
Introduction
The study of electron transport is at the very heart of condensed matter physics. Band theory explains the physical properties of numerous materials, such as simple insulators, metals, and semiconductors. In metal, the electrons can move freely even at zero temperature because the conduction band is partially filled. On the other hand, insulators and semiconductor have fully filled valence band separated by an energy gap from an empty conduction band.
According to band theory, electrons in a perfectly periodic array of ions experience no collisions at all. However, some transition metal oxides with partially filled Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle d} or Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f} bands (predicted to be a metal) are poor conductors or even insulators. The reason for the absence of carrier mobility is electron localization. The first fundamental mechanism of electron localization is the random scattering of mobile electrons caused by impurities or defect (disorder), which is called Anderson localization. The transition from metal into insulator occurs when the mean free path becomes smaller than the De Broglie wavelength. Based on scaling theory of localization by Abraham, Anderson, et.al. , the metal-insulator transition (MIT) exists for non-interacting electrons in three dimensions (3D). In addition, the system is an insulator if the Fermi energy is smaller than the characteristic amplitude of the disorder potential. According to this theory, there is no true metallic behavior in two dimensions (2D) and one dimensions (1D) system with non interacting electron.
The second fundamental mechanism in MIT is caused by electron-electron interaction. One of the simplest examples for interaction driven localization is Wigner crystallization. In this system, each electron is confined not by an ionic potential, but due to the formation of a deep potential well produced by repulsion from other electrons embedded in a positive charge background.
The Jellium Model
The Hamiltonian of N electrons that interact with one another and with a uniform positive charge background is:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{H}=\hat{H}_{\mathrm{el}}+\hat{H}_{\mathrm{back}}+\hat{H}_{\mathrm{el-back}},\,}
where
- Hel is the electronic Hamiltonian consisting of the kinetic and electron-electron repulsion terms:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{H}_{\mathrm{el}}=\sum_{i=1}^N\frac{p_{i}^2}{2m}+\sum_{i<j}^N\frac{e^2}{|\mathbf{r}_i-\mathbf{r}_j|}}
- Hback is the Hamiltonian of the positive background charge interacting electrostatically with itself:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{H}_{\mathrm{back}}=\frac{e^2}{2}\int_{\Omega}\mathrm{d}\mathbf{R}\int_{\Omega}\mathrm{d}\mathbf{R}'\ \frac{n_b(\mathbf{R})n_b(\mathbf{R}')}{|\mathbf{R}-\mathbf{R}'|}}
- Hel-back is the electron-background interaction Hamiltonian, again an electrostatic interaction:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{H}_{\mathrm{el-back}}=\int_{\Omega}\mathrm{d}\mathbf{r}\int_{\Omega}\mathrm{d}\mathbf{R}\ \frac{n(\mathbf{r})n_b(\mathbf{R})}{|\mathbf{r}-\mathbf{R}|} }
- The electron number density operator:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{n}(\mathbf{r})=\sum_{i=1}^{N}\delta(\mathbf{r-r_{i}})}
- The uniform charge density of the background:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle en_{b}(\mathbf{r})=en} .
In other words, we replace the actual structure of the background on which the electrons live (e.g the atomic lattice) by homogeneous jelly-like continuum of positive charge background. Hence, we call it "Jellium model". We get rid of the complications associated with the structure of the host material, and only focus on the distinctive effects of the electron-electrons interaction. This model is very simplistic for traditional metallic systems, but it is quiet realistic in the semiconductor systems described in the next chapter.
If we do Fourier transform of the electronic density operator:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{n}_\mathbf{q}=\sum_{i=1}^{N}e^{-i\mathbf{q.r_i}}} ,
and the interaction potential
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle v_{\mathbf{q}}(\kappa)=\int v(\mathbf{r},\kappa)e^{-i\mathbf{q.r}}d\mathbf{r}} , where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \kappa^{-1}} is the regularization characteristic range by using Yukawa interaction as a tool and take the limit to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \kappa=0} after the end of calculation.
The expression of the potential in each dimensions are:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle v_{\mathbf{q}}=\begin{cases} \frac{4\pi e^{2}}{q^{2}} & 3D,\\ \frac{2\pi e^{2}}{q} & 2D, \textrm{and}\end{cases}}
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle v_{\mathbf{q}}(a)=-e^{2e^{q^{2}a^{2}}}Ei(-q^{2}a^{2})\quad1D.} ,
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Ei(x)} is the exponential-integral. In one dimension we use the trick by modelling the 1D system as an infinitely long 3D cylinder of small radius Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a} , hence the transverse motion of electrons is effectively "frozen" in the lowest energy state described by a Gaussian wave function[1]. These expression is useful to calculate the potential in such periodic structure where all the calculation is more efficient in momentum space
The Wigner Crystal
The Coulomb energy Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_{C}} is proportional to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1/a} , where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a} is the distance between the electrons. Hence, the Coulomb energy is proportional to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n^{1/d}} , where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n} is the density and d is the dimension of the system. The Fermi energy is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_{F}\sim n^{2/d}} , therefore Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r_{s}\sim n^{-1/d}} and at very low density , the electron can freeze and form a Wigner Crystal. A Wigner crystal (WC) is believed to be extremely fragile to both quantum and thermal fluctuations. To minimize the potential energy, the electrons form a triangular lattice (Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_{B}=-3.921\epsilon_{0}} ) in 2D, and BCC lattice in 3D, where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon_{0}=e^{2}/a} , and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a} is the nearest distance between electrons. It does not form a square lattice (Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_{B}=-3.900\epsilon_{0}} ) at zero temperature because of unstable shear modes in 2D systems. However, one cannot rule out the possibility that in some range of temperatures the square lattice (or other) is favored over the triangular lattice by entropy considerations [Maradudin&Bonsal]. As density increases, quantum fluctuation dominates the system. Above the critical density Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n_{c}} , a Wigner crystal cannot be found even at zero temperature.
When the density is very low, the distance between the electrons is sufficiently large. Hence, quantum effects are negligible and a classical approach can be applied. The values of the melting temperature Tc depend on the dimension, interaction range, and the filling factor. We can approach the continuum model by using a lattice model with very small filling.
We will review some known facts about Wigner crystallization for both classical and quantum systems. In classical models , the transition temperature Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_{C}} for short range interactions in lattice system (Ising model) is of the same order as the nearest neighbor (NN) interaction energy (Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_{C}=1.128} ) . The unit of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_{C}} is the coupling constant between nearest neighbors particles (Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle J/k_{B}} in Ising model and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e^{2}/k_{B}a} , where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle J} is Ising coupling, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k_{B}} is Boltzmann constant, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e} is electron charge, and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a} is the lattice size spacing). There are only a few models that have exact analytical solutions, such as 1D and 2D Ising models. Other models can only be solved numerically, e.g. 3D Ising model. For long range interaction, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_{C}} is one or two orders of magnitude lower than the nearest neighbor coupling . In a very early computer simulation, [S. G. Brush, H. L. Sahlin, E. Teller, J. Chem. Phys., 45,2102(1996)] observed a transition in a 32 particles continuum Coulomb gas model (Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Gamma_{c}\approx 125} ). The current estimate is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Gamma_{c}\sim172-178} in 3D Wigner crystal and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Gamma_{c}\sim125} in 2D Wigner crystal .
Experimental Support of Wigner crystallization
The picture of Wigner crystallization can be realized by ultra low density 2D electron or hole liquid in semiconductor devices. At the lowest density and the absence of disorder, one expects the electrons to freeze into a Wigner crystal, driving the system into an insulator. As we increase the density, the kinetic energy becomes sufficiently large, leading to the formation of a metal.
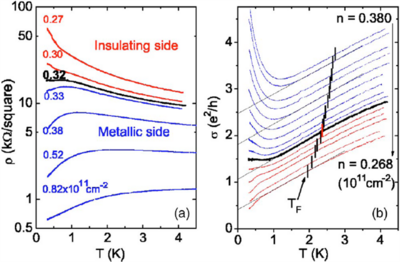
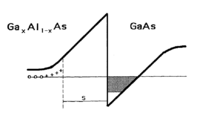
The samples consist of GaAs/AlGaAs or Si/SiGe heterojunction insulated-gate field-effect transistor (HIGFET) where the carriers are only capacitively induced by metal gate (figure 4.1). Two dimension electron gas (2DEG) is formed at GaAs and AlGaAs interface.
Typically, in these experiments, the Coulomb energy Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_{c}} is much larger than either thermal energy Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k_{b}T} (Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Gamma=E_{C}/k_{B}T\gg1} ) or Fermi energy Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_{F}} (), which means that strong e-e interaction dominates, bringing the system close to Wigner crystallization. Figure 4.2 shows a family curves of resistivity and conductivity as functions of temperature for several different carrier densities n. At low temperature, one observes a crossover from metallic behavior at high densities to insulating-like behavior as the density is reduced. At the lowest density, the unusual insulating-like behavior observed at all temperatures is remarkably weak; they observe an almost linear temperature dependence, in contrast to the conventional activated form observed in most insulators. Because the charge density is very low (small ), the zero point motion given by Fermi energy , where is the electron mass is very small and at finite temperature (T), the kinetic energy originates mainly from the classical thermal motion Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k_B T} . The melting of such a "classical" 2D eelctron solid is ditermined by only the competition between Coulomb interaction ()
The plausible origin of this unusual transport behavior is provided by simple estimates as shown by experimentalists [2]. First, they noted that the accessible temperature regime is typically above the temperature where one expects the melting of a Wigner crystal (less than 1 K), yet far below the typical Coulomb energy (>20K). These authors suggested that here one observes a strongly correlated liquid that can be described as an almost frozen Coulomb liquids. Second, this behavior persists far above the estimated Fermi energy, hence its origin is most likely of semi-classical character. Instead of the hard gap leading to the activated behavior ) in electronic spectrum expected for genuine Wigner crystal, here one expects a weak temperature dependence , with , which may reflect a formation of temperature dependent pseudogap.
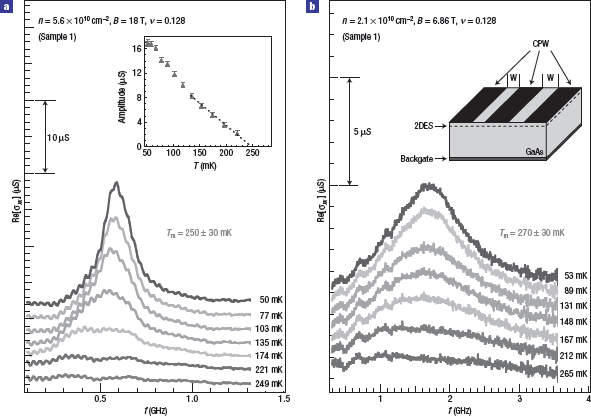
Another indirect evidence of Wigner crystallization is microwave resonance experiment in 2D semiconductor sample similar to the experiment above under a strong perpendicular magnetic field. At high enough magnetic field , it is well known that the kinetic energy suppressed and induce the crystallization. The melting temperature increases with the strength of the sample-dependence disorder that tends to pin the electron solid in phase [3]. The low energy excitations of Wigner crystal are quantized lattice vibrations (phonons) similar to those of an ordinary crystal. A spectrum of absorption produced when photon source (microwave) passes through a sample. The fraction of incident electromagnetic radiation will be absorbed by the material over a range of frequencies. They indirectly observed the formation of Wigner crystal from the microwave absorption spectrum (phonon excitation) at very low enough temperature in high magnetic field.
The Classical Monte Carlo Approach
To focus on the corresponding role of charge fluctuations, we deliberately ignore any spin effects, and consider a class of models of spinless electrons interacting through longrange interactions. We consider models given by the Hamiltonian:
where spinless electrons interact via a repulsive long-range potential of the form on a positive charge background for neutrality. Here, n is the occupation number of the lattice site (n=0 when there is no electron and n=1 when there is an electron on that site). We first examine in half-filled <n>=1/2 lattice where the system can be viewed as anti-ferromagnetic Ising model with the spin ).
- Classical Monte Carlo/Metropolis algorithm [4]
We use the simple Metropolis algorithm with Boltzmann statistics. Electric charge, lattice spacing, and dielectric constant are taken to be one to make the temperature T dimensionless. The system is a hypercubic half filled lattice with a fixed number of particles.
The metropolis algorithm steps include:
1. Choose an initial state with an electron on a site i
2. Calculate the resulting energy change if the electron Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e_{l}} move to a site j
3. Generate a random number Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r} such that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0<n_{r}<1}
4. If Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta E<} 0 or Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n_{r}<e^{-\Delta E/k_{b}T}} the movement is accepted
5. Go to the next electron Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e_{m}} and repeat the procedure.
In our simulation on half filled lattice, each movement in step 2 is only one site distant. If one uses lower filling factor in the lattice system, electron can jump over different distance.
Ewald Summation
We need a sufficiently large number of particles to get a reasonable simulation result of our finite systems. This finite-size effects can be reduced by imposing periodic boundary condition. Each particle interacts with other particles in the box and their images including its own images. Therefore, all boxes have the same configuration and we only need to calculate the dynamics in one box.
- Ewald summation to calculate potential from finite size system with periodic boundary condition
In the following we describe some technical details of the computational procedure used in Monte-Carlo simulations, in presence of long-range interactions. One of the main problems in any Monte Carlo simulations procedure is how to calculate the interaction energy with good accuracy and on a reasonable time scale. Our goal is to calculate electrostatic potential of point charges in the system. To deal with the electrostatic potential of periodic systems, we use Ewald summation. The Ewald summation is a technique for evaluating the potential, subject to periodic boundary condition, due to a lattice of point charges in a box plus a screening background. To illustrate the idea of Ewald summation, the electrostatic potential felt by a point charge (yellow particle on figure 3) caused by all other point charges (blue particles on figure 3) in one box and their images plus its own images is
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_{i}(\vec{r}_{i})=\acute{\sum_{j=1}}\sum_{n=0}\frac{e_{i}e_{j}}{|\vec{r}_{ij}+\vec{\mathbb{R}}_{n}|}} ,
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{r}_{ij}} is the distance between charge i and j in one box (simulation cell) and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{r}_{ij}+\vec{\mathbb{R}}_{n}} (Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \acute{\sum}_{j} } means Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i\ne j } when n=0) is the position of all the image charges including the image of charge i. In practice, we need to calculate the potential caused by a point charge at any distance \vec{r} in a simulation cell with its images in other cells (figure ewald). Therefore, the electrostatic energy caused by any pair of particles separated by the distance \vec{r} are known. For the illustration in a 1D picture (figure Ewald), first we observe the potential at the origin caused by an electron at position Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{r}} (red delta function) on the positive charge background (blue solid line).
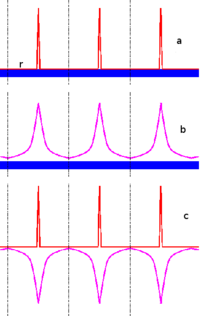
The charge density is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho_{a}} (Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{r}} )
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho_{a}(\vec{r})=\sum_{\vec{\mathbb{R}}_{n}}\delta(\vec{r}+\vec{\mathbb{R}}_{n})-\rho_{background},}
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{r}+\vec{\mathbb{R}}_{n}} ,n=0,1,2,... are positions of the point charge in the simulation cell and its images in other cells (figure 5.1.1a). It takes a very long time to accurately solve the Poisson equation
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \nabla^{2}\phi_{a}=-4\pi\rho_{a}} ,
due to above periodic charge density. The Ewald idea is to add normalized Gaussian distribution charge densities (plus and minus charges for neutrality) on top of the original charge density. This total charge density is split up into two components
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho_{b}(\vec{r})=(\varepsilon/\sqrt{\pi})\sum_{\mathbb{R}}e^{-\varepsilon(\vec{r}-\vec{\mathbb{R}}_{n})^{2}}-\rho_{background},} (figure 5.1.1b, )
and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho_{c}(\vec{r})=\sum_{\vec{\mathbb{R}_{n}}}\left(\delta(\vec{r}-\vec{\mathbb{R}}_{n})-\varepsilon/\sqrt{\pi}e^{-\varepsilon(\vec{r}-\vec{\mathbb{R}}_{n})}\right)} (figure 5.1.1c), where both have neutral total charge. The parameter Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \varepsilon^{-1/2}} is the width of the Gaussian charge density. Then we solve the Poisson equation from the charge distribution Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho_{b}} . Particularly in 3D, potential Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi_{b}} is a smooth function (Gaussian) in reciprocal/momentum space.
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi_{b}=\frac{4\pi}{\Omega}\sum_{\overrightarrow{k}\ne0}\frac{1}{k^{2}}e^{-k^{2}/4\varepsilon-i\overrightarrow{k}.\overrightarrow{r}},}
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Omega} is the volume of a unit cell and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{k}=2\pi\vec{n}/L} , where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{n}=\{n_{i},n_{j},n_{k}\},n_{i},n_{j},n_{k}} are integers. We do not include the value of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{k}=0} because the total charge in the system is zero. The Poisson equation with the charge density Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi_{c}} can be solved by integrating the Poisson equation over Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{r}} . The constant can be calculated and at the end the average potential in the super-cell is zero.
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi_{c}=\sum_{\vec{\mathbb{R}}_{n}}\frac{1-erf(\varepsilon|\vec{r}-\vec{\mathbb{R}}_{n}|)}{|\vec{r}-\vec{\mathbb{R}}_{n}|}-\frac{2\varepsilon}{\sqrt{\pi}},}
Parameter Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \varepsilon} determines how fast Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi_{b}} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi_{c}} converge. When Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \varepsilon} is large, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi_{b}} converges rapidly but Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi_{c}} converges slowly, and vice verse. Typically, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \varepsilon=\sqrt{\pi}} to get the same convergency rate in both potentials. With this technique, we can calculate and tabulate the electrostatic energy between 2 electrons separated by a distance \vec{r} and their images caused by periodic boundary condition with high accuracy for only two or three terms in the sums over of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{k}} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{\mathbb{R}}_{n}} . The total potential is just Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi_{Ewald}=\phi_{b} +\phi_{c}}
We use Ewald-type summation Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V(\vec{r}_{ij})} more general in any power of interaction Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1/r^\alpha} with the help of the integral representation of
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{|\vec{r}|^{\alpha}}=\frac{1}{\Gamma(\alpha/2)}\int_{0}^{\varepsilon}t^{\frac{\alpha}{2}-1}e^{-r^{2}t}dt+\int_{\varepsilon}^{\infty}t^{\frac{\alpha}{2}-1}e^{-r^{2}t}dt}
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Gamma(\alpha)} is Gamma function. We switch the first term of the integral to a momentum sum because the sum does not converge rapidly in the real space. Next, we use the representationwhere Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(\vec{r})} is any arbitrary function and on the right-hand side the summation is over the vectors of the reciprocal lattice. We then integrate out r and change the variable of the integration in the first term . The final expression of the potential takes the form Next, we use the representation:
- ,
where f(\vec{r}) is any arbitrary function and on the right-hand side the summation is over the vectors of the reciprocal lattice. We then integrate out r and change the variable of the integration in the first term t\rightarrow1/t. The final expression of the potential takes the form:
Simulation in half filled hypercubic Wigner crystal
Our results give support to the physical pictures of Wigner crystals proposed by experimentalists . The existence of an almost frozen liquid at proves to be a general phenomenon of any system with sufficiently long range interactions. We focus on the simplest possible models that can be studied in detail. Our system is a lattice gas model with Coulomb-like interactions in the form .
We consider models given by the Hamiltonian:
Hwhere spinless electrons interact via a repulsive long-range potential of the form
on a positive charge background for neutrality. Here, is the occupation number of the lattice site ( when there is no electron and n=1 when there is an electron on that site). We first examine in half-filled lattice where the system can be viewed as anti-ferromagnetic Ising model with the spin ).
- Classical Monte Carlo Simulation
We use the simple Metropolis algorithm with Boltzmann statistics. Electric charge, lattice spacing, and dielectric constant are taken to be one to make the temperature T dimensionless. The system is a hypercubic half filled lattice with a fixed number of particles.
The metropolis algorithm steps include:
1. Choose an initial state with an electron on a site i
2. Calculate the resulting energy change if the electron move to a site j
3. Generate a random number r such that
4. If or the movement is accepted
5. Go to the next electron and repeat the procedure.
In our simulation on half filled lattice, each movement in step 2 is only one site distant. If one uses lower filling factor in the lattice system, electron can jump over different distance.
- Simulation Steps
For N particles, one Monte Carlo time includes N metropolis cycles/updates. We use sequential updating rather than random updating to get smaller autocorrelation time [4].
A typical MC simulation consists of two parts:
1. Thermalization: Initial sweeps before the system reaches equilibrium state. There is no measurement during these sweeps.
2. Production: The system reaches equilibrium state and the measurements are performed.
The first step of the simulation is setting the initial condition. At low temperature, the system starts from crystallized condition (checkerboard pattern). At high temperature, the initial condition of the particles are randomly arranged. The decorrelation steps (purge sweeps between measurement) was performed to reduce the integrated autocorrelation time [4]. The autocorrelation function of any f is defined by:
- ,
the variance of f is a special case of autocorrelations . We need to calculate the autocorrelation time to determine the right error bar of any statistical parameter, , where the estimated uncorrelated random variables error bar (the central limit theorem), and is the integrated autocorrelation time, where
- .
Finite size effect and scaling
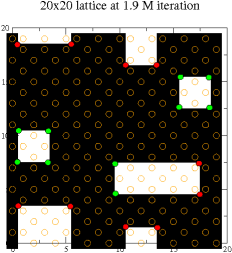
In a half filled lattice Coulomb gas model [5], the electrons form a checkerboard pattern in the ground state. We introduce an order parameter (staggered “magnetization”) to distinguish between the fluid (random) phase and the frozen (crystalline) phase. The order parameter is visualized in figure 5.2.1. In 2D, the order parameter ,where () the coordinate of the site i , and is the occupation number of site i. The circles are the electrons. Wide black or white area correspond to two different sublattices in their ground states which form checkerboard patterns. The total charge per unit cell at the corners of the domain walls (figure 5.2.1) between black and white areas are not neutral (yellow(+), red (-)).
When the system is in perfectly crystalline condition, the instaneous configuration of the order parameter will be either completely black or completely white, showing two different ground states. When the crystal melts, the black and white domains are distributed homogeneously with randomly arranged spins up and down. The thermalization time in a half filled lattice Coulomb gas model is much longer than for an Ising model, because of higher frustration (competition between different configurations). Typically, in a lattice size 30x30, the thermalization time in Ising model is 1000 times shorter than for a half filled lattice Coulomb gas model.
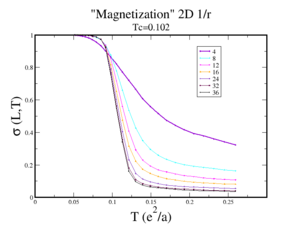
As we can see in figure 5.2.2 and 5.2.3, at low temperature, the average of absolute value of the order parameters is close to one and decrease rapidly at temperatures above T_{C}. The finite size effect can be clearly seen from observing how the the order parameter decreases above .
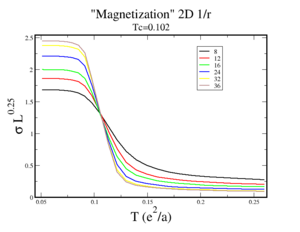
A study of finite size scaling consists of plotting the [Mobius,et.al], where is an anomalous dimension. All curves cross at Tc with the right estimate of . In this 2D system . The simulations show that critical exponents of half filled Coulomb lattice gas model is the same as that of nearest neighbor (NN) Ising model [5]. However, the interesting features of this system are in the intermediate regime when the crystal start to melt and forms a pseudogap state in a wide temperature range.
Classical Electron Liquid visualization
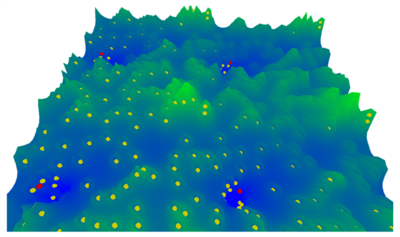
With this simple Jellium Model we can simulate classical Wigner crystal by decreasing the filling factor (number of electron over site). This website | (Java simulation of electron Liquid) by Eric Pelz shows how the filling factor change the critical temperature. Besides that, we can also add external electric field and impurities that can have positive and negative charges. In the algorithm, the change of energy of an electron by moving from position to is
- ,
where is the Coulomb energy of interaction between an electron with other electrons and impurities. The snapshot in figure [5.3.1] shows the potential surface with the electron(yellow balls) and impurities (redballs) at high enough temperature when electron can move freely. When the electrons bunch together, the potential surface is higher (brighter light) and electrons are surrounded by bowl-like equi-potential peaks reflecting no electron at the same site.
The Quantum Monte Carlo Approach
In this chaper we will discuss a brief review of some numerical solution with Quantum Monte Carlo (QMC) of electron liquid. It includes the effect of spins of electrons. The biggest question is at what value of the Wigner crystal form at certain temperature. Even at zero temperature, Wigner crystal phase will be not found if the value of is too small. Near the transition, the system is very far from both non interaction electron (small ) and classical Wigner crystal (big ). A technical breakthrough in 1980s, with the introduction of Quantum Monte Carlo (QMC) method, yielded highly accurate values for the ground-state energies of paramagnetic and spin polarized phases of the uniform electron liquid (Ceperly and Alder, 1980). But all we know today about the phase diagram of the electron liquid is based on the ground-state energies obtained from such calculation that still cannot determine the ground-state , but rather assume it from the start[1].
Variational Monte Carlo
In this approach , the expectation value of the hamiltonian in a trial wave function , where is spatial and spin coordinates of the N electrons.
is an upper bound to the ground-state energy based on Rayleigh-Ritz variational principle of quantum mechanics. To evaluate this integral, it uses a random walk to generate a set of points in configuration space. The main strangth of VMC method is in the fact that, through the choice of the trial wave function, it allows us to exert ingenuity and physical insight. Therefore, it will only be as good as the trial wave function one chooses. In addition, the variational energy is only sensitive to short-range correlations. Therefore, even with a fundamentally incorrect wave function, one can get very good values.
Diffusion Monte Carlo
The basic idea of diffusion monte carlo (DMC) is to let the initial wave funtion evolve in imaginary time according to the rule
- .
It will converge vor large to the true ground-state wave function as long as initial the wave function is chosen with a deliberate of ingenuity. The constant will be adjusted to keep the normalization constant and it will be the ground-state energy when this process is accomplished.
Path Integral Monte Carlo
Both VMC and DMC are instrinsically zero temperature methods. The path integral monte carlo (PIMC) method focuses on thermodynamic quantities which are obtained from the N-particle density matrix
- .
The evolution operator is in imaginary time. This approach doesn't rely on a trial wave function: it is calculated as a sum of probability amplitudes associated with paths (in configuration space ) that start at at , and return to ( permutation) at time . The PIMC method has great potential as a general purpose solver for many complex quantum mechanical system. Particularly, it can calculate the properties of energies of defects (interstitial and vacancies), melting temperature, and the effective interactions between spins in Wigner crystal.
The Phase Diagram of electron liquid
The calculation proposed by Perdew and Wang for the correlation energy of the three dimensional electron gas (in Rydberg per electron) based on the original QMC calculation of Ciperley and Alder:
where (ferromagnetic phase) , and (paramagnetic phase). The interpolation function so that , ,and . The spin-polarization dependence of the ground-state energy from this formula is not very accurate. The calculation of the p-dependence is difficult because the energy difference between state with different polarizations, systematic error affect the QMC results. The accuracy is increased by using twist-averaged boundary conditions instead of standard periodic ones. The tentative phase diagram of Jellium model is shown in figure 6.1.
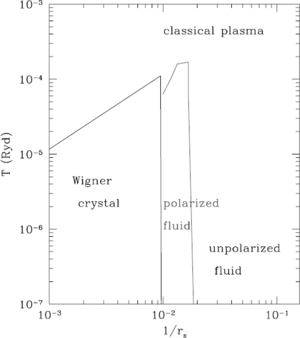
In 2D system, The ground state energy has been calculated by Tanatar and Ceperley in 1989, and in 2002 Attaccalite et al. A comparison between the energies on spin polarization and Wigner crystal at low density shows that the paramagnetic liquid is stable for , and the Wigner crystal has lower energy for . In the intermediate range , the problem is to date unsolved. It is very hard to decide which phase (paramagnetic and ferromagnetic liquid) has lower energy (Figure 6.2). The phase diagram of the electron liquid is till cannot completely understood even-though QMC method has provided very important result about relative stability of the simplest phases of the Jellium model. The occurrence of transtition between states of different symmetry indicates that the ground-state energy of the system is a nonanalytic function of , therefore it is conceptually incorrect to approximate it with an analytic function [1].
References
1. Gabriele Giuliani and Giovanni Vignale,"Quantum Theory of the Electron Liquid", Cambridge University Press (2005)
2. K. Lai, W. Pan, D. C. Tsui,at al.,Phys. Rev B,75,033314 (2007).
3. Piot, B.A.; Jiang, Z.; Dean, C.R., Engel, L.W., Gervais, G., Pfeiffer, L.N. and West, K.W., Nature Physics 4, 936 (2008)
4. Bernd A. Berg, Markov Chain and Monte Carlo Simulations and Their Statistical Analysis, (2004).
5. A. Mobius, and U. K. Rossler, Phys. Rev. B 79,174206 (2009)
















![{\displaystyle \int d^{d}r\sum _{\vec {n}}\delta ({\vec {r}}-[L{\vec {n}}+{\vec {r}}_{ij}])f({\vec {r}})=\int d^{d}r\sum _{{\vec {G}}_{l}}[e^{i{\vec {G}}_{l}.{\vec {r}}}-\delta ({\vec {r}})]f({\vec {r}})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dcd45eda5d7f289918d215176f99945f2ca1ecca)









































![{\displaystyle \epsilon _{c}^{(3D)}(r_{s},p)=\epsilon _{c}^{(3D)}(r_{s})+\alpha _{c}(r_{s}){\frac {f(p)}{f''(0)}}(1-p^{4})+\left[\epsilon _{c}^{(3D)}(r_{s},1)-\epsilon _{c}^{(3D)}(r_{s})\right]f(p)p^{4},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/20e955028eb046926fd6d7b72a752616ca0f1a2f)









