RGApproachToInteractingFermions

Introduction

The renormalization group (RG) is a very powerful tool in physics. Essentially, it is a way to continuously map a given theory onto other theories possessing the same low-energy physics by successively integrating out "fast", or high-energy, modes. This is expressed in terms of differential equations giving the "flows" of different coupling constants that appear in the theory. We are often interested in determining the fixed points of these flows, or points which these flows may end at, since these give us some important information about the system. For example, each fixed point corresponds to a certain phase of the system. Since there are many different sets of initial parameters that all flow to the same fixed point, we have an explanation of universality, or the observation that many different systems all possess similar physical properties, such as critical exponents [1]. Here, we will discuss how to perform RG for fermions, which differs in some respects from the case with bosonic fields. This discussion will follow that in Shankar's paper [1]. The most important difference, one which is true of any fermionic system, is that we have a Fermi sea in the ground state of our system. This means that, unlike in the bosonic case, we cannot simply impose a cutoff on the momentum, restricting it to the inside of a sphere of radius Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Lambda} . We will illustrate the correct procedure as we go along for different cases.

System at half-filling in one dimension

We will begin with a simple system - spinless ermions on a one-dimensional tight-binding lattice at half filling. The Hamiltonian for such a system without interactions is

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H_0=-t\sum_{\langle ij\rangle}\left (c^{\dagger}_{i+1} c_i+c^{\dagger}_i c_{i+1}\right ),}

where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle ij\rangle} means that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle j} are nearest neighbors, with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle j>i} . We can diagonalize this Hamiltonian by performing a Fourier transform, upon which we find that the energies are Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon(k)=-2t\cos{K}} , where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -\pi<K<\pi} . If we write the partition function for this Hamiltonian as a path integral, with the action written in momentum and frequency space, we get

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z_0=\int{D[\psi^{\ast},\psi] e^{-S_0}},}

where

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_0=\int_{-\infty}^{\infty}\frac{d\omega}{2\pi}\int_{-\pi}^{\pi}\frac{dK}{2\pi}\,\psi^{\ast}(K,\omega)(-i\omega-\cos{K})\psi(K,\omega).}

Note that we write an integral over the frequency, rather than a Matsubara sum; we are working at zero temperature, and will do so throughout this article. We have absorbed the constant Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t} into the field and frequency integral to bring our notation into contact with that of Shankar [1].

The RG transformation

We will now discuss how to perform RG for this system. First, we will find an RG transformation that will leave the above "bare" action invariant. We first impose a cutoff on the momentum integral. As noted before, we cannot simply restrict its range to a small region Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -\Lambda<K<\Lambda} due to the fact that the system's ground state is a filled Fermi sea. In this case, all states with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -\tfrac{\pi}{2}<K<\tfrac{\pi}{2}} are occupied. This means that our low-energy excitations are not excitations with small Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k} , but with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k} close to the Fermi surface. Therefore, our cutoff should restrict Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle K} to small regions around Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \pm\tfrac{\pi}{2}} . Let us define a new momentum Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k=|K|-\tfrac{\pi}{2}} . Since there are two regions that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle K} is restricted to, we will introduce a new label to our fields, specifying whether the momentum is near the left (Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -\tfrac{\pi}{2}} ) or the right (Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle +\tfrac{\pi}{2}} ) Fermi point. Since we are interested only in small Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k} , we will expand the energy to leading (in this case, linear) order. The action becomes

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_0=\sum_{i=L,R}\int_{-\infty}^{\infty}\frac{d\omega}{2\pi}\int_{-\Lambda}^{\Lambda}\frac{dk}{2\pi}\,\psi^{\ast}_i(k,\omega)(-i\omega+k)\psi_i(k,\omega),}

where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i} labels the "branch" of the Fermi surface, and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Lambda} is our cutoff.

We are now ready to begin finding the appropriate RG transformation. This is done in three steps [1]. First, we split the fields into "slow" (Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle \psi_{<}} ) and "fast" modes (Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle \psi_{>}} ) and integrate out the fast modes. The slow modes are defined over a range Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0\leq |k|\leq\tfrac{\Lambda}{s}} , where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle s>1} , and the fast modes are defined over Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tfrac{\Lambda}{s}\leq |k|\leq\Lambda} . We can then write Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle \psi_i(k,\omega)=\psi_{i,<}(k,\omega)+\psi_{i,>}(k,\omega)} . We will split the action into two parts - one containing only slow modes, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_{0,<}} and one containing only fast modes, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_{0,>}} . There are no terms mixing the two types of modes since they are defined on two disjoint intervals and both fields are at the same momentum. We can easily integrate out the fast modes since the integral is over a Gaussian, leaving just the slow modes. The result of the integration is just a constant, which we will drop. The action for the slow modes is thus

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_0=\sum_{i=L,R}\int_{-\infty}^{\infty}\frac{d\omega}{2\pi}\int_{-\Lambda/s}^{\Lambda/s}\frac{dk}{2\pi}\,\psi^{\ast}_{i,<}(k,\omega)(-i\omega+k)\psi_{i,<}(k,\omega).}

In order to compare this theory to other theories with the same cutoff, we must now rescale the momenta and frequencies to restore the momentum integral back to its original range [1]. To this end, let us define a new momentum Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k'=sk} and new frequency Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega'=s\omega} . Upon introducing these variables into the action, we obtain

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_0=\frac{1}{s^3}\sum_{i=L,R}\int_{-\infty}^{\infty}\frac{d\omega'}{2\pi}\int_{-\Lambda}^{\Lambda}\frac{dk'}{2\pi}\,\psi^{\ast}_{i,<}(\tfrac{k'}{s},\tfrac{\omega'}{s})(-i\omega'+k')\psi_{i,<}(\tfrac{k'}{s},\tfrac{\omega'}{s}).}

Finally, we rescale the fields so that the coefficient of some quadratic term in the action remains constant [1]. We define a new field Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi'_i(k',\omega')=\tfrac{1}{\zeta}\psi_{i,<}(\tfrac{k'}{s},\tfrac{\omega'}{s})} . We only have one quadratic term in our action, so we will leave its coefficient invariant. In terms of this new field, the action becomes

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_0=\frac{\zeta^2}{s^3}\sum_{i=L,R}\int_{-\infty}^{\infty}\frac{d\omega'}{2\pi}\int_{-\Lambda}^{\Lambda}\frac{dk'}{2\pi}\,{\psi'_i}^{\ast}(k',\omega')(-i\omega'+k')\psi'_i(k',\omega').}

If we define Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \zeta=\tfrac{1}{s^{3/2}}} , then we recover the original action in terms of rescaled variables.

We see that the three steps of the RG transformation we seek are: integrate out the fast modes, introduce rescaled momenta Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k'=sk} and frequencies Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega'=s\omega} , and introduce rescaled fields Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi'_i(k',\omega')=s^{3/2}\psi_{i,<}(\tfrac{k'}{s},\tfrac{\omega'}{s})} [1].

Quadratic perturbations

Now that we know the appropriate transformation, we may now look at how different perturbations scale under this transformation. Let us start with a quadratic perturbation. Our action with the perturbation becomes Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_0+\delta S_2} , where

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta S_2=-\sum_{i=L,R}\int_{-\infty}^{\infty}\frac{d\omega}{2\pi}\int_{-\Lambda}^{\Lambda}\frac{dk}{2\pi}\,\mu(k,\omega)\psi^{\ast}_i(k,\omega)\psi_i(k,\omega).}

We put a minus sign in this term to bring our sign convention in line with Shankar's [1]. Note that this perturbation preserves the symmetry between the two Fermi points. We now perform our RG transformation on this system. This separates directly into a piece depending only on the slow modes and one depending only on the fast modes, just as in the bare action. Therefore, when we integrate out the fast modes, we only generate a constant term in the action, which we drop. Performing the remaining two steps of the transformation, we obtain

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta S_2=-s\sum_{i=L,R}\int_{-\infty}^{\infty}\frac{d\omega'}{2\pi}\int_{-\Lambda}^{\Lambda}\frac{dk'}{2\pi}\,\mu(\tfrac{k'}{s},\tfrac{\omega'}{s}){\psi'_i}^{\ast}(k',\omega')\psi'_i(k',\omega'),}

We now expand the coupling function Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu} in a Taylor series [1],

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu(k,\omega)=\mu_{00}+\mu_{10}k+\mu_{01}i\omega+\cdots+\mu_{mn}k^m(i\omega)^n+\cdots.}

We may now determine how each of these terms scales with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle s} in the transformed action. In general, defining Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu'(k',\omega')=s\mu(\tfrac{k'}{s},\tfrac{\omega'}{s})} ,

$\mu '_{mn}={\frac {1}{s^{m+n-1}}}\mu _{mn}.$

We see that $\displaystyle \mu _{00}$ scales with a positive power of $s$, so that it grows as we increase $s$, and therefore integrate out more modes. Such a perturbation that grows under the RG transformation is called relevant [1]. As was guaranteed by our definition of the transformation, we find that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle \mu_{10}} and $\displaystyle \mu _{01}$ remain constant. Such perturbations are referred to as marginal [1]. Finally, if $m+n>1$, then $\displaystyle \mu _{mn}$ decreases under the RG transformation; these types of perturbations are referred to as irrelevant [1]. In all of our calculations, we will only retain terms in the action that are not irrelevant under the RG transformation.

Quartic perturbations

The scaling of quartic perturbations is not so trivial; in fact, these will lead to the flow equations for our system. The most general such perturbation, assuming a two-body interaction, is

$\delta S_{4}=-{\frac {1}{2!2!}}\int _{K\omega }u(4,3,2,1)\psi ^{\ast }(4)\psi ^{\ast }(3)\psi (2)\psi (1),$

where, following Shankar [1], we use the shorthand notation,

$\displaystyle \psi (i)=\psi (K_{i},\omega _{i})$

and

$\int _{K\omega }=\prod _{i=1}^{4}\left(\int _{-\pi }^{\pi }{\frac {dK_{i}}{2\pi }}\int _{-\infty }^{\infty }{\frac {d\omega }{2\pi }}\right)\times 2\pi {\bar {\delta }}(K_{1}+K_{2}-K_{3}-K_{4})\times 2\pi \delta (\omega _{1}+\omega _{2}-\omega _{3}-\omega _{4}),$

where ${\bar {\delta }}$ is a delta function that is infinite if its argument is zero modulo $2\pi$. Because the Grassman fields in the above perturbation are antisymmetric under the exchange of 1 and 2 or of 3 and 4, we require the same to be true of $u(4,3,2,1)$ [1]:

$\displaystyle u(4,3,2,1)=-u(4,3,1,2)=-u(3,4,2,1)=u(3,4,1,2)$

Even if Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u} had a symmetric part, it would be filtered out due to the antisymmetry under the exchange of the Grassman fields. Let us now rewrite this perturbation in terms of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k} and impose a cutoff on the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k} integrals. We get

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta S_4 = -\frac{1}{2!2!}\sum_{i_1,i_2,i_3,i_4=L,R}\int_{k\omega}^{\Lambda}u_{i_4 i_3 i_2 i_1}(4,3,2,1)\psi^{\ast}_{i_4}(4)\psi^{\ast}_{i_3}(3)\psi_{i_2}(2)\psi_{i_1}(1),}

where, again following Shankar [1], we write

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle \psi_{i_j}(j)=\psi_{i_j}(k_j,\omega_j)}

and

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int_{k\omega}^{\Lambda}=\prod_{i=1}^{4}\left (\int_{-\Lambda}^{\Lambda}\frac{dk_i}{2\pi}\int_{-\infty}^{\infty}\frac{d\omega}{2\pi}\right )\times 2\pi\bar{\delta}(k_1+k_2-k_3-k_4+(\epsilon_{i_1}+\epsilon_{i_2}-\epsilon_{i_3}-\epsilon_{i_4})\tfrac{\pi}{2})\times 2\pi\delta(\omega_1+\omega_2-\omega_3-\omega_4),}

where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon_i} is -1 if Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i=L} or +1 if Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i=R} . Let us consider all the possible values of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon_{i_1}+\epsilon_{i_2}-\epsilon_{i_3}-\epsilon_{i_4}} . The only possible values of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon_{i_1}+\epsilon_{i_2}} (and also Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon_{i_3}+\epsilon_{i_4}} ) are 2 (if both Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon} quantities are +1), 0 (if one is +1 and the other is -1), and -2 (if both are -1). This means that the only possible values of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon_{i_1}+\epsilon_{i_2}-\epsilon_{i_3}-\epsilon_{i_4}} are -4, -2, 0, +2, and +4. However, due to the fact that our Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k} variables are restricted to a region Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |k|\leq\Lambda} , with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Lambda} much smaller than Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tfrac{\pi}{2}} , we will never satisfy the restriction imposed by the delta function if Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon_{i_1}+\epsilon_{i_2}-\epsilon_{i_3}-\epsilon_{i_4}=\pm 2} . This means that we can only have couplings of the forms Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u_{LRLR}} and all couplings related to it by the above antisymmetry condition, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u_{LLRR}} , or Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u_{RRLL}} . This also means that we can eliminate the term containing the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon} quantities, which will make performing the RG transformation much easier.

Let us now apply the RG transformation to this term. Upon separating the fields into slow and fast modes, we note that, unlike the bare action and the quadratic perturbations, we cannot simply separate the quartic perturbation into a term with all slow modes and one with all fast modes. This is because, unlike in the quadratic case, our fields are not always at the same momentum because each field's momentum is integrated over separately. This allows for terms that mix slow and fast modes. Because of this, integrating out the fast modes is not a trivial task. One typically employs the cumulant expansion,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle e^{-\delta S}\rangle_{0,>} = \exp\left [-\langle \delta S\rangle_{0,>} +\tfrac{1}{2}\left (\langle (\delta S)^2\rangle_{0,>} -\langle \delta S\rangle^2_{0,>}\right )+\cdots\right ],}

and performs the integration perturbatively. Let us first consider the term containing all slow modes; this is known as the tree-level term [1].

Rescaling of the tree-level term

After carrying out the first step of our RG transformation, the tree-level term becomes

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta S_4 = -\frac{1}{2!2!}\sum_{i_1,i_2,i_3,i_4=L,R}\int_{k\omega}^{\Lambda/s}u(4,3,2,1)\psi^{\ast}_{i_4}(4)\psi^{\ast}_{i_3}(3)\psi_{i_2}(2)\psi_{i_1}(1).}

We introduce our rescaled variables as usual. We will pick up a factor of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (s^{3/2})^4=s^6} from rescaling the fields, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle s^{-8}} from the rescaling of the integration measures, and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle s^2} from the delta functions, since delta functions scale inversely with their arguments. Overall, this introduces no factors of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle s} , so that the new coupling function Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u'_{i_4 i_3 i_2 i_1}(k'_i,\omega'_i)} is

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u'_{i_4 i_3 i_2 i_1}(k'_i,\omega'_i)=u_{i_4 i_3 i_2 i_1}(\tfrac{k'_i}{s},\tfrac{\omega'_i}{s}).}

If we expand the above in powers of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k'} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega'} , we will find that the constant term is marginal and all higher-order terms are irrelevant. The constant term has further restrictions on the Fermi point labels due to all Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega} variables being zero. To be exact, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u_{LLRR}} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u_{RRLL}} must have zero constant terms. All that remains are Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u_{LRLR}} and the couplings related to it by permutations of the labels. We will thus label all of these as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u_{LRLR}=u_0} , and we will combine all of these terms together as one:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta S_4 = -u_0 \int_{k\omega}^{\Lambda}\psi^{\ast}_L(4)\psi^{\ast}_R(3)\psi_L(2)\psi_R(1).}

One-loop RG

Now we turn our attention to terms containing fast modes. This is where the above-mentioned cumulant expansion is used [1]. Let us begin with the first-order term in the expansion. The terms containing an odd number of fast modes will be zero, and the term containing all fast modes will simply give a constant, which we ignore. The only terms that give us any interesting non-zero contribution are those containing only two fast modes. There are, in fact, only two such terms. They are

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -u_0 \int_{k\omega}^{\Lambda}\langle \psi^{\ast}_{L,<}(4)\psi^{\ast}_{R,>}(3)\psi_{L,<}(2)\psi_{R,>}(1)\rangle_{0,>}}

and a similar term with both "L" fields being fast modes and both "R" fields being slow modes. These terms would introduce corrections to the quadratic terms,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta S_2=-\mu\sum_{i=L,R}\int_{-\infty}^{\infty}\frac{d\omega}{2\pi}\int_{-\Lambda}^{\Lambda}\frac{dk}{2\pi}\,\psi^{\ast}_i(k,\omega)\psi_i(k,\omega).}

Note that we dropped the subscript on Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu} .

Our original action, however, did not include a term of this form, and thus we must introduce one in order for there to be a non-trivial fixed point [1]. Let us suppose that we did have such a term, and see how it would rescale with this contribution added. We may write the above average as

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u_0 \int_{k\omega}^{\Lambda}\langle \psi^{\ast}_{R,>}(3)\psi_{R,>}(1)\rangle_{0,>}\psi^{\ast}_{L,<}(4)\psi_{L,<}(2).}

We can pull out the slow modes from the average because it is an average over only the fast modes. The average over two fields that is left is just a Green's function:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle \psi^{\ast}_{R,>}(3)\psi_{R,>}(1)\rangle_{0,>}=-2\pi\delta(\omega_3-\omega_1)\times2\pi\delta(k_3-k_1)G_R(k_1,\omega_1)}

Substituting in this result and eliminating all delta functions, we obtain

$-u_{0}\int _{-\infty }^{\infty }{\frac {d\omega _{2}}{2\pi }}\int _{-\Lambda /s}^{\Lambda /s}{\frac {dk_{2}}{2\pi }}\int _{-\infty }^{\infty }{\frac {d\omega _{1}}{2\pi }}\int _{\Lambda /s<|k|<\Lambda }{\frac {dk_{1}}{2\pi }}\,G_{R}(k_{1},\omega _{1})\psi _{L,<}^{\ast }(k_{2},\omega _{2})\psi _{L,<}(k_{2},\omega _{2}).$

We rescale the slow fields and the associated momenta and frequencies, obtaining

$-su_{0}\int _{-\infty }^{\infty }{\frac {d\omega '_{2}}{2\pi }}\int _{-\Lambda }^{\Lambda }{\frac {dk'_{2}}{2\pi }}\int _{-\infty }^{\infty }{\frac {d\omega _{1}}{2\pi }}\int _{\Lambda /s<|k|<\Lambda }{\frac {dk_{1}}{2\pi }}\,G_{R}(k_{1},\omega _{1}){\psi '_{L}}^{\ast }(k'_{2},\omega '_{2})\psi '_{L}(k'_{2},\omega '_{2}).$

Let us define

$\delta \mu =u_{0}\int _{-\infty }^{\infty }{\frac {d\omega _{1}}{2\pi }}\int _{\Lambda /s<|k|<\Lambda }{\frac {dk_{1}}{2\pi }}\,G_{R}(k_{1},\omega _{1}).$

We know that, at tree level, $\mu$ rescales as $\mu \rightarrow s\mu$. Therefore, putting all the pieces together, we find that, at one loop, the new quadratic coupling $\mu '$ is

$\mu '=s(\mu +\delta \mu )=s\left(\mu -u_{0}\int _{-\infty }^{\infty }{\frac {d\omega }{2\pi }}\int _{\Lambda /s<|k|<\Lambda }{\frac {dk}{2\pi }}\,{\frac {1}{i\omega -k}}\right).$

Here, we used the fact that the Green's function is just

$G_{R}(k,\omega )={\frac {1}{-i\omega +k}}.$

We now evaluate the integrals, starting with the frequency integral. To this end, we will introduce a small convergence factor, $\displaystyle e^{i\omega \eta }$, where $\eta$ is a small positive number that we take to zero at the end of our calculation. The frequency integral becomes

$\int _{-\infty }^{\infty }{\frac {d\omega }{2\pi }}\,{\frac {e^{i\omega \eta }}{i\omega -k}}.$

We may now evaluate the integral as a contour integral:

$\oint _{C}{\frac {d\omega }{2\pi }}\,{\frac {e^{i\omega \eta }}{i\omega -k}},$

where the contour $C$ is a semicircle whose straight-line base is on the real axis and the arc is in the half-plane where $\omega$ has a positive imaginary part. We may enlarge this semicircle to infinite radius. The arc gives zero contribution to the integral by Jordan's lemma since it decreases exponentially as the imaginary part of $\omega$ increases. Therefore, only the line contributes. The integrand has a pole at $\omega =-ik$. If $k$ is positive, then the pole lies outside the contour, and the integral is zero. If, on the other hand, $k$ is negative, then the pole is inside the contour, and we get a non-zero integral. The residue of this pole is $-i$, so the integral is given by

$\oint _{C}{\frac {d\omega }{2\pi }}\,{\frac {e^{i\omega \eta }}{i\omega -k}}=\theta (-k).$

Substituting this back into the equation for $\mu '$, we obtain

$\mu '=s(\mu +\delta \mu )=s\left(\mu -u_{0}\int _{\Lambda /s<|k|<\Lambda }{\frac {dk}{2\pi }}\,\theta (-k)\right)=s\left(\mu -u_{0}\int _{-\Lambda }^{-\Lambda /s}{\frac {dk}{2\pi }}\right)=s\left[\mu -{\frac {\Lambda u_{0}}{2\pi }}\left(1-{\frac {1}{s}}\right)\right].$

We may now derive the flow equation for this coupling constant. If we rearrange this equation, we will obtain, in terms of $\delta \mu =\mu '-\mu$,

$\delta \mu =(s-1)\left(\mu -{\frac {\Lambda u_{0}}{2\pi }}\right).$

Now, let $s=1+t$, where $t$ is infinitesimal. Then

${\frac {d\mu }{dt}}=\mu -{\frac {\Lambda u_{0}}{2\pi }}.$

One comment is in order. Typically, we wish to work at a fixed particle density. This means that we must hold the chemical potential constant. However, the above flow equation would imply that, in fact, the chemical potential changes. To counter this, we must change the bare chemical potential in such a way that, upon adding interactions, we are returned to the original value of the chemical potential [1]. The fixed point of this flow tells us how large a "counter term" we will need to add to keep the particle density fixed [1]. Before we can calculate this fixed point, we would need to know the flow equation for $u_{0}$ as well. We will derive this equation in the next section, and it will turn out that $u_{0}$ does not flow [1]. That is, we have a whole family of fixed points as a function of $u_{0}$. Therefore, $\mu$ at the fixed point is

$\mu ={\frac {\Lambda u_{0}}{2\pi }},$

or the point at which ${\tfrac {d\mu }{dt}}$ is zero.

Now we turn our attention to the second-order term in the cumulant expansion. This term will generate the one-loop corrections to the coupling $u_{0}$ [1]. We will find it convenient to think, to some degree, in terms of Feynman diagrams. Because of the linked-cluster theorem, we only need to consider connected diagrams. Let us first write down the general form of one of these second-order corrections:

$-{\tfrac {1}{2}}{\frac {1}{2!2!}}{\frac {1}{2!2!}}\int _{k\omega (8765)}^{\Lambda }\int _{k\omega (4321)}^{\Lambda }u(8,7,6,5)u(4,3,2,1)\langle \psi ^{\ast }(8)\psi ^{\ast }(7)\psi (6)\psi (5)\psi ^{\ast }(4)\psi ^{\ast }(3)\psi (2)\psi (1)\rangle _{0,>}$

Note that we used generic labels for all of the fields; this is because our arguments here will directly generalize to the other cases we will consider. All possible combinations of fast and slow fields will appear in this integral. However, we will only be interested in those terms that contain four slow modes and four fast modes. The others either give a constant, a two-loop correction to the quadratic coupling, or contribute to higher-order couplings. We will now use diagrams to help us visualize the different terms that will appear.

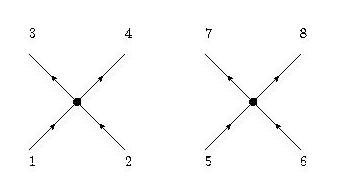
We will represent the two contributions as vertices with two "incoming" arrows to represent the $\psi ^{\ast }$ fields and two "outgoing" arrows to represent the $\psi$ fields:

Any line connecting two vertices in our diagrams will represent a Green's function, or a contraction. In our case, a fast mode (red line) must always be contracted with another fast mode, while slow modes (black lines) are never contracted. The momenta and frequencies of all lines entering and leaving a given vertex must be conserved.

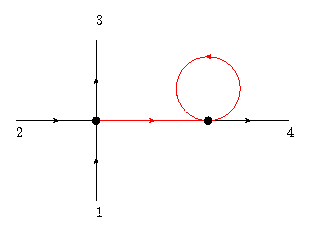
Let us consider a term that renormalizes the coupling $u(4,3,2,1)$. Such a term would have four slow modes with the specified attributes. We can now construct diagrams corresponding to different terms that could appear. As stated before, only connected diagrams need to be retained. We cannot make all four modes on one vertex fast and those on the other slow because this would result in a disconnected diagram. Next, we consider the case with all modes on one vertex slow except for one and all modes on the other vertex fast except for one. Such a diagram would look like this:

We can see that this will give no contribution as follows. On the right vertex, the momentum of the incoming fast mode is required to be equal to that of the outgoing slow mode, since the other two fast modes are contracted and thus must have the same momentum. This condition is impossible to satisfy.

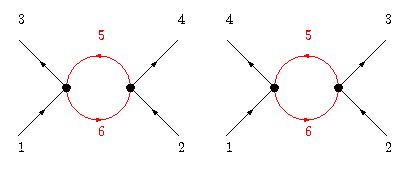
In fact, the only diagrams that will contribute are those in which each vertex has two fast modes and two slow modes. There are only two ways in which we may choose which lines are fast and which are slow. One way is to make one incoming line and one outgoing line on each diagram fast and the other two slow. For a correction to $u(4,3,2,1)$, we may either have 1 and 3 on one vertex and 2 and 4 on the other, or we may have 1 and 4 on one vertex and 2 and 3 on the other. The corresponding diagrams are shown below.

The labels, 5 and 6, on the fast modes refer to formulas that we will derive below. Following Shankar, we will refer to the left diagram as the ZS diagram and the right diagram as the ZS' diagram [1].

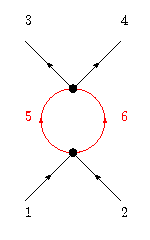
Another possibility would be to make both incoming lines on one vertex and both outgoing lines on the other vertex slow. This would correspond to the following diagram:

Again following Shankar, we will refer to this diagram as the BCS diagram [1].

Let us now determine the contributions from each diagram. First, we consider the ZS diagram. Before writing down its contribution, we must first determine how many different ways we can construct the diagram. There are four ways we could have chosen which lines were slow on each vertex - two choices for the incoming line and two for the outgoing line. It also doesn't matter which vertex we associate 1 and 3 with, so this gives us another factor of two. Overall, this gives $4^{2}\times 2=32$ different ways to choose these lines. Each of the terms these would correspond to can be made identical by a relabeling and permutation of the lines. Overall, the contribution from the ZS diagram is

$-\int _{k\omega (8472)}^{\Lambda }\int _{k\omega (6351)}^{\Lambda }u(8,4,7,2)u(6,3,5,1)\langle \psi _{>}^{\ast }(8)\psi _{<}^{\ast }(4)\psi _{>}(7)\psi _{<}(2)\psi _{>}^{\ast }(6)\psi _{<}^{\ast }(3)\psi _{>}(5)\psi _{<}(1)\rangle _{0,>}.$

If we pull out the slow modes from the average, we get

$\int _{k\omega (8472)}^{\Lambda }\int _{k\omega (6351)}^{\Lambda }u(8,4,7,2)u(6,3,5,1)\langle \psi _{>}^{\ast }(8)\psi _{>}(7)\psi _{>}^{\ast }(6)\psi _{>}(5)\rangle _{0,>}\psi _{<}^{\ast }(4)\psi _{<}^{\ast }(3)\psi _{<}(2)\psi _{<}(1).$

To facilitate the following calculations, we will explicitly write out the integrals:

$\prod _{i=5}^{8}\left(\int _{-\infty }^{\infty }{\frac {d\omega _{i}}{2\pi }}\int _{\text{fast}}{\frac {dk_{i}}{2\pi }}\right)\prod _{i=1}^{4}\left(\int _{-\infty }^{\infty }{\frac {d\omega _{i}}{2\pi }}\int _{\text{slow}}{\frac {dk_{i}}{2\pi }}\right)u(8,4,7,2)u(6,3,5,1)\langle \psi _{>}^{\ast }(8)\psi _{>}(7)\psi _{>}^{\ast }(6)\psi _{>}(5)\rangle _{0,>}\psi _{<}^{\ast }(4)\psi _{<}^{\ast }(3)\psi _{<}(2)\psi _{<}(1)(2\pi )^{2}\delta (8+4-7-2)(2\pi )^{2}\delta (6+3-5-1),$

where the delta functions shown here represent the delta function factors that enforce conservation of momentum and frequency.

Performing the rescaling of the momenta, frequencies, and fields for the slow modes, this becomes

$\prod _{i=5}^{8}\left(\int _{-\infty }^{\infty }{\frac {d\omega _{i}}{2\pi }}\int _{\text{fast}}{\frac {dk_{i}}{2\pi }}\right)\prod _{i=1}^{4}\left(\int _{-\infty }^{\infty }{\frac {d\omega '_{i}}{2\pi }}\int _{\text{slow, rescaled}}{\frac {dk'_{i}}{2\pi }}\right)u(8,4,7,2)u(6,3,5,1)\langle \psi _{>}^{\ast }(8)\psi _{>}(7)\psi _{>}^{\ast }(6)\psi _{>}(5)\rangle _{0,>}{\psi '}^{\ast }(4){\psi '}^{\ast }(3)\psi '(2)\psi '(1)(2\pi )^{2}\delta (8+4-7-2)(2\pi )^{2}\delta (6+3-5-1).$

We now use Wick's theorem to evaluate the average. The only way to contract the fields that results in a connected diagram is to contract 8 with 5 and 7 with 6. The result of this is

$-\prod _{i=5}^{8}\left(\int _{-\infty }^{\infty }{\frac {d\omega _{i}}{2\pi }}\int _{\text{fast}}{\frac {dk_{i}}{2\pi }}\right)\prod _{i=1}^{4}\left(\int _{-\infty }^{\infty }{\frac {d\omega '_{i}}{2\pi }}\int _{\text{slow, rescaled}}{\frac {dk'_{i}}{2\pi }}\right)u(8,4,7,2)u(6,3,5,1)G(5)G(6){\psi '}^{\ast }(4){\psi '}^{\ast }(3)\psi '(2)\psi '(1)(2\pi )^{2}\delta (8+4-7-2)(2\pi )^{2}\delta (8-5)(2\pi )^{2}\delta (7-6)(2\pi )^{2}\delta (6+3-5-1).$

We now eliminate delta functions to obtain

$-\prod _{i=5}^{6}\left(\int _{-\infty }^{\infty }{\frac {d\omega _{i}}{2\pi }}\int _{\text{fast}}{\frac {dk_{i}}{2\pi }}\right)\prod _{i=1}^{4}\left(\int _{-\infty }^{\infty }{\frac {d\omega '_{i}}{2\pi }}\int _{\text{slow, rescaled}}{\frac {dk'_{i}}{2\pi }}\right)u(5,4,6,2)u(6,3,5,1)G(5)G(6){\psi '}^{\ast }(4){\psi '}^{\ast }(3)\psi '(2)\psi '(1)(2\pi )^{2}\delta (6+3-5-1)(2\pi )^{2}\delta (4+3-2-1).$

We now have the expression in a form in which it is clear that it is a renormalization of $u$. The contribution from this term is

${\text{ZS}}=\int d5\,\int d6\,u(5,4,6,2)u(6,3,5,1)G(5)G(6)(2\pi )^{2}\delta (6+3-5-1),$

where, following Shankar [1], we adopt the shorthand notation,

$\int di,$

to represent an integral over "fast" momenta and frequencies.

We may obtain the ZS' term by simply interchanging 3 and 4 in the above calculation. The result is

${\text{ZS}}'=-\int d5\,\int d6\,u(5,3,6,2)u(6,4,5,1)G(5)G(6)(2\pi )^{2}\delta (6+4-5-1),$

where the extra minus sign is due to the fact that we will have to swap the $\psi ^{\ast }(4)$ and $\psi ^{\ast }(3)$ fields.

Now we turn our attention to the BCS diagram. In this case, we may choose either vertex to "carry" the incoming slow modes. Once we decide on which vertex "carries" them, we may arrange the slow modes two ways. The same holds true for the other vertex, which must "carry" the fast modes. Overall, there are $2^{3}=8$ different ways to choose these lines. The overall contribution from the BCS diagram is then

$-{\tfrac {1}{4}}\int _{k\omega (4387)}^{\Lambda }\int _{k\omega (6521)}^{\Lambda }u(4,3,8,7)u(6,5,2,1)\langle \psi _{<}^{\ast }(4)\psi _{<}^{\ast }(3)\psi _{>}(8)\psi _{>}(7)\psi _{>}^{\ast }(6)\psi _{>}^{\ast }(5)\psi _{<}(2)\psi _{<}(1)\rangle _{0,>}.$

Pulling out the slow modes from the average, we get

$-{\tfrac {1}{4}}\int _{k\omega (4387)}^{\Lambda }\int _{k\omega (6521)}^{\Lambda }u(4,3,8,7)u(6,5,2,1)\langle \psi _{>}(8)\psi _{>}(7)\psi _{>}^{\ast }(6)\psi _{>}^{\ast }(5)\rangle _{0,>}\psi _{<}^{\ast }(4)\psi _{<}^{\ast }(3)\psi _{<}(2)\psi _{<}(1),$

or, explicitly writing out the integrals,

$-{\tfrac {1}{4}}\prod _{i=5}^{8}\left(\int _{-\infty }^{\infty }{\frac {d\omega _{i}}{2\pi }}\int _{\text{fast}}{\frac {dk_{i}}{2\pi }}\right)\prod _{i=1}^{4}\left(\int _{-\infty }^{\infty }{\frac {d\omega _{i}}{2\pi }}\int _{\text{slow}}{\frac {dk_{i}}{2\pi }}\right)u(4,3,8,7)u(6,5,2,1)\langle \psi _{>}(8)\psi _{>}(7)\psi _{>}^{\ast }(6)\psi _{>}^{\ast }(5)\rangle _{0,>}\psi _{<}^{\ast }(4)\psi _{<}^{\ast }(3)\psi _{<}(2)\psi _{<}(1)(2\pi )^{2}\delta (4+3-8-7)(2\pi )^{2}\delta (6+5-2-1).$

We now rescale the momenta, frequencies, and fields for the slow modes, obtaining

$-{\tfrac {1}{4}}\prod _{i=5}^{8}\left(\int _{-\infty }^{\infty }{\frac {d\omega _{i}}{2\pi }}\int _{\text{fast}}{\frac {dk_{i}}{2\pi }}\right)\prod _{i=1}^{4}\left(\int _{-\infty }^{\infty }{\frac {d\omega '_{i}}{2\pi }}\int _{\text{slow, rescaled}}{\frac {dk'_{i}}{2\pi }}\right)u(4,3,8,7)u(6,5,2,1)\langle \psi _{>}(8)\psi _{>}(7)\psi _{>}^{\ast }(6)\psi _{>}^{\ast }(5)\rangle _{0,>}{\psi '}_{<}^{\ast }(4){\psi '}_{<}^{\ast }(3)\psi '_{<}(2)\psi '_{<}(1)(2\pi )^{2}\delta (4+3-8-7)(2\pi )^{2}\delta (6+5-2-1).$

We now evaluate the average over fast modes. This time, however, there are two ways to contract the fields and obtain a connected diagram. We may contract 8 with 5 and 7 with 6, or contract 8 with 6 and 7 with 5. Both contributions can be made identical by a simple relabeling and permutation of the fields and arguments of $u$. We obtain, after eliminating the delta functions coming from the contractions,

${\tfrac {1}{2}}\prod _{i=5}^{6}\left(\int _{-\infty }^{\infty }{\frac {d\omega _{i}}{2\pi }}\int _{\text{fast}}{\frac {dk_{i}}{2\pi }}\right)\prod _{i=1}^{4}\left(\int _{-\infty }^{\infty }{\frac {d\omega '_{i}}{2\pi }}\int _{\text{slow, rescaled}}{\frac {dk'_{i}}{2\pi }}\right)u(4,3,6,5)u(6,5,2,1)G(5)G(6){\psi '}_{<}^{\ast }(4){\psi '}_{<}^{\ast }(3)\psi '_{<}(2)\psi '_{<}(1)(2\pi )^{2}\delta (6+5-2-1)(2\pi )^{2}\delta (4+3-2-1).$

Again, we have reduced the expression to a form in which it is obvious that it contributes to the renormalization of $u$. The contribution from this term is thus

${\text{BCS}}=-{\tfrac {1}{2}}\int d5\,\int d6\,u(4,3,6,5)u(6,5,2,1)G(5)G(6)(2\pi )^{2}\delta (6+5-2-1).$

The total correction to $u(4,3,2,1)$ is thus

$\displaystyle \delta u(4,3,2,1)={\text{ZS}}+{\text{ZS}}'+{\text{BCS}}.$

This is the "master formula" stated by Shankar; as stated earlier, it may easily be generalized to higher dimensions [1]. In fact, we used labels such as "fast" to denote the momentum integration limits rather than specific values of the momentum in order to emphasize that nothing in this derivation relied on us working with any specific system.

We will now apply this formula to the current system. As usual, we will consider a vertex with all momenta on the Fermi surface and with all frequencies set to zero, because this is the only quartic coupling that is not irrelevant under the RG transformation [1]. This means that, similarly, all of the slow modes will be placed on the Fermi surface with their frequencies set to zero. Due to conservation of the frequencies at each vertex, we see that, in the ZS and ZS' diagrams, the frequencies of the fast modes must be equal, while those on the BCS diagram are equal in magnitude and opposite in sign. We now determine the allowed momenta for the fast modes. The range that our momenta are restricted to is shown below (figure reproduced from Shankar [1]):

The thick lines labeled "a", "b", "c", and "d" are the regions to which the momenta of the fast modes are restricted.

Let us consider the renormalization of $u_{LRLR}$, so that the momenta of 1 and 3 are both at R, and those of 2 and 4 are at L. We will now work out what the momenta of 5 and 6 should be so that the momenta are conserved modulo $2\pi$ for each diagram. We will consider the ZS diagram first. Let the momentum of 5 be $K$ (this is the total momentum, not the deviation of the momentum from the Fermi surface). Since the momenta of 1 and 3 are both at R, this means that the momenta of 5 and 6 must be equal; that is, the momentum of 6 is also $K$. The ZS contribution to the renormalization is then, inserting the expression for the Green's function and eliminating the delta functions,

${\text{ZS}}=\int _{-\infty }^{\infty }{\frac {d\omega }{2\pi }}\int _{d\Lambda }{\frac {dk}{2\pi }}\,u(K,L,K,L)u(K,R,K,R){\frac {1}{-i\omega +E(K)}}{\frac {1}{-i\omega +E(K)}},$

where the $d\Lambda$ means that the momentum $K$ must lie in one of the four regions a, b, c, and d shown in the above figure.

Next, we consider the ZS' diagram. Since the momentum of 1 is at R and that of 4 is at L, this means that, if the momentum of 5 is $K$, then that of 6 must be $K+\pi$, since the momentum of 4 is less than that of 1 by $\pi$. Using the fact that the energy, $E(K)=-\cos {K}$, has the property that $E(K+\pi )=-E(K)$, we obtain for the ZS' contribution

${\text{ZS}}'=-\int _{-\infty }^{\infty }{\frac {d\omega }{2\pi }}\int _{d\Lambda }{\frac {dk}{2\pi }}\,u(K,R,K+\pi ,L)u(K+\pi ,L,K,R){\frac {1}{-i\omega +E(K)}}{\frac {1}{-i\omega -E(K)}}.$

Finally, we look at the BCS diagram. Since the momentum of 1 is R and that of 2 is L, this means that, if the momentum of 5 is $K$, then that of 6 must be $-K$. We note that $E(-K)=E(K)$, so that the BCS contribution becomes

${\text{BCS}}=-{\tfrac {1}{2}}\int _{-\infty }^{\infty }{\frac {d\omega }{2\pi }}\int _{d\Lambda }{\frac {dk}{2\pi }}\,u(L,R,-K,K)u(-K,K,L,R){\frac {1}{-i\omega +E(K)}}{\frac {1}{i\omega +E(K)}}.$

Let us now evaluate each contribution, starting with the ZS diagram. We may see immediately upon considering the frequency integral that this contribution is zero. This is because both poles of the integral lie on the same side of the real axis in the complex plane. If we use the trick of rewriting the integral as a contour integral over an infinite semicircle, then we may close the contour on the side of the complex plane that does not contain the poles. Since the integrand goes as ${\tfrac {1}{\omega ^{2}}}$, the contribution from the semicircular arc is zero by Jordan's lemma. Therefore, the frequency integral is zero.

Next, we consider the ZS' contribution. In this case, the poles of our integrand are on opposite sides of the real axis. This means that the integral does not vanish as it did in the ZS case. Let us close the contour on the side of the complex plane in which the imaginary part of $\omega$ is positive. Evaluating this integral gives us

${\text{ZS}}'={\frac {1}{4\pi }}\int _{d\Lambda }dk\,u(K,R,K+\pi ,L)u(K+\pi ,L,K,R){\frac {1}{|E(K)|}}.$

In order to obtain a non-zero value for $u(K+\pi ,L,K,R)$ to constant order, we must have $K$ near L, and therefore $K+\pi$ will be near R. Replacing $E(K)$ with its expression in terms of $k$, we obtain

${\text{ZS}}'={\frac {1}{4\pi }}\int _{d\Lambda }dk\,u_{LRRL}u_{RLLR}{\frac {1}{|k|}}.$

By definition, $u_{LRRL}=u_{RLLR}=-u_{0}$, so

${\text{ZS}}'={\frac {u_{0}^{2}}{4\pi }}\int _{d\Lambda }dk\,{\frac {1}{|k|}}.$

Since $K$ was restricted to be near R (that is, in c or d), these are the only two regions we need to integrate over. Doing so, we obtain

${\text{ZS}}'={\frac {u_{0}^{2}}{2\pi }}\ln {s}.$

Finally, we consider the BCS diagram. By a similar argument to the ZS' case, we may evaluate the frequency integral to obtain

${\text{BCS}}=-{\frac {1}{8\pi }}\int _{d\Lambda }dk\,u(L,R,-K,K)u(-K,K,L,R){\frac {1}{|k|}}.$

In this case, there are no other restrictions on $K$ other than that it must lie in one of the regions a, b, c, or d. The contribution for which $K$ is near R is

$-{\frac {1}{8\pi }}\int _{\Lambda /s<|k|<\Lambda }dk\,u(L,R,L,R)u(L,R,L,R){\frac {1}{|k|}},$

while those in which $K$ is near L are

$-{\frac {1}{8\pi }}\int _{\Lambda /s<|k|<\Lambda }dk\,u(L,R,R,L)u(R,L,L,R){\frac {1}{|k|}}.$

These two contributions, however, are completely identical. Therefore, the total BCS contribution is given by

${\text{BCS}}=-{\frac {u_{0}^{2}}{2\pi }}\ln {s}.$

This exactly cancels the ZS' contribution, so that the total change in $u$ is

$\displaystyle \delta u_{0}=0.$

We have thus shown that, to one loop, $u_{0}$ does not flow; in other words,

${\frac {du_{0}}{dt}}=0.$

Interpretation of results

Let us attach some physical context to these results. Suppose that the quartic coupling were a nearest-neighbor interaction, whose Hamiltonian is given by

$H_{I}=U_{0}\sum _{\langle ij\rangle }c_{j}^{\dagger }c_{i}^{\dagger }c_{i}c_{j},$

or

$H_{I}=U_{0}\sum _{j}c_{j+1}^{\dagger }c_{j}^{\dagger }c_{j}c_{j+1}.$

We will now Fourier transform this interaction. First, we introduce the operators,

$c_{j}=\int _{-\pi }^{\pi }{\frac {dK}{2\pi }}\,e^{iKj}c(K),$

obtaining

$H_{I}=U_{0}\prod _{j=1}^{4}\left(\int _{-\pi }^{\pi }{\frac {dK_{j}}{2\pi }}\right)\sum _{j}c^{\dagger }(K_{4})c^{\dagger }(K_{3})c(K_{2})c(K_{1})e^{i(K_{1}-K_{4})}e^{i(K_{1}+K_{2}-K_{3}-K_{4})j}.$

Using the result that

$H_{I}=\sum _{j}e^{i(K_{1}+K_{2}-K_{3}-K_{4})j}=2\pi {\bar {\delta }}(K_{4}+K_{3}-K_{2}-K_{1}),$

this becomes

$H_{I}=U_{0}\prod _{j=1}^{4}\left(\int _{-\pi }^{\pi }{\frac {dK_{j}}{2\pi }}\right)2\pi {\bar {\delta }}(K_{4}+K_{3}-K_{2}-K_{1})c^{\dagger }(K_{4})c^{\dagger }(K_{3})c(K_{2})c(K_{1})e^{i(K_{1}-K_{4})}.$

Since this expression is antisymmetric under the exchange of $c(K_{1})$ and $c(K_{2})$, as well as under the exchange of $c^{\dagger }(K_{3})$ and $c^{\dagger }(K_{4})$, we may rewrite the above as

$H_{I}=-{\tfrac {1}{4}}\prod _{j=1}^{4}\left(\int _{-\pi }^{\pi }{\frac {dK_{j}}{2\pi }}\right)2\pi {\bar {\delta }}(K_{4}+K_{3}-K_{2}-K_{1})u(K_{4},K_{3},K_{2},K_{1})c^{\dagger }(K_{4})c^{\dagger }(K_{3})c(K_{2})c(K_{1}),$

where $u(K_{4},K_{3},K_{2},K_{1})$ is the completely antisymmetric function,

$u(K_{4},K_{3},K_{2},K_{1})=U_{0}\left[e^{i(K_{1}-K_{3})}-e^{i(K_{1}-K_{4})}-e^{i(K_{2}-K_{3})}+e^{i(K_{2}-K_{4})}\right].$

This corresponds exactly to the quartic perturbation we used in our RG analysis above. Let us now determine the lowest-order terms in $k$ in two cases. First, we consider the case where $K_{1}$ and $K_{3}$ are near R, and the others near L. Then

$u(K_{4},K_{3},K_{2},K_{1})=U_{0}\left[e^{i(k_{1}-k_{3})}+e^{i(k_{1}+k_{4})}+e^{i(-k_{2}-k_{3})}+e^{i(-k_{2}+k_{4})}\right]\approx 4U_{0}.$

This coupling, which would correspond to our $u_{LRLR}$, is therefore constant at lowest order, and would be marginal under our RG transformation.

Let us also consider the case in which $K_{1}$ and $K_{2}$ are near R, and the others near L. This would correspond to umklapp scattering. Then

$u(K_{4},K_{3},K_{2},K_{1})=-U_{0}\left[e^{i(k_{1}+k_{3})}-e^{i(k_{1}+k_{4})}-e^{i(k_{2}+k_{3})}+e^{i(k_{2}+k_{4})}\right]\approx U_{0}(k_{1}-k_{2})(k_{3}-k_{4}).$

Therefore, at lowest order, this coupling, which would correspond to $u_{LLRR}$, is quadratic in $k$, and would be irrelevant under our RG transformation.

The Hamiltonian with this perturbation added, which would give us a Hubbard model for spinless fermions, has been solved exactly by Yang and Yang [2]. In reality, they solve the problem of a 1-D chain of interacting spins, but their solution can be mapped onto this problem via a Jordan-Wigner transformation [1] [2]. In their solution, they find that our system will undergo a phase transition into a charge density wave (CDW) state when the interaction is repulsive and ${\tfrac {U_{0}}{t}}$ is of order one [1] [2]. In other words, our system will not immediately collapse into a CDW state for an infinitesimal interaction. This conclusion agrees with the results we find from our RG analysis above. We considered small perturbations about a non-interacting tight-binding model in one dimension at half-filling. However, let us suppose that we did not treat the non-interacting system as our "base" system, but rather an interacting system. If we carry out the analysis leading to the RG transformation as before, we will find that the different perturbations rescale differently under the new RG transformation. In particular, the $u_{LLRR}$ terms which, to lowest order, were quadratic in $k$, will eventually become relevant if we increase the "base" value of $U_{0}$ to a large enough value [1].

In principle, simply deriving the flow equations on their own is not enough to conclude anything about what phase the system will enter. We will need some other means of making this decision. One method would be to calculate the susceptibilities for all possible observables related to the system to an appropriate order in the perturbations and compare them. If the system is unstable to the corresponding ordered phase, then the appropriate susceptibility will diverge. For example, if the system is unstable to antiferromagnetic order, then the susceptibility for the staggered magnetization will diverge. If there are multiple such susceptibilities, then the one that diverges most rapidly is assumed to "win", and therefore we conclude that the system enters that phase. This is done, for example, by Vafek in an investigation of bilayer graphene [3].

System with rotationally symmetric Fermi surface in two dimensions

We now turn our attention to the case of a two-dimensional system with a circular Fermi surface. One such system is a tight-binding lattice with the chemical potential near the minimum single-particle energy. In this case, we may approximate the dispersion as a quadratic function,

$\epsilon ({\vec {K}})={\frac {K^{2}}{2m}}.$

The associated "bare" action for this system is

$S_{0}=\int _{-\infty }^{\infty }{\frac {d\omega }{2\pi }}\int {\frac {d^{2}{\vec {K}}}{(2\pi )^{2}}}\psi ^{\ast }({\vec {K}},\omega )\left(-i\omega +{\frac {K^{2}}{2m}}-\mu \right)\psi ({\vec {K}},\omega ).$

Since we will be once again interested in modes close to the Fermi surface, we will linearize the dispersion near the surface. Letting $K_{F}={\sqrt {2m\mu }}$, we get

$\epsilon ({\vec {K}})-\mu ={\frac {K^{2}}{2m}}-\mu ={\frac {K^{2}-K_{F}^{2}}{2m}}\approx {\frac {K_{F}}{m}}(|{\vec {K}}|-K_{F}).$

If we introduce $k=|{\vec {K}}|-K_{F}$ and the Fermi velocity $v_{F}={\tfrac {K_{F}}{m}}$, we get

$\epsilon ({\vec {K}})-\mu =v_{F}k.$

Let us now switch to polar coordinates in the momentum integral, with $k$ serving as the radial coordinate. In this form, we may more easily impose the appropriate cutoff on the momentum, namely $-\Lambda <k<\Lambda$. Performing these steps, we obtain

$S_{0}=\int _{-\infty }^{\infty }{\frac {d\omega }{2\pi }}\int _{0}^{2\pi }{\frac {d\theta }{2\pi }}\int _{-\Lambda }^{\Lambda }K{\frac {dk}{2\pi }}\psi ^{\ast }(k,\theta ,\omega )(-i\omega +v_{F}k)\psi (k,\theta ,\omega ).$

We may now perform the rest of the steps required to obtain the RG transformation for this action. We may use the same transformation as we did in the one-dimensional case (we do not scale the angle $\theta$); with this choice, we may replace $K$ with $K_{F}$ since the difference proves irrelevant in the RG sense [1]. We thus take for the bare action,

$S_{0}=\int _{-\infty }^{\infty }{\frac {d\omega }{2\pi }}\int _{0}^{2\pi }{\frac {d\theta }{2\pi }}\int _{-\Lambda }^{\Lambda }{\frac {dk}{2\pi }}\psi ^{\ast }(k,\theta ,\omega )(-i\omega +v_{F}k)\psi (k,\theta ,\omega ),$

where, following Shankar, we absorb a factor of ${\sqrt {K_{F}}}$ into the fields [1]. We note that this looks almost exactly like the action for the one-dimensional case, except there is now an integral over $\theta$. Since our RG transformation is identical to the one used in the one-dimensional case, all quadratic perturbations transform in the same way as they did in that case under this transformation.

The quartic interaction will also have the same general form as before, except that now the integration measure has changed. The general form of the perturbation is now, with the momentum cutoff already imposed,

$\delta S_{4}={\frac {1}{2!2!}}\int _{K\theta \omega }u(4,3,2,1)\psi ^{\ast }(4)\psi ^{\ast }(3)\psi (2)\psi (1),$

where now

$\int _{K\theta \omega }=\prod _{i=1}^{4}\left(\int _{-\infty }^{\infty }{\frac {d\omega _{i}}{2\pi }}\int _{0}^{2\pi }{\frac {d\theta _{i}}{2\pi }}\int _{-\Lambda }^{\Lambda }{\frac {dk_{i}}{2\pi }}\right)(2\pi )^{2}\delta ({\vec {K}}_{4}+{\vec {K}}_{3}-{\vec {K}}_{2}-{\vec {K}}_{1})\times 2\pi \delta (\omega _{4}+\omega _{3}-\omega _{2}-\omega _{1}).$

For our purposes, however, we will find it convenient to eliminate the delta functions and write

$\int _{K\theta \omega }=\prod _{i=1}^{3}\left(\int _{-\infty }^{\infty }{\frac {d\omega _{i}}{2\pi }}\int _{0}^{2\pi }{\frac {d\theta _{i}}{2\pi }}\int _{-\Lambda }^{\Lambda }{\frac {dk_{i}}{2\pi }}\right)\theta (\Lambda -|k_{4}|),$

where

$k_{4}=|{\vec {K}}_{4}|-K_{F}=|{\vec {K}}_{3}-{\vec {K}}_{2}-{\vec {K}}_{1}|-K_{F}.$

The role of the theta function is to keep ${\vec {K}}_{4}$ within the cutoff we imposed. This will, unfortunately, present us with a problem when we attempt to perform our RG transformation on this interaction at tree level. To see this, let us first define

${\vec {K}}_{i}=(k_{i}+K_{F}){\vec {\Omega }}_{i}$,

where ${\vec {\Omega }}_{i}$ is a unit vector pointing along ${\vec {K}}_{i}.$ Our expression for $k_{4}$ becomes

$k_{4}=|{\vec {K}}_{4}|-K_{F}=|(k_{3}+K_{F}){\vec {\Omega }}_{3}-(k_{2}+K_{F}){\vec {\Omega }}_{2}-(k_{1}+K_{F}){\vec {\Omega }}_{1}|-K_{F}.$

In the tree-level term, we effectively replace $\Lambda$ with ${\tfrac {\Lambda }{s}}.$ This means that the theta function factor becomes

$\theta \left({\frac {\Lambda }{s}}-{\frac {|k'_{4}|}{s}}\right)=\theta \left(\Lambda -|k'_{4}|\right),$

where

$k'_{4}=s[|{\vec {K}}_{4}|-K_{F}]=s\left|\left({\frac {k'_{3}}{s}}+K_{F}\right){\vec {\Omega }}_{3}-\left({\frac {k'_{2}}{s}}+K_{F}\right){\vec {\Omega }}_{2}-\left({\frac {k'_{1}}{s}}+K_{F}\right){\vec {\Omega }}_{1}\right|-K_{F}$

$=[|(k'_{3}+sK_{F}){\vec {\Omega }}_{3}-(k'_{2}+sK_{F}){\vec {\Omega }}_{2}-(k'_{1}+sK_{F}){\vec {\Omega }}_{1}|-sK_{F}].$

We find that the theta function does not return to its original form after rescaling; we have effectively replaced $K_{F}$ with $sK_{F}$. Therefore, we cannot compare this theory to the original.

There is, however, a "trick" we can use. Since both approach the same limit as we take the limit, $\Lambda \rightarrow 0$, we will replace the theta function with an exponential:

$\theta (\Lambda -|k_{4}|)\rightarrow e^{-|k_{4}|/\Lambda }$

In this way, we have replaced a hard cutoff at $k_{4}=\pm \Lambda$ with a soft cutoff, in which values of $k_{4}$ outside the cutoff are exponentially suppressed.

References

[1] R. Shankar, Rev. Mod. Phys. 66, 129 (1994).

[2] C. N. Yang and C. P. Yang, Phys. Rev. 150, 321 (1976).

[3] O. Vafek, Phys. Rev. B 82, 205106 (2010).