Midterm 2 Solutions

Problem 1

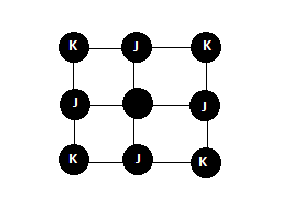
Consider a magnetic system described by an Ising model $(S_{i}=\pm 1)$ on a square lattice with $\ H=\sum _{\langle ij\rangle }J_{ij}s_{i}s_{j}+\sum _{\langle ij\rangle }K_{ij}s_{i}s_{j}$. Here, the ferromagnetic interaction $\ J_{ij}<0$ couples only nearest-neighbor spins. In contrast,the antiferromagnetic interaction $\ K_{ij}>0$ couples only the the second neighbors, i.e. spins that are "across the square" ( diagonally placed relative to each other).

a)

Image of square lattice with ferromagnetic $J_{i,j}<0$ coupling nearest neighbor spins. 
Anti-ferromagnetic $K_{i,j}<0$ coupling only second nearest neighbors. 
$Z_{FM}=4$
$Z_{AFM}=4$

b)

Problem 2

a)

b) Since Coulomb interactions are long range by $e^{2}/r$ high densities cause the formation of solids such as crystals.

f) where $T\rightarrow \infty$