Notes 2

Nuclear Astrophysics

Nuclear Astrophysics is a combination of nuclear physics and astrophysics. Nuclear physics is the study of atomic nuclei, their composition and their interactions, while astrophysics aims at studying galactic objects such as stars and galaxies. Nuclear astrophysics delves into the questions of where and when the elements were created and how nuclear reactions drive cosmic events.

The Nucleus and the forces that govern it (and some that don't)

Atomic nuclei sizes are on the scale of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 10^{-14} } meters and form the (relatively) small centers of atoms while carrying most of the mass. The basic constituents of atomic nuclei are protons (Z) and neutrons (N). Protons and neutrons are fermions (particles with half-integral spin, obey Fermi-Dirac statistics, obey the pauli exclusion princile) comprised of three quarks each, fundamental particles on a size scale of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 10^{-19} m } . The proton consist of 2 up quarks and one down quark, the neutron consist of two down quarks and one up quark. The up and down quarks have charges +2/3e and -1/3e respectively. The charges of the proton and nuetron (+1, 0) are just the sums of their constituent quarks charges. The relevant interactions on this size/mass scale are the electro-weak and strong forces.

Elements are arranged in the periodic table by order of the atomic number (Z, the number of protons in the nucleus). The atomic mass of an element is A, where A=Z+N. The radius of the nucleus is proportional to the cube root of the mass number

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle R=R_{0}A^{\frac{1}{3}}}

The strong force (SF) (also known as the Nutclear force) is a short range force that dies off after a few femto-meters (3 x 10^-15 m) (in other words, the strong force is only relevant in the nucleus of an atom) and acts on color and charge. It is 100 times stonger than EM but many many orders of magintude stronger than the other 2 forces, gravity and the weak force. The SF mediates interaction between quarks, gluons, and anti-quarks. The gluons are the exchange particles, gluons being spin 1 particles existing only inside hadrons. Hadrons feel the strong force indirectly (or they feel the residual effect of the SF). Hadrons are baryons (made of three quarks, i.e. the proton and neutron) and mesons (a quark and anti-quark pair). The strong force binds nucleons (protons and neutrons) together in the nucleus. It is charge independent, but dependent on spin orientation. Basically, the strong force glues (via gluons) protons and neutrons together.+

The range of the strong force determined by the uncertainty principle is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle R=\frac{\hbar}{mc} } where m is the mass of the virtual pion.

The weak force acts on flavor. Quarks and leptons experience this force. The W+, W-, and Z0 bosons are the mediating particles. They are all very massive which means their range is very small, as are their lifetimes. Like the strong force, the stregnth dies off rapidly with distance. The weak force in a nutshell is the force which governs nuclear decay.

The electromagnetic force acts on charged particles with the exchange particle being the photon. The Gravitational force works on all mass and energy and is mediated by the graviton.

For every matter particle there is an antimatter particle, denoted with the same symbol but with a bar over it. Antiparticles have the same mass, but have opposite values for electric charge, baryon number, and strangeness.

Definitions for Abundance

The particle abundance of isotope Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i } is defined as

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X_{i} = \frac{n_i}{\sum_j n_j} \, }

where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n_i } is the the number density of particle Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i } , and the sum is taken over all isotopes present. It is also useful to define a relative particle abundance, which is set logarithmically and normalized to the abundance of hydrogen:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon_i = \log_{10} X_i + 12 \ . }

The mass fraction is the fraction of total mass in the sample constituted by species Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i } :

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X_i = \frac{m_i}{m_{tot}} = \frac{m_i n_i}{\rho} \approx \frac{A_i n_i}{\rho N_A} } ( Note that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m_i \approx A_i m_u \ } and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m_u = \frac{m_{12C}}{12} = \frac{1}{N_A} } )

Denoting Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Y_i\,} the mass per baryon, as

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Y_i \equiv \frac{X_i}{A_i} , }

allows us to define the particle's number density by the density of the sample and this baryon fraction,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n_i = Y_i \rho N_A \ . }

Another useful quantity is the average mass number, or mean molecular weight, defined by

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu_i = \frac{\sum_i{A_i Y_i}}{\sum_i{Y_i}} = \frac{\sum_i{X_i}}{\sum_iY_i} = \frac{1}{\sum_i{Y_i}}}

The electron abundance

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Y_e = \sum_i Z_i Y_i \ } , which can also be normalized to 1 as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Y_e = \frac{\sum_i{Z_i Y_i}}{\sum_i{A_i Y_i}} ,}

is the ratio of protons to nucleons in the sample, and similarly to nuclei, the electron number density is found by

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n_e = Y_e \rho N_A \ . }

Determining Solar Abundances

It is widely held that the solar system was formed partly from the gravitational collapse of interstellar matter billions of years ago. If so, then a study of the elemental abundances in our solar system should give us a window to what comprised our region of the galaxy at that time. There are several methods of determining the elemental abundances in our solar system.

Terrestrial methods

Examining the materials that we find on earth can yield the desired abundances. However when studying “native” rocks one must be careful in interpreting the data. Through time chemical fractionation would have separated out some of the elements and affected their distribution. However, chemical processes are not dependent on which isotope of the element is involved. Therefore on Earth the distribution of the isotopes within each element should be the same as when the solar system came into existence.

An exception to the chemical fractionation problem is found in the study of a certain class of meteorites called carbonaceous chondrites. About 6% of all meteorites fall into this category. What is significant here is that they appear to have experienced very little heating; therefore they have undergone minimal chemical process and should reflect what the accurate solar system abundances are.

Extra Terrestrial methods

By observing electromagnetic radiation from the sun we may also determine elemental distributions. This follows the basic premise that each element and chemical compound has its own energy levels and therefore its own unique pattern of absorption and emission lines. One must simply examine the received solar spectra and resolve these patterns to detect these elements and compounds. A complication of this method is that one must have a precise statistical knowledge of how the atoms are ionized and how they interact with photons and other particles like atoms and electrons.

Properties of Astrophysical Plasmas

Quantum Mechanics

A knowledge of quantum mechanics is necessary for many astrophysical calculations. This is Schrödinger's equation:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{H}\left |\Psi\right \rangle = i\hbar\frac{\partial }{\partial t}\left |\Psi\right \rangle}

where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{H}} is the Hamiltonian operator and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left |\Psi\right \rangle} is the complex state vector describing the quantum mechanical state of the system. In this notation the right-pointing vector is called the ket while left pointing vectors are called bra. The joining of a bra and a ket represents the inner product between the two which is a scalar: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left\langle \Phi | \Psi \right\rangle} . In the position representation we define the wave function Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi(\vec{x},t) = \left \langle x | \Psi \right \rangle} The probability density of this system is given by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\psi|^2 = \psi*\psi} which must be normalized when integrated over all (relevant) space:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left \langle \Psi|\Psi \right \rangle = \int_{}^{} |\psi|^2 d^3x = 1}

In the presence of conservative forces the Hamiltonian operator can be expressed in a the classically equivalent form (for one particle):

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{H} = \frac{\hat{p}^2}{2m} + \hat{V} = -\frac{\hbar^2}{2m}\nabla^2 + V(\vec{x},t)}

where the position representation of the momentum operator is used: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{p} = \frac{\hbar}{i}\vec{\nabla}}

A notable case for us is that where the potential is time-independent: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V = V(\vec{x})} . In such a case the separation of variables method can be applied and the time-dependent part of Schrödinger's equation can be separated from the space-dependent part. This will yield the time-independent Schrödinger's equation (TISE):

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{-\hbar^2}{2m}\nabla^2\phi(\vec{x}) + V(\vec{x})\phi(\vec{x}) = E\phi(\vec{x})}

where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi} is the position dependent part (stationary state) of the wave function and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E} is defined as the energy of the state.

For a collection of n particles we may write the TISE as:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(\sum_{i=1}^{n}\frac{-\hbar^2}{2m_i}\nabla_i^2\right)\phi_{1,2,...,n} + \left (\sum_{i=1}^{n}\sum_{j=i}^{n}V_{ij}\right )\phi_{1,2,...,n} = E\phi_{1,2,...,n}}

where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \nabla_i^2} is the Laplacian operator acting on Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{x}_i} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_{ij}} is the potential energy between particles i and j. For a non-interacting system Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_{ij} = 0} for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i \neq j} and we may use separation of variables again to express the stationary state as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi_{1,2,...,n} = \phi_1\phi_2...\phi_n } and the TISE for the entire system as a set of independent TISE's for each particle.

The TISE for a system of free (Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V = 0} ), non-interacting particles in a Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle d\times d\times d} volume yields single particle eigenenergies of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E = \frac{\pi^2 \hbar^2}{2md^2}(n_x^2 + n_y^2 + n_z^2)}

where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n_x} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n_y} , and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n_z} can each be any integer greater than zero.

Fermi Gases

Every quantum particle in nature can either be classified as a fermion or a boson. Identical fermions are known to always have wave functions that are anti-symmetric, i.e. Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi_{1,2} = -\psi_{2,1}} while identical bosons are known to have wave functions that are symmetric, i.e. Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi_{1,2} = \psi_{2,1}} . This knowledge is necessary to formulate a thermodynamic theory for gases composed of these kinds of particles.

For Fermions some detailed calculation in statistical mechanics yields that their occupation distribution is

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(E) = \frac{1}{e^{(E-\mu)/kT} + 1} }

Using the non-relativistic density of states expression Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega(E) = \frac{2\pi g}{h^3}(2m)^{3/2}E^{1/2}} we can find the (non-relativistic) particle density:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n = \int_{0}^{\infty} \omega (E) f(E) dE = \int_{0}^{\infty} \frac{2\pi g}{h^3}(2m)^{3/2}E^{1/2} \frac{1}{e^{(E-\mu)/kT} + 1} dE = \frac{4\pi (2m)^{3/2}}{h^3}\int_{0}^{\infty}\frac{E^{1/2}}{e^{(E-\mu)/kT} + 1}dE}

where we substituted g = 2 which is the spin degeneracy factor for spin-1/2 fermions. Now we make a coordinate transformation Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x = \frac{E}{kT}} . This gives

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n = 4\pi \frac{(2mkT)^{3/2}}{h^3}F_{1/2}\left (\frac{-\mu}{kT}\right )}

where the Fermi function Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F_{n}(z) = \int_{0}^{\infty}\frac{x^n}{1+e^{x+z}}dx}

Similarly for the pressure,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P = \frac{1}{3}\int_{0}^{\infty}pv\omega (E) f(E) dE = \frac{4\pi (2m)^{3/2}}{3h^3}\int_{0}^{\infty}\frac{2E^{3/2}}{e^{(E-\mu)/kT}+1}dE}

where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p = mv} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E = p^2/2m} . Finally we may write

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P = \frac{8\pi (2m)^{3/2} (kT)^{5/2}}{3h^3}F_{3/2}\left ( -\frac{\mu}{kT} \right )}

3rd subtopic (Brett)

work in progresss...

For Bosons some detailed calculation in statistical mechanics yields that their occupation distribution is

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(E) = \frac{1}{e^{(E-\mu)/kT} - 1} }

Using the non-relativistic density of states expression Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega(E) = \frac{2\pi g}{h^3}(2m)^{3/2}E^{1/2}} we can find the (non-relativistic) particle density:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n = \int_{0}^{\infty} \omega (E) f(E) dE = \int_{0}^{\infty} \frac{2\pi g}{h^3}(2m)^{3/2}E^{1/2} \frac{1}{e^{(E-\mu)/kT} - 1} dE = \frac{4\pi (2m)^{3/2}}{h^3}\int_{0}^{\infty}\frac{E^{1/2}}{e^{(E-\mu)/kT} - 1}dE}

where we substituted g = 2 which is the spin degeneracy factor for spin-1/2 Bosons.

Any number of bosons can occupy the same sublevel.

Now we make a coordinate transformation Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x = \frac{E}{kT}} . This gives

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n = 4\pi \frac{(2mkT)^{3/2}}{h^3}F_{1/2}\left (\frac{-\mu}{kT}\right )}

where the Fermi function Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F_{n}(z) = \int_{0}^{\infty}\frac{x^n}{1+e^{x+z}}dx}

Similarly for the pressure,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P = \frac{1}{3}\int_{0}^{\infty}pv\omega (E) f(E) dE = \frac{4\pi (2m)^{3/2}}{3h^3}\int_{0}^{\infty}\frac{2E^{3/2}}{e^{(E-\mu)/kT}-1}dE}

where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p = mv} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E = p^2/2m} . Finally we may write

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P = \frac{8\pi (2m)^{3/2} (kT)^{5/2}}{3h^3}F_{3/2}\left ( -\frac{\mu}{kT} \right )}

Astrophysical Application

To maintain hydrostatic equilibrium, internal gas pressure in stellar structure must be balanced by the gravitational force acting. Estimates for stellar structure can be calculated from

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial P_r}{\partial r} = - \rho_r \frac{Gm_r}{r^2} }

as well as the equation of mass conservation,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial M_r}{\partial r} = 4\pi r^2\rho_r \ . }

Note that for a non-relativistic degenerate gas, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P \ } is proportional to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho^{5/3} \ } , while it is proportional to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho^{4/3} \ } in the case of a relativistic degenerate gas.

We can begin to make corrections in these estimates of stellar structure by adding a term of internal energy to account for interactions, (as we were treating the stellar matter as an ideal gas above), i.e.

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P = \sum_i {P_i} + \sum_j \left ({\frac{\partial U_{int,j}}{\partial V}}\right )_{S,N_i} }

An example of an area of research under this application is calculating the equation of state at extreme densities, and determinations of how the equation of state has an influence on the mass and radius of a neutron star.

Basic Nuclear Physics and Decays

Nuclear Models

Independent Particle Model

In the independent particle model of the nucleus the protons and neutrons are assumed to be a non-interacting cold Fermi gas in a confined volume. In this case integration of the density of states up to the Fermi energy will yield the total particle density:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n = \int_{0}^{E_F}\omega(E)dE \propto \int_{0}^{E_F}E^{1/2}dE} according to the non-relativistic density of states expression. Solving for the Fermi energy yields:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_F = \frac{h^2}{2m}\left ( \frac{3n}{8\pi} \right )^{2/3} } .

The mean energy per nucleon is given by

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \overline{E}=\frac{1}{n}\int_{0}^{E_F}E\omega(E)dE} which yields Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \overline{E}=\frac{3}{5}E_F}

This results in about 8-12 MeV of energy per nucleon.

Droplet Model

In the droplet model the nucleons are assumed to interact strongly within the nucleus like in a liquid droplet. Under dense packing the nucleons in the interior are surrounded by 12 other nucleons and is sharing binding energy with each. At the surface the nucleons share binding energy with fewer other nucleons which results in a negative correction. The Coulomb repulsion of the protons within the nucleus also results in a negative correction as well. Asymmetry of the number of protons versus the number of neutrons also results in a negative energy correction due to the Pauli exclusion principle. The tendency of protons and neutrons to form Cooper pairs also gives an energy correction. The sum of all the contributions are:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B(Z,A) = a_{Vol} A - a_{Surf} A^{2/3} - a_{Coul} A \frac{Z^2}{A^{1/3}} - a_{Sym} \frac{(Z-\frac{A}{2})^2}{A} + (+/-/0) \frac{12}{A^{1/2}}}

where for the last term which takes into account the Cooper pair energy correction the plus sign is for Z and A - Z both even, the minus sign is for Z and A - Z both odd and the zero is for A being odd.

The constants can be given as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_{Vol} = 16MeV} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_{Surf} = 18.5MeV} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_{Coul} = 0.72MeV} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_{Sym} = 23.4MeV} .

Weak Decay

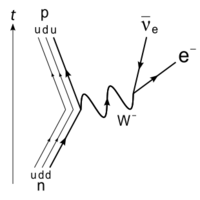
Decays via the weak interaction have much longer time scales than those of the electromagnetic and strong interactions, because they are mediated by massive bosons with very short life times (~ Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 10^{-25} } s). Due to this, the force is short in range and and 'weak', causing weak decays to be less likely to occur. For a simple example, we can consider the beta decay of a free neutron, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n \rightarrow p + e^- + \bar v_e } , which has a mean lifetime of just under 15 minutes - obviously much longer than strong/electromagnetic timescales. Another particle that undergoes weak decay is the charged pion, which has a life time of ~Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 10^{-8} } s, still many orders of magnitude longer than timescales for strong or electromagnetic interaction. Note that in weak decay Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A } (the number of nucleons) does not change.

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta^- } Decay (also known as electron emission) is a type of weak decay in which a neutron in the nucleus is converted to a proton, and an electron and electron anti-neutrino are emitted. This type of decay usually occurs in neutron rich nuclei (below the line of stability), and is given by

$(Z,A)\rightarrow (Z+1,A)+e^{-}+{\bar {v}}_{e}\$

$M_{nuc}(Z,A)>M_{nuc}(Z+1,A)+m_{e}\$

$M_{at}(Z,A)>M_{at}(Z+1,A)\$

$\beta ^{+}$ Decay (also known as positron emission) is a type a weak decay where a proton is converted to a neutron, and a positron and electron neutrino are emitted, given by

$(Z,A)\rightarrow (Z-1,A)+e^{+}+v_{e}\$

$M_{nuc}(Z,A)>M_{nuc}(Z-1,A)+m_{e}\$

$M_{at}(Z,A)>M_{at}(Z-1,A)+2m_{e}\$

Note that unlike $\beta ^{-}$ decay, this reaction can not occur in isolation, as the mass of a neutron is greater than that of a proton. Also, the $2m_{e}$ term in the last condition comes from the annihilation energy of the emitted positron with a nearby electron in the environment, and this type of decay can only occur when the difference in atomic masses is greater than this energy.

Electron capture is a slightly different kind of decay, in which a nucleus gains an electron, emitting a neutron and an electron neutrino. This type of decay has a Q value which is $2m_{e}$ lower than $\beta ^{+}$ decay, and therefore usually occurs in proton rich nuclei, typically in regions of very high density or temperature. Electron capture is given by

$(Z,A)+e^{-}\rightarrow (Z-1,A)+v_{e}\$

$M_{nuc}(Z,A)+m_{e}>M_{nuc}(Z-1,A)\$

$M_{at}(Z,A)>M_{at}(Z-1,A)\$

In electron capture, the atom will also emit an X-ray as the captured electron's hole in the atomic shell is filled.

Due to the fact that $\beta$-decays don't have to overcome the Coulomb Barrier, they will always occur (when possible). Also, note that for a nuclei with odd $A$, there is only one stable nuclei along the isobaric chain (the chain the nuclei decays along in the table of nuclides), while there are 2 stable states for nuclei with even $A$.

Nuclear Reactions and Cross Sections

In general, we can write a nuclear reaction as $A(i,j)B,\$ where $i\$ is the light incoming projectile, $A\$ is the target nucleus, and $j\$ & $B\$ are the lighter particle and heavy nucleus that result from the reaction.

We can generally think of there being 2 types of reactions, direct reactions and resonant reactions. A direct reaction occurs when the interacting nuclei make a direct transition into a bound state, for example, neutron capture. On the other hand, when a resonant reaction occurs, the interacting particles form an unstable compound nucleus, which then decays to a stable state. For resonant reactions, the probability for an interaction to occur (ie. the differential cross section) is enhanced when the energy of the incident particle corresponds to an energy level in the target nuclei.

Transmission Coefficients

For a nucleus to undergo a decay, the decaying particle must tunnel through the barrier created by the coulomb potential of the nucleus. It is necessary for the discussion of nuclear reactions to find the probability for this to occur for a given system.

Defining the Quantum Mechanical Flux as

${\overrightarrow {j}}={\frac {\hbar }{2m_{i}}}\left(\phi ^{*}{\overrightarrow {\nabla }}\phi -\phi {\overrightarrow {\nabla }}\phi ^{*}\right)$

allows us to calculate the Transition Probability, which is the probability for a particle to tunnel through a coulomb barrier, as the ratio of final flux to the initial flux, ie

$T={\frac {j_{fin}}{j_{in}}}={\frac {k_{fin}|\phi _{fin}|^{2}}{k_{in}|\phi _{in}|^{2}}}$.

Transition Probabilities for Several Potentials

Given a Box Potential, for example neutron emission, where the neutron feels no coulomb barrier, we find

$T\approx {\frac {4k_{1}}{k_{2}}}$.

Adding a Square Potential to the above defined box potential, the tunneling probability is found to be

$T\propto e^{-{\frac {2}{\hbar }}{\sqrt {2m(E-V)}}d}$

For a box potential with some additional general potential $V(x),\$ the transition can be found using the WKB approximation,

$T\approx e^{-{\frac {2}{\hbar }}\int _{x_{1}}^{x_{2}}{\sqrt {2m(V(x)-E))}}dx}.$

If the potential $V(x)\$ is know to be a coulomb potential $\left(V_{c}={\frac {Z_{1}Z_{2}e^{2}}{x}}\right)\$, the tunneling probability is defined as $T=e^{-2\pi \eta }\$ where

$\eta ={\sqrt {\frac {m}{2E}}}{\frac {Z_{1}Z_{2}e^{2}}{\hbar }}$

is known as the Sommerfeld parameter.

Resonance Reactions

Resonance phenomena are a complication in measuring nuclear cross sections. The cross section between two colliding nuclei will be greater when their energy is at or near one of the excitation energies of the compound nucleus. A simple example of this kind of phenomenon is seen in solving the TISE in 3-D for a neutron scattering off of a square-barrier potential. The following is a plot of the inner amplitude squared divided by the outer amplitude squared versus V, the depth of the well in the interior region.

The energy of the neutron was 5 MeV with the barrier being 3 fm from the center and 5 fm wide. The peaks are resonance peaks and arise from the particular wave function conditions at the boundaries.

Statistical model (Hauber-Feshbach)

$\sigma _{i}(j,o)={\frac {\pi }{k_{j}^{2}}}{\frac {1+\delta _{i,j}}{(2I_{i}+1)(2I_{j}+1)}}\sum _{J,\pi }(2J+1){\frac {T_{j}(E,J,\pi )T_{o}(E,J,\pi )}{T_{tot}(E,J,\pi )}}$

Thermonuclear Reactions

Determining the reaction rates

The averaged probability of reaction between two particles per second times volume is given by:

$\left\langle \sigma \upsilon \right\rangle =\left({\frac {8}{\mu \pi }}\right)^{1/2}{\frac {1}{(kT)^{3/2}}}\int _{0}^{\infty }E\sigma e^{\frac {-E}{kT}}dE$

The Main Sequence: Hydrogen Burning

Neutrino theory

Neutrino physics is very important in understanding nuclear reactions in stars. In the sun, about 3 percent of the energy generated is in the form of neutrinos. They escape at near the speed of light and travel everywhere through everything, due to their extremely small cross sections with normal matter. Indeed we have tens of billions of solar neutrinos passing through every square centimeter facing the sun, per second. Also, since gamma radiation from the nuclear reactions are never directly seen the sun's core, the neutrinos themselves are direct evidence that thermonuclear reactions are indeed taking place inside of the sun.

There are three generations of neutrinos: the electron neutrino ($\nu _{e}$), the muon neutrino ($\nu _{\mu }$), the tau neutrino ($\nu _{\tau }$) and their corresponding anti-particles. The masses of the neutrinos themselves are not known but their mass differences can be measured. The energies inside of the sun are not sufficient to generate any kind except electron neutrinos as seen in the figure.

Now the flavor states of the neutrinos (electron, muon, tau) which enter into the standard model Lagrangian and govern the interactions are known to be different from the mass states which govern the propagation of the particles through space. The mass states are mixtures of the flavor states and the flavor states are mixtures of the mass states. The mass states each propagate with a different phase velocity and the interference between the phases changes the proportion of the masses that would be measured at that point in space. This results in the neutrino oscillation phenomena, meaning that some electron neutrinos leaving the sun will be measured on earth as muon or tau neutrinos. This observation led to the solving of the "solar neutrino problem" where about 1/3 to 2/3 of the measured solar neutrinos were found to missing in earth-bound detectors.

For two species of neutrinos, say the electron and the muon, the mixing between the mass states $\nu _{1}{\frac {}{}}$ and $\nu _{2}{\frac {}{}}$ can be given by a mixing angle:

$\nu _{e}=\nu _{1}\cos {\theta }+\nu _{2}\sin {\theta }{\frac {}{}}$ and $\nu _{\mu }=-\nu _{1}\sin {\theta }+\nu _{2}\cos {\theta }{\frac {}{}}$

and inverting the equations for the mass states gives:

$\nu _{1}=\nu _{e}\cos {\theta }-\nu _{\mu }\sin {\theta }{\frac {}{}}$ and $\nu _{2}=\nu _{e}\sin {\theta }+\nu _{\mu }\cos {\theta }{\frac {}{}}$

In the vacuum, the single particle solutions to the Schroedinger equation for each mass eigenstate are: $\psi _{1/2}(t)=\psi (0)e^{-iE_{1/2}t}{\frac {}{}}$

where $E_{1}{\frac {}{}}$ and $E_{2}{\frac {}{}}$ are the energies of those two mass states.

Choosing a

.

Post-Main-Sequence Evolution: He Burning

The Triple Alpha Process and Carbon burning rate

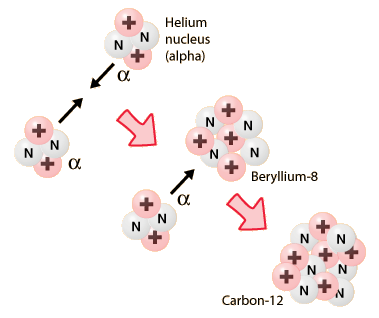
When much of the hydrogen in a star's core has been consumed and the conditions are favorable to burn Helium-4, the only possible way to burn it is by further alpha capture and not by proton capture. The reason for this is that proton capture yields Lithium 5 which is highly unstable and decays back to Helium-4 in about $10^{-22}$ seconds. Helium-4 fused with Helium-4 gives Beryllium-8 which decays within $10^{-17}$ seconds but may absorb a third alpha within that time period and yield stable Carbon-12:

$^{4}He(\alpha ,-)^{8}Be(\alpha ,-)^{12}C^{+}{\frac {}{}}$

This is possible once core temperatures exceed 100 million Kelvin because a significant amount of Beryllium-8 needs to be maintained in the core by alpha-alpha fusion.

The excitation energy of the Carbon-12 nucleus generated would be about 7.7 MeV. In 1954 Fred Hoyle predicted that there must be a natural excitation of Carbon-12 around this energy in order to make this a resonant reaction. The reason he did this was because the amount of Carbon-12 a direct capture model yielded was not enough to produce the amount of Carbon-12 seen in the universe. Three years later Fowler et al. discovered Hoyle's resonance of Carbon right at 7.65 MeV.

Using the equilibrium condition between the excited Carbon-12 and Helium-4, one finds that the relation between the abundances is:

$Y_{^{12}C(7.6MeV)}=3^{3/2}Y_{^{4}He}^{3}\rho ^{2}N_{A}^{2}\left({\frac {2\pi \hbar ^{2}}{m_{^{4}He}kT}}\right)^{3}exp^{-Q/kT}$

where $Q=(m_{^{12}C(7.6MeV)}-3m_{^{4}He})c^{2}$

The reaction rate is $3^{3/2}\rho ^{2}N_{A}^{2}Y_{^{4}He}\left({\frac {2\pi \hbar ^{2}}{m_{^{4}He}kT}}\right)^{3}{\frac {\Gamma _{\gamma }}{\hbar }}exp^{-Q/kT}$.

There is no such lucky resonance for the alpha capture of carbon to form Oxygen-16 but it can be created via sub-threshold or high lying resonances. This is enough to generate some oxygen from the carbon and helium abundances. However due to parity conditions in the excitation levels of Neon 20, alpha capture of Oxygen-16 is not allowed.

The alpha-Carbon cross section is the most important nuclear physics uncertainty in astrophysics. This is because the relevant energies in stars are so low that experiments must produce a very high flux of particles in order to get sufficient data points and hence the error bars in the data are large. If we could know it precisely then the C/O ratio in the core could be better ascertained and that would affect later nucleosynthesis.

The major reactions during Helium burning are

for energy generation: $^{4}He(2\alpha ,\gamma )^{12}C{\frac {}{}}$ and $^{12}C(\alpha ,\gamma )^{16}O{\frac {}{}}$ and for neutron generation: $^{14}N(\alpha ,\gamma )^{18}F(e^{+},\nu _{e})^{18}O(\alpha ,\gamma )^{22}Ne(\alpha ,n)^{25}Mg{\frac {}{}}$ and $^{12}C(p,\gamma )^{13}N(e^{+},\nu _{e})^{13}C(\alpha ,n)^{16}O{\frac {}{}}$.

Post Main-Sequence Evolution: Beyond He Burning

Carbon Burning

When the helium in the center of a star has been consumed, the core will begin to contract, causing temperature and density to rise until sufficient conditions for igniting the next stage of energy generation have been reached. At the conclusion of He burning, the core is dominated by $^{12}{\textrm {C}}$ and $^{16}{\textrm {O}}$ , so as seems logical the next stage of burning is $^{12}{\textrm {C}}+^{12}{\textrm {C}}$, because this process feels the lowest Coulomb barrier of the possible reactions between these nuclei. Due to the extreme conditions necessary to overcome this barrier, only stars of over 8 solar masses at ZAMS will reach this burning stage. To initiate carbon burning, we must have temperatures of ~ 600 to 700 million K and densities over ~ $3*10^{6}g/cm^{3}$. The primary reactions involved in this stage of burning are as follows:

$^{12}{\textrm {C}}(^{12}{\textrm {C}},-)^{24}{\textrm {Mg}}^{*}\$

Where the $^{24}{\textrm {Mg}}^{*}$ nucleus formed is highly excited (this reaction has a very high Q-value of about 14 MeV), and the excess energy is most efficiently released by immediately emitting a light massive particle (p,n,$\alpha$) through one of the following decays, rather than through a photon.

$\rightarrow ^{23}{\textrm {Mg}}+n-2.62MeV$

$\rightarrow ^{20}{\textrm {Ne}}+\alpha +4.62MeV$

$\rightarrow ^{23}{\textrm {Na}}+p+2.24MeV$

We can easily tell the reaction which forms $^{20}{\textrm {Ne}}$ will dominate because it is much more favorable energetically, and that the first reaction is endothermic and can only occur above the given threshold energy level. The light particles released by these processes will go on to initiate a chain of secondary reactions, involving the products of the above primary reactions and the ashes of helium burning. At the conclusion of carbon burning, the core will be composed mostly of $^{16}{\textrm {O}},^{20}{\textrm {Ne}},^{23}{\textrm {Na}},$ and $^{24}{\textrm {Mg}}$.

Neon Burning

Once again, when the carbon in the core is consumed and this stage of burning has concluded, the core will contract, causing temperature and density to rise until the next burning stage is reached. It seems logical that the next process would involve the fusion of oxygen nuclei, as these are the lightest species left in the core in high abundance, and therefore they experienced the lowest barrier. However, before the conditions necessary for this reaction are met, the core will reach high enough temperatures for the photodisintegration of Neon to occur. Photodisintegration is a process in which a highly energized photon interacts with a nuclei, sending it into an excited state, where the nuclei immediately decays by emitting a proton, neutron, or alpha particle. To initiate this stage of burning, we need temperatures of ~ 1.3-1.7 billion K, a condition that will only be reached by stars of at least 12 solar masses at ZAMS.

In this stage of burning, initially an equilibrium is established between the forward and backward reactions $^{20}{\textrm {Ne}}(\gamma ,\alpha )^{16}{\textrm {O}}\$ and $^{16}{\textrm {O}}(\alpha ,\gamma )^{20}{\textrm {Ne}}\$, which is then followed by $^{20}{\textrm {Ne}}(\alpha ,\gamma )^{24}{\textrm {Mg}}\$ (using the products of each of the previous reactions), giving the net effect of

$2^{20}{\textrm {Ne}}\rightarrow ^{16}{\textrm {O}}+^{24}{\textrm {Mg}}+4.59MeV$

A few important secondary reactions making up this network are:

$^{23}{\textrm {Na}}(p,\alpha )^{2}0{\textrm {Ne}}\$

$^{20}{\textrm {Ne}}(\alpha ,\gamma )^{24}{\textrm {Mg}}(\alpha ,\gamma )^{28}{\textrm {Si}}\$

$^{23}{\textrm {Na}}(\alpha ,p)^{26}{\textrm {Mg}}(\alpha ,n)^{29}{\textrm {Si}}\$

$^{20}{\textrm {Ne}}(n,\gamma )^{21}{\textrm {Ne}}(\alpha ,n)^{24}{\textrm {Mg}}(n,\gamma )^{25}{\textrm {mg}}(\alpha ,n)^{28}{\textrm {Si}}\$

Inverse Reaction Rates

To determine the reaction rate for a process such as $^{20}{\textrm {Ne}}(\gamma ,\alpha )^{16}{\textrm {O}}\$ in the above network, it is necessary to use a relationship between this reaction rate and that of the inverse reaction ( $^{16}{\textrm {O}}(\alpha ,\gamma )^{20}{\textrm {Ne}}\$), along with the principle of detailed balance. Considering an arbitrary reaction $A+B\rightarrow C$, we can use the Saha equation to determine abundance ratios:

${\frac {n_{A}n_{B}}{n_{C}}}={\frac {g_{A}g_{B}}{g_{C}}}\left({\frac {m_{A}m_{B}}{m_{C}}}\right)^{3/2}\left({\frac {kT}{2\pi h^{2}}}\right)^{3/2}e^{-Q/kT}\$

We also know that abundances are constant when in NSE, therefore

${\frac {\mathrm {dn_{C}} }{\mathrm {d} t}}=n_{A}n_{B}\left\langle {\sigma v}\right\rangle -\lambda _{C}n_{C}=0\$

where $\lambda _{C}$ is the decay rate of species C, and $\left\langle \sigma v\right\rangle$ is the $A+B\rightarrow C$ reaction rate. Combining these equations, we find the ratio of reaction rates to be

${\frac {\lambda _{C}}{\left\langle \sigma v\right\rangle }}={\frac {g_{A}g_{B}}{g_{C}}}\left({\frac {m_{A}m_{B}}{m_{C}}}\right)^{3/2}\left({\frac {kT}{2\pi h^{2}}}\right)^{3/2}e^{-Q/kT}\$

Finally, we can introduce the chemical potential ($\mu \$), found through

$\mu =mc^{2}+kTln\left[{\frac {n}{g}}\left({\frac {h^{2}}{2\pi mkT}}\right)^{3/2}\right]\$

allowing us to solve for the abundance ratio, which we find to be independent of any rates, needing only the density, temperature, and the mass & partition function of each relevant nuclei to determine abundances:

$Y(Z,N)=Y_{p}^{Z}Y_{n}^{N}G(Z,N)(\rho N_{A})^{A-1}{\frac {A^{3/2}}{2^{A}}}\left({\frac {2\pi h^{2}}{m_{u}kT}}\right)^{{\frac {3}{2}}(A-1)}e^{B(Z,N)/kT}\$

Core Collapse Supernovae

Nucleosynthesis in Core Collapse Supernovae

During the core collapse phase of stellar evolution the conditions exist where the temperatures are 1-9 billion K and the densities are 10^7 to 10^10 g/cm^3. The composition of the core is mostly of iron group elements. Some important reactions take place while the core collapses. These are electron capture:

$e^{-}+(N,Z)\to (N+1,Z-1)+\nu _{e}{\frac {}{}}$

and beta decay:

$(N,Z)\to (N-1,Z+1)+e^{-}+{\bar {\nu }}_{e}$

The electron capture rates can be modeled differently with different results. The Fuller Fowler Newman Independent Particle Picture and the Shell Model exhibit the same trends but at different orders of magnitude for the Cobalt isotopes 55, 59, 60 and Manganese 54. Some variation between those two models for beta decay rates also exists for the iron group elements, especially Manganese isotopes 56 and 59, and Iron isotopes 59 and 60.

During the latter portion of the collapse we get proton electron capture:

$e^{-}+p\rightleftharpoons n+\nu _{e}$

and neutrino scattering equilibrium:

$\nu +A\rightleftharpoons \nu +A$ (trapping)

$\nu +e^{-}\rightleftharpoons \nu +e^{-}$ (thermalization)

The electron capture reduces the $Y_{e}$ which in turns reduces the degeneracy pressure further aiding the collapse. Modeling the explosion itself has issues. The major issue is that no mechanism is currently known to eject the envelope of the star without stalling and falling back in. The approach used is then to model a star in the latter stage of its evolution and manually send a shock-wave of about 10^51 ergs from the edge of the iron shell propagating outwards. The neutrino flux is guessed at near 10^53 erg. Then the propagation of the shock-wave is calculated. A mass-cut is chosen which is the division in the structure where matter stays in the core on the inside and ejected on the outside.

Nucleosynthesis is determined by a competition of the nuclear time scale and the hydrodynamic (expansion) time scale. The reactions are limited to those which can take place within the expansion time at the given density. In the explosion some important processes are explosion Oxygen and Silicon burning by alpha capture. Many alpha particles are generated from the core itself by photo-disintegration of iron by high energy gamma rays. The shock wave compresses the outer layers making heavy elements. Neutrinos irradiate the outer layers creating rare isotopes of heavy elements and knocking off nucleons in the Helium layer.

Heavy Nuclei beyond Iron I and II

slides 1 - 20

Nuclei Beyond Iron are created by either the slow or rapid neutron capture process. The s process works by neutron capture but happens at a rate slow compared to beta decay. Therefore if an element is made which beta decays in a time shorter than the neutron capture time (defined by the cross section of the particular particle and a neutron), the chain of neutron capture will cease at that element and no heavier isotope of a particular element will not be made by the s process, But rather the r process, in which case the temperature and density are both high enough for the cross section of neutron capture to be large enough to make the time for neutron capture smnall compared to the rate of beta decay for even an unstable nucleus such that the r process can diverge much further from the line of stable nuclides than can the s process.