PHZ3400-09 Emergence in Condensed Matter

“ The whole is more than the sum of its parts ” -Aristotle

Group 1 is cool too

Emergence Artist's view of Emergence Header Bold Text Normal Text Bold Text Normal Text

Emergence is the way complex systems and patterns arise out of a multiplicity of relatively simple interactions. Emergence is central to the theories of integrative levels and of complex systems.

Emergence can be defined as: "the arising of novel and coherent structures, patterns and properties during the process of self-organization in complex systems" according to Professor Jeffrey Goldstein in the School of Business at Adelphi University.

The following points concern the scope of matter that we're studying, from the smallest quantum mechanics to the largest macroscopic molecules.

Do we have to watch every atom?

Are we concerned about the macroscopic or the microscopic? This is a question of granularity.

This is a question of granularity and the answer to it depends on the context of the problem. If one is looking at the motion of a soccer ball as a whole then the answer is no. In this case, we are comprising our system of large components, mainly the soccer ball. The particles of air inside the ball move randomly, but there is no point in keeping track of every air particle in the ball, if all we care about is the overall motion of the ball. This is an example of coarse-graining, where only large particles comprise the system of interest. In condensed matter physics, scientists often begin with a microscopic system and use coarse graining to achieve a description of a macroscopic system.

However, if one wanted to know the air pressure inside the ball, knowing properties of the individual particles is probably more convenient. This is an example of fine-grained system.

When deciding on using a coarse-grained or fine-grained system, one should decide if the property desired is macroscopic or microscopic.

Macroscopic Bodies

A macroscopic body is made up of many microscopic bodies usually on the order of at least one mole. The amount of particles in one mole is given by Avogadro's number, on the order of $\mathbb {N} _{A}=10^{23}$. Were every particle to be watched, there would be something on the order of $e^{10^{23}}$ states to solve for, a significantly high number capable of being too much for even the best computers.

Center of Mass

Rather than tracking every atom, we simplify things with using only the center of mass to draw a complete picture about the object. This allows for a few degrees of freedom. The Center of Mass is found using the following expression:

$m_{CM}={\dfrac {\sum _{i}^{N}m_{i}R_{i}}{\sum _{i}^{N}m_{i}}}$

Center of mass is an example of a collective co-ordinate in which all of the particles are treated as one.

Phases of Matter

Matter is observed macroscopically as a set of collective and observable coordinates, as opposed to a collection of wiggling atoms. On Earth, matter comes in 3 phases depending on temperature: solid, liquid, and gas. There is one more phase that can only be found on the sun: plasma. But we're not concerned about that here.

Phase diagram used in a chocolate factory (do you believe it?).

Snow Flake.

Carbon Phase Diagram.

Water comes in solid (like the snowflake shown), liquid, and gaseous forms. What governs these transitions for water is temperature. To compound this phenomenon further, compounds, such as carbon chains, can have different types of the same state, which for solid carbon includes graphite, coal, and diamonds. These different forms of the same state are known as allotropes. The pressure-temperature graph to the right shows that these different types of solid carbon are formed at different pressures.

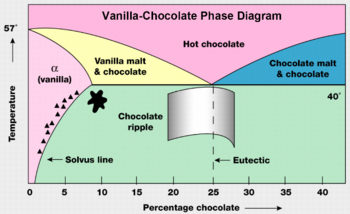
Another method of phase shifting can be seen in the vanilla-chocolate phase diagram. As one can see the percent of chocolate in the vanilla-chocolate mixture also can cause a phase shift. Though this example appears simplistic, compounds do exhibit property changes as the proportions of the constituent elements change.

Importance of Quantum Mechanics

The cause of these phase changes is an interesting question. Can these phase changes be found by classical or quantum mechanical means?

For example, why don't we suffer the fate of Rumpelstinskin (drop through the floor)? This is because objects are solid. But is solidity a quantum or classical phenomena? Solidity is most (are we sure or it's a guess??) likely a macroscopic property as solids contain many particles. But classical physics gives no reason for objects to be solid other than molecular vibrations from the temperature of the solid. So ideally one could manipulate the temperature and affect the solidity of the floor. Except for the extreme case where the temperature is brought to the level where the floor dissociates, the temperature does not affect solidity.

However, quantum mechanics can solve this problem. Heisenberg's uncertainty principle forces the electrons of the floor to be discrete values. This also means that the orbitals are incompressible unless the electrons can orbit in the same energy level (that is, possess non distinct quantum numbers). The Pauli Exclusion principle and Fermi-Dirac statistics show that this is also not a possibility, because electrons are fermions and therefore cannot occupy the same quantum state simultaneously.

So despite solidity being macroscopically observed, it is quantum mechanics that keeps solids from passing through each other.

Phase diagram of high temperature superconductors: chemically doped ceramics (magnetic insulators) to introduce mobile charge carriers.