Self-consistent Hartree-Fock approach to Phase Transitions

Hartree-Fock approach to Phase Transitions

Introduction to self consistent Hartree-Fock theory

The self consistent Hartree-Fock method is a way to approximately find the ground state of a many body system made of n interacting fermions. We start by writing the many particle wavefunction such that it respects the antisymmetry property of fermions. This is achieved by taking Slater determinant of one particle wave functions. The one particle wave functions Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left|i\right\rangle} can themselves be expressed in terms of the basis functions Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left|\chi_{k}\right\rangle} as

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left|i\right\rangle =\underset{k}{\sum}c_{ik}\left|\chi_{k}\right\rangle}

So, the Slater determinant is a function of the coefficients Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c_{ik}} .

In self consistent field theory, we make a guess for the form of the many electron ground state wave function and then use variation principle to calculate the best approximation for the ground state energy as a function of the coefficients. This leads to a set of non linear Hartree-Fock equations in terms of the coefficients. We then solve the equations iteratively to find the right values of the coefficients upto a certain accuracy. Thus, we obtain the self consistent solution for the ground state wave function of the n particle system and the ground state energy.

With the general introduction of self consistent Hartree-Fock method mentioned above, let us now elaborate on the topic with more mathematical details (the book used as reference for mathematical explanation is Quantum Mechanics by Eugen Merzbacher).

Consider a system of n interacting fermions. The Hamiltonian is expressed as

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H=\underset{\alpha\alpha'}{\sum}b_{\alpha}^{\dagger}\left\langle \alpha\left|H_{0}\right|\alpha'\right\rangle b_{\alpha'}+\frac{1}{2}\underset{\alpha\alpha'\beta\beta'}{\sum}b_{\alpha}^{\dagger}b_{\beta}^{\dagger}\left\langle \alpha\beta\left|V\right|\alpha'\beta'\right\rangle b_{\beta'}b_{\alpha'}}

The independent particle state can be written as

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left|\psi_{0}\right\rangle =a_{n}^{\dagger}a_{n-1}^{\dagger} ...a_{2}^{\dagger}a_{1}^{\dagger}\left|0\right\rangle}

In this basis,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H=\underset{i,j}{\sum}a_{i}^{\dagger}\left\langle i\left|H_{0}\right|j\right\rangle a_{j}+\frac{1}{2}\underset{qrst}{\sum a_{q}^{\dagger}a_{r}^{\dagger}\left\langle qr|V|ts\right\rangle a_{s}a_{t}}}

The variation of state Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left|\psi_{0}\right\rangle} is given by a linear combination

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta\psi_{jk}=\varepsilon_{jk}a_{j}^{\dagger}a_{k}\left|\psi_{0}\right\rangle}

The “best” state Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left|\psi_{0}\right\rangle} should minimise the ground state energy. Also, since H is Hermitian, therefore

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left\langle \psi_{0}|\psi_{0}\right\rangle \left\langle \delta\psi|H|\psi_{0}\right\rangle -\left\langle \psi_{0}|H|\psi_{0}\right\rangle \left\langle \delta\psi|\psi_{0}\right\rangle =0}

Further, since the variation preserves the fact that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left\langle \psi_{0}|\psi_{0}\right\rangle =1} , this makes Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left\langle \delta\psi_{0}|\psi_{0}\right\rangle =0} . Then the above equation reduces to

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left\langle \delta\psi|H|\psi_{0}\right\rangle =0}

Substituting the form of the variation and the Hamiltonian, we get

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left\langle j\left|H_{0}\right|k\right\rangle +\frac{1}{2}\underset{t}{\sum}[\left\langle jt\left|V\right|kt\right\rangle -\left\langle jt\left|V\right|tk\right\rangle ]=0}

Or, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H_{0}\left|m\right\rangle +\underset{p}{\sum}\left|p\right\rangle \underset{t}{\sum}[\left\langle pt\left|V\right|mt\right\rangle -\left\langle pt\left|V\right|tm\right\rangle ]=\varepsilon_{m}\left|m\right\rangle}

If Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left\langle \alpha\beta\left|V\right|\alpha'\beta'\right\rangle =V_{\alpha\beta}\delta_{\alpha\alpha'}\delta_{\beta\beta'}} then, we get

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H_{0}\left|m\right\rangle +\underset{t}{\sum}\underset{\alpha,\beta}{\sum}\left|\alpha\right\rangle \left\langle t\right|\left.\beta\right\rangle V_{\alpha\beta}[\left\langle \beta\right|\left.t\right\rangle \left\langle \alpha\right|\left.m\right\rangle -\left\langle \alpha\right|\left.t\right\rangle \left\langle \beta\right|\left.m\right\rangle ]=\varepsilon_{m}\left|m\right\rangle}

In matrix form, this can be written as

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \underset{\beta}{\sum}[\left\langle \alpha\right|H_{0}\left|\beta\right\rangle \left\langle \beta\right|\left.m\right\rangle +\underset{t}{\sum}\left\langle t\right|\left.\beta\right\rangle V_{\alpha\beta}[\left\langle \beta\right|\left.t\right\rangle \left\langle \alpha\right|\left.m\right\rangle -\left\langle \alpha\right|\left.t\right\rangle \left\langle \beta\right|\left.m\right\rangle ]]=\varepsilon_{k}\left\langle \alpha\right|\left.m\right\rangle}

This equation is known as Hartree-Fock equation. The first term in the summation over t on the left hand side of the above equation is known as the Hartree term or direct energy term. The last term in the sum is called the Fock term and it constitutes the exchange energy of the interaction between electrons.

The Hartree-Fock equations cannot be computed without knowing the n eigensolutions Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left|m\right\rangle} since the matrix elements of interaction term V depend on them. These equations are solved iteratively starting by guessing a set of one particle states Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left|m\right\rangle} to find the next set of eigensolutions. This set is compared with the previous set and if they don't match within error then the process is repeated till we get a self consistent set of eigensolutions.

Hartree-Fock in second quantized form for a two body system

The interaction energy operator for a two body system with pairwise interactions is given by

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \nu = \frac{1}{2} \sum_{\sigma \sigma^{\prime}} \int d^{3}r d^{3}r^{\prime} v(\vec{r}-\vec{r}^{ \prime}) \psi_{\sigma}^{\dagger}(\vec{r}) \psi_{\sigma^{\prime}}^{\dagger}(\vec{r}^{ \prime}) \psi_{\sigma^{\prime}}(\vec{r}^{ \prime}) \psi_{\sigma}(\vec{r}) }

In the above operator, it is important to note the order of the operators. Including the kinetic energy term we can write the Hamiltonian for particles of mass m with pairwise interactions in second quantized formalism as

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H = \sum_{\sigma \sigma^{\prime}} \int d^{3}r \frac{1}{2m} \nabla \psi_{\sigma}^{\dagger}(\vec{r}) \cdot \nabla \psi_{\sigma}(\vec{r}) + \frac{1}{2} \sum_{\sigma \sigma^{\prime}} \int d^{3}r d^{3}r^{\prime} v(\vec{r}-\vec{r}^{ \prime}) \psi_{\sigma}^{\dagger}(\vec{r}) \psi_{\sigma^{\prime}}^{\dagger}(\vec{r}^{ \prime}) \psi_{\sigma^{\prime}}(\vec{r}^{ \prime}) \psi_{\sigma}(\vec{r}) }

The first-order correction to the energy induced by the interaction is

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E^{(1)} = \frac{1}{2}\int d^{3}rd^{3}r^{\prime}v(\vec{r} - \vec{r}^{\prime})\sum_{\sigma\sigma^{\prime}}<\Phi_{0}|\psi_{\sigma}^{\dagger}(\vec{r}) \psi_{\sigma^{\prime}}^{\dagger}(\vec{r}^{ \prime}) \psi_{\sigma^{\prime}}(\vec{r}^{ \prime}) \psi_{\sigma}(\vec{r})|\Phi_{0}>}

Define Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G_{\sigma}(\vec{r}-\vec{r}^{\prime})= <\Phi_{0}|\psi_{\sigma}^{\dagger}(\vec{r})\psi_{\sigma}(\vec{r}^{\prime})|\Phi_{0}>}

Then, we find that

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E^{(1)} = \frac{1}{2}\int d^{3}r d^{3}r^{\prime} v(\vec{r}-\vec{r}^{ \prime})[n^{2}-\sum_{\sigma}G_{\sigma}(\vec{r}-\vec{r}^{\prime})^{2}]}

(You can find intermediate steps in "Lectures on Quantum Mechanics" by Gordon Baym).

The first term in Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E^{(1)}} is called the Hartree energy or direct energy. The second term is called the Fock term and it corresponds to the energy due to exchange interactions.

Examples

Electron Gas Phase Transition

For an interacting electron gas, the electron-electron interaction V is diagonal in coordinate representation -

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V\left(\vec{r}\sigma,\vec{r'}\sigma'\right)=\frac{e^{2}}{\left|\vec{r}-\vec{r'}\right|}}

Then, in coordinate representation with Hartree-Fock eigenfunctions denoted as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left\langle \vec{r}\sigma\right|\left.m\right\rangle =\psi_{m}\left(\vec{r}\sigma\right)} the Hartree-Fock equations become

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{-\hbar^{2}}{2m}\nabla^{2}\psi_{m}\left(\vec{r}\sigma\right)-\frac{Ze^{2}}{r}\psi_{m}\left(\vec{r}\sigma\right)+e^{2}\underset{t}{\sum}\underset{\sigma'}{\sum}\int\psi_{t}^{*}(\vec{r'}\sigma')\frac{1}{\left|\vec{r}-\vec{r'}\right|}\psi_{m}\left(\vec{r}\sigma\right)d^{3}r'-e^{2}\underset{t}{\sum}\underset{\sigma'}{\sum}\int\psi_{t}^{*}\left(\vec{r'}\sigma'\right)\frac{1}{\left|\vec{r}-\vec{r'}\right|}\psi_{t}\left(\vec{r}\sigma\right)\psi_{m}\left(\vec{r'}\sigma'\right)d^{3}r'=\varepsilon_{m}\psi_{m}\left(\vec{r}\sigma\right)}

or, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [\frac{-\hbar^{2}}{2m}\nabla_{r}^{2}+V_{ion}(r)+e^{2}\underset{\lambda}{\sum}\int d\vec{r'}n_{\psi_{\lambda}}\left(r'\right)\frac{1}{\left|\vec{r}-\vec{r'}\right|}]\psi_{m}(\vec{r})-e^{2}\underset{\lambda}{\sum}\int d\vec{r'}\psi_{m}(\vec{r'})\psi_{\lambda}^{*}(\vec{r'})\psi_{\lambda}(\vec{r})\frac{1}{\left|\vec{r}-\vec{r'}\right|}=\varepsilon_{m}\psi_{m}\left(\vec{r}\sigma\right)}

We see that plane-wave states satisfy the above equation and we obtain the eigenvalue equation,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon(\vec{k})\psi_{\vec{k}}(\vec{r})=[k^{2}+V_{ion}\left(r\right)+ e^{2}n_{e}\int d\vec{r'}\frac{1}{\left|\vec{r}-\vec{r'}\right|}]\psi_{\vec{k}}(\vec{r})-\int\frac{d\vec{q}d\vec{x}}{(2\pi)^{3}}\frac{e^{i(\vec{k}-\vec{q}).\vec{x}}}{\left|\vec{x}\right|}\psi_{\vec{k}}(\vec{r})}

where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{x}=\vec{r}-\vec{r'}} .

Due to charge neutrality constraint,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_{ion}(\vec{r})=\underset{i}{\sum}\frac{-Ze^{2}}{\left|\vec{r}-\vec{R_{i}}\right|}\rightarrow-n_{e}\int\frac{d\vec{R}}{\left|\vec{r}-\vec{R}\right|}}

and hence, the second and the third term in the eigen equation cancel each other. Then,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon(\vec{k})=k^{2}-\int_{0}^{k_{f}}\frac{d\vec{q}}{(2\pi)^{3}}\int d\vec{x}\frac{e^{i(\vec{k}-\vec{q}).\vec{x}}}{\left|\vec{x}\right|}=k^{2}-\epsilon_{exch}(\vec{k})}

where, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon_{exch}(\vec{k})} is the single-particle exchange energy.

Solving the integral over Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle d\vec{x}} in Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon_{exch}(\vec{k})} we get,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon_{exch}(\vec{k})=\frac{-1}{\pi^{2}}\int d\vec{q}\frac{\theta(\mu-\epsilon(\vec{q}))}{\left|\vec{k}-\vec{q}\right|^{2}}}

From here, we will closely follow the work of Gartenhaus and Stranahan.

It can be shown that an electron gas will undergo a first-order phase transition at a critical value of the chemical potential. At this value, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu_{0}} , the particle density Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n(\mu)} experiences a finite discontinuity. In units of Rydbergs, the energy of a single electron using Hartree-Fock is

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon(k) = k^{2} - \frac{1}{\pi^{2}}\int d^{3}q \frac{1}{\left(\vec{q} - \vec{k}\right)^{2} + \lambda^{2}} \theta(\mu - \epsilon(\vec{q})) \quad\quad(1)}

where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda} has been introduced to avoid any divergences and is called the shielding parameter. The above equation may have multiple solutions for a given set of values for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu} , and it is this property that will give rise to a discontinuity in the particle density. In the case of multiple solutions, the correct choice is the one that minimizes the free energy.

Define

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E(k,k_{0}) = k^{2} - \frac{1}{\pi^{2}}\int d^{3}q \frac{1}{\left(\vec{q} - \vec{k}\right)^{2} + \lambda^{2}} \theta(k_{0} - q) \quad\quad(2)}

where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k_{0}} is often called the radius of the Fermi sphere and is determined by the equation

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E(k_{0},k_{0}) = \mu \quad\quad(3)}

Equation (2) is a solution to (1) provided that

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial}{\partial k}E(k,k_{0}) > 0}

The formula for the particle density function is

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n(\mu) = \frac{2}{(2\pi)^{3}} \int d^{3}k \theta(\mu - \epsilon(\vec{k})) \quad\quad(4)}

Source: Gartenhaus and Stranahan

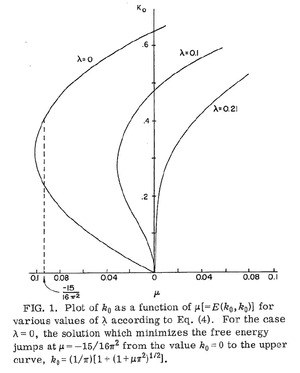
If $\mu <0$, then $n(\mu )=0$ according to (4), and a solution to (1) is

$\epsilon (k)=k^{2}\$

For other values of $\mu$,

$n(\mu )={\frac {k_{0}^{3}}{3\pi ^{2}}}$

The number of solutions provided by (2) is equal to the number of values of $k_{0}$ which solve (3). The correct solution is found by minimizing the free energy, given by

$F(\mu )=-\int _{-\infty }^{\mu }n(\mu )d\mu =-{\frac {1}{3\pi ^{2}}}\int _{0}^{\mu }k_{0}^{3}d\mu \quad \quad (5)$

When $\lambda >0.21$, there is only one value of $k_{0}$ for a given chemical potential. However, for smaller values of $\lambda$, there are multiple solutions for $k_{0}$, as shown in the figure to the right. Consider the case when $\lambda =0$. By minimizing (5) to determine the correct solution for a given $\mu$, we find that the solution to $k_{0}$ changes discontinuously at around $\mu _{0}=-15/16\pi ^{2}$:

$k_{0}=0\ \ ,\quad \mu <-{\frac {15}{16\pi ^{2}}}$

$k_{0}={\frac {1}{\pi }}+\left({\frac {1}{\pi ^{2}}}+\mu \right)^{\frac {1}{2}}\ \ ,\quad \mu >-{\frac {15}{16\pi ^{2}}}$

The discontinuity in the solution of $k_{0}$ corresponds directly to a discontinuity in the particle density, and so a first-order phase transition occurs around $\mu _{0}=-15/16\pi ^{2}$:

$n(\mu )=0\ \ ,\quad \mu <-{\frac {15}{16\pi ^{2}}}$

$n(\mu )={\frac {1}{3\pi ^{2}}}\left[{\frac {1}{\pi }}+\left({\frac {1}{\pi ^{2}}}+\mu \right)^{\frac {1}{2}}\right]^{3}\ \ ,\quad \mu >-{\frac {15}{16\pi ^{2}}}$

Phase transitions in N-electron atoms at large dimension limit

Briefly presented below is work by Pablo Serra and Sabre Kais using the Hartree-Fock theory to estimate the symmetry breaking in N-electron atoms at the large density ($D\rightarrow \infty$) limit.

Source: Serra and Kais

Source: Serra and Kais

Source: Serra and Kais

Source: Serra and Kais

In the large dimension limit, the dimensional-scaled effective Hamiltonian for Hartree-Fock N-electron atoms is obtained by the constraint that the interelectronic angles become fixed at $90^{\circ }C$

${\mathcal {H}}_{\infty }={\frac {1}{2}}{\underset {i=1}{\overset {N}{\Sigma }}}{\frac {1}{\rho _{i}{}^{2}}}-Z{\underset {i=1}{\overset {N}{\Sigma }}}{\frac {1}{\rho _{i}}}+{\underset {i=1}{\overset {N-1}{\Sigma }}}{\underset {j=i+1}{\overset {N}{\Sigma }}}{\frac {1}{\left(\rho _{i}{}^{2}+\rho _{j}{}^{2}\right){}^{1/2}}}$

where $\rho _{i}$ are the electron-nucleus radii and Z is the nuclear charge. The large-D limit ground-state energy is given by

$E_{\infty }(N,Z)={\underset {\left\{\rho _{i}\right\}}{min{\mathcal {H}}_{\infty }}}$

yielding the set of equations

${\frac {-1}{\rho _{i}{}^{3}}}+{\frac {Z}{\rho _{i}{}^{2}}}-\rho _{i}{\underset {j\neq i}{\Sigma }}{\frac {1}{\left(\rho _{i}{}^{2}+\rho _{j}{}^{2}\right){}^{3/2}}}=0,{\text{ }}i=1,2,{\text{...}},N$.

A symmetric solution is when all N electrons are equidistant from the nucleus, with

$\rho _{i}=\rho ={\frac {2^{2/3}}{\left(2^{2/3}Z-N+1\right)}}$.

with energy given by

$E_{\infty }{}^{\text{sym}}(N,Z)={\frac {-N}{2}}\left(Z-{\frac {N-1}{2^{3/2}}}\right)^{2}$

In the case of N-electrons, the symmetry breaking does not coincide with the stability limit of the symmetric phase point, as it would for N=2. For NFailed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \neq } 2, a region has been discovered with more than one local minima indicating a phase coexistence region in mean field theories. The first-order phase transition appears when the global minimum degenerates. The symmetric phase occurs when all electrons are equidistant from the nucleus. For small values of N, this symmetry may be broken by removing one electron to a much larger distance, leaving a core of N-1 electrons, equivalent to saying

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho _1=\rho _2\text{=.}\text{..}=\rho _{N-1}=\rho ,\text{ }\rho _N=(1+\eta )\rho \quad (Phase A_{1}) \ }

where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \eta \neq 0} . This is stable for small Z values, but there is a coexistence region with the symmetric solution with both being minimas of the variational equations. For fixed N,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_{\infty }{}^{\text{sym}}\left(N,Z_1\right)=E_{\infty }{}^{\left(A_1\right)}\left(N,Z_1\right)}

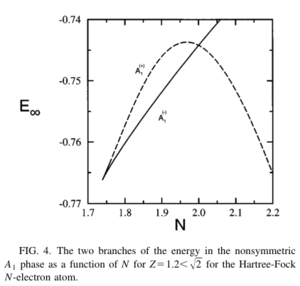
gives the first-order phase transition point Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z_1} with the right hand side giving the energy in phase Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A_1} . Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \eta} in the above equation is not restricted except that it Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \eta \neq 0} , with positive and negative values giving a different energy on the right hand side. NFailed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle >} 2 corresponds to the global minimum when Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \eta >0} , while for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle N<2} the global minimum corresponds to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \eta <0} . In Figure [4], the two energies for these phases cross at N=2, indicating a first-order phase transition line with critical point

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z_c=\sqrt{2}} .

For Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle N>2} , the equations give

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \underset{Z\to N-1}{\text{Lim}}\eta =\infty}

while Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho} remains finite so

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \underset{Z\to N-1}{\text{Lim}}\rho _N=\infty }

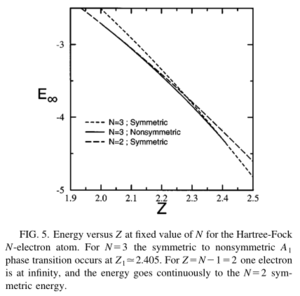
With one electron removed to infinite distance, one must identify the point (N-1,Z) with the point (N,Z). One can see in Figure [5] the global minimum for Z changes phases with Z. In this work, the processes studied are ionization and electron affinity processes connected with neutral atoms occurring in the region where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle N\leq Z\leq N+1} . For values of N less than Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle N_1=12.177} for neutral atoms the symmetric state provides the global minimum. Above this value, the nonsymmetric phase Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A_1} is the global minimum. New non-symmetric electronic configurations must be considered. First Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A_1} is generalized to $A_{m}$. These phases are defined by removing m electrons significantly far from the nucleus. Also a nonsymmetric phase, phase B, is introduced as

$\rho _{1}{\text{=.}}{\text{..}}=\rho _{N-2}=\rho ,{\text{ }}\rho _{N-1}=(1+\mu )\rho ,{\text{ }}\rho _{N}=(1+\eta )\rho \$

For $Z>Z_{B}$ where $Z_{B}$ is defined by

$E_{\infty }{}^{\left(A_{1}\right)}\left(N,Z_{B}\right)=E_{\infty }{}^{(B)}\left(N,Z_{B}\right)$

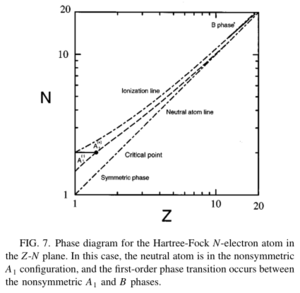
with $N_{1}<N<N_{2}\simeq 27.45$ starting from neutral atoms, the nonsymmetric phase is the global minimum. At this point, there is a phase transition between $A_{1}$ and B where the symmetry breaking is resultant from the removal of one electron to complete ionization in the limit where $Z\to N-1$. Here the system undergoes another phase change but with N-1 electrons instead (Figure 7).

At this point we will move to the discussion on the effect of a weak external electric field on phase transitions and symmetry breaking for these N-electron atoms. The effective Hamiltonian in a weak electric field looks like

${\mathcal {H}}_{\infty }(N,Z,{\mathcal {E}})={\mathcal {H}}_{\infty }(N,Z)-{\mathcal {E}}\left({\underset {i=1}{\overset {N-1}{\Sigma }}}\rho _{i}-\rho _{N}\right)$

where ${\mathcal {H}}_{\infty }(N,Z)$ as discussed above is now modified by the applied electric field. If we define a new order parameter

$\psi \equiv {\frac {\rho _{N}-\rho _{1}}{\rho _{>}}}=\left\{{\begin{array}{cc}\eta ,&\eta <0\\{\frac {\eta }{1+\eta }},&\eta >0\end{array}}\right.$

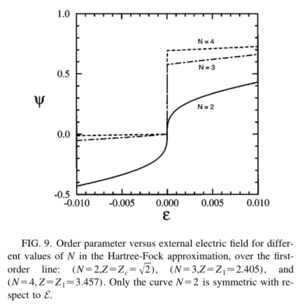
and plot vs. ${\mathcal {E}}$, nonsymmetric curves for $N>2$ are observed (Figure[9]).