Bose Hubbard model: Difference between revisions
| (28 intermediate revisions by the same user not shown) | |||
| Line 137: | Line 137: | ||
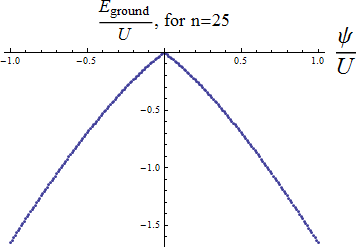
For any given value of <math>\mu</math> and <math>U</math>, we can numerically minimize the quantum expectation of the energy <math>\left\langle \Phi _{\text{trial}}|\mathcal{H}|\Phi _{\text{trial}}\right\rangle</math> with respect to <math>\psi</math>. The result exposes a phase transition: some regions of the <math>\frac{\mu }{U}-\frac{t}{U}</math> plane give a minimum energy at <math>\psi = 0</math> and some do not. In the former case, our Bose Hubbard system is a Mott insulator, in the latter it exhibits superconductivity. In figure 4 we can see the rounded "Mott lobes" for which the system is an insulator. | For any given value of <math>\mu</math> and <math>U</math>, we can numerically minimize the quantum expectation of the energy <math>\left\langle \Phi _{\text{trial}}|\mathcal{H}|\Phi _{\text{trial}}\right\rangle</math> with respect to <math>\psi</math>. The result exposes a phase transition: some regions of the <math>\frac{\mu }{U}-\frac{t}{U}</math> plane give a minimum energy at <math>\psi = 0</math> and some do not. In the former case, our Bose Hubbard system is a Mott insulator, in the latter it exhibits superconductivity. In figure 4 we can see the rounded "Mott lobes" for which the system is an insulator. | ||
In fact (though this cannot be seen in the figure), the numerical calculation shows that this is a second order phase transition. That is, as we travel from the boundary of a Mott lobe in the <math>\frac{\mu }{U}-\frac{t}{U}</math> plane, <math>psi</math> ramps up smoothly from zero without any discontinuous jumps. | In fact (though this cannot be seen in the figure), the numerical calculation shows that this is a second order phase transition. That is, as we travel from the boundary of a Mott lobe in the <math>\frac{\mu }{U}-\frac{t}{U}</math> plane, <math>\psi</math> ramps up smoothly from zero without any discontinuous jumps. | ||
==Analytic Description of the Phase Transition== | ==Analytic Description of the Phase Transition== | ||
| Line 144: | Line 144: | ||
To expose the difference between the two phases, it is helpful to consider two limiting cases. | To expose the difference between the two phases, it is helpful to consider two limiting cases. | ||
First Consider <math>t=0</math>. Here we have a zero amplitude for hopping, so all particles are pinned to their respective sites. In fact, this is just the [[#PsiZeroAnchor|<math>\psi = 0</math> case]] we considered earlier, and the ground state occupation numbers are just <math>\left\lceil \frac{\mu }{U}\right\rceil </math> for every lattice site provided that <math>\frac{\mu }{U}</math> is not an integer. | First Consider <math>t=0</math>. Here we have a zero amplitude for hopping, so all particles are pinned to their respective sites. In fact, this is just the [[#PsiZeroAnchor|<math>\psi = 0</math> case]] we considered earlier, and the ground state occupation numbers are just <math>\left\lceil \frac{\mu }{U}\right\rceil </math> for every lattice site provided that <math>\frac{\mu }{U}</math> is not an integer. Here, regardless of the system size, there is a finite energy gap between the ground state and the next excited state (where all but two of the occupation numbers are equal). This is a characteristic of the Mott insulator phase. | ||
In the opposite scenario, <math>U=0</math>, and the Hamiltonian can be diagonalized in a basis consisting of the Fourier transform of the <math>b_{i,j}</math> operators: | In the opposite scenario, <math>U=0</math>, and the Hamiltonian can be diagonalized in a basis consisting of the Fourier transform of the <math>b_{i,j}</math> operators: | ||
<math>\mathcal{H} = \sum _{r,l} \left(\epsilon _{r,l }-\mu \right)d_{r,l}^{\dagger } d_{r,l}\text{ }\left(\text{for } d_{r,l}\propto \sum _{j,k} e^{-i \frac{2\pi }{N}\{j r+k l\}}a_{j,k}\right)</math> | <math>\mathcal{H} = \sum _{r,l} \left(\epsilon _{r,l }-\mu \right)d_{r,l}^{\dagger } d_{r,l}\text{ }\left(\text{for } d_{r,l}\propto \sum _{j,k} e^{-i \frac{2\pi }{N}\{j r+k l\}}a_{j,k}\right)</math> | ||
In this limit our eigenstates are completely delocalized. Furthermore, there is a unique minimum energy state with <math>r=l=0</math>. Thus at low temperature we will have Bose-Einstein condensation sharply peaked in momentum space. | In this limit our eigenstates are completely delocalized. Furthermore, there is a unique minimum energy state with <math>r=l=0</math>. Thus at low temperature we will have Bose-Einstein condensation sharply peaked in momentum space. Finally, there is no energy gap in the limit of infinite system size, since the allowed momentum values <math>\left(\frac{r 2\pi }{N} \text{ and } \frac{l 2\pi }{N}\right)</math> will become arbitrarily close to the ground state values. These are characteristics of the superfluid phase. | ||
===Symmetries=== | ===Symmetries=== | ||
The reason for | The reason for taking <math>\psi</math> as our order parameter for the phase transition can be seen by considering symmetries. First of all, it is clear that our [[#HamiltonianAnchor|Bose Hubbard Hamiltonian]] has a <math>U(1)</math> phase rotation symmetry where every <math>b_{i,j} \longrightarrow b_{i,j}e^{i \phi }</math>. In the localized limit we see an extended form of this symmetry: the Hamiltonian is invariant under different phase rotations for every site. In the delocalized limit, we have the opposite behavior. Whereas for the <math>t=0</math> case the Hamiltonian didn't prioritize any given phase distribution among the particles, in the <math>U=0</math> case it minimizes the energy of the state where all <math>b</math>'s have the same phase (see the expression above for <math>d_{0,0}</math>). This is a hint that the ground states with a non-zero <math>U(1)</math> symmetry-breaking <math>\psi</math> field will be more similar to the <math>U=0</math> case. | ||
===Ground State Occupation=== | |||
Another way to look at the two different phases is by considering the occupation number <math>\hat{N}_b=\sum _{i,j} b_{i,j}^{\dagger }b_{i,j}</math> for the ground state. The <math>t=0</math> Hamiltonian clearly commutes with <math>\hat{N}_b</math>. Interestingly, as <math>t</math> is brought up slowly from zero, this perturbed Hamiltonian also commutes with <math>\hat{N}_b</math>. As a result, every non-degenerate ground state (i.e. non-integer <math>\frac{\mu}{U}</math> state) on the phase plane at <math>t=0</math>, which is an exact eigenstate of <math>\hat{N}_b</math> with eigenvalue <math>N^2 \left\lceil \frac{\mu }{U}\right\rceil </math>, moves adiabatically into another eigenstate of <math>\hat{N}_b</math> with the same eigenvalue. There is no level crossing for at least some region (which turns out to be the Mott lobe) because our original state was separated with a finite energy gap. Thus the new state at <math>t\neq0</math> is still the ground state. By translation symmetry, every site is the same, so the expectation value for any site is <math>\left\lceil \frac{\mu }{U}\right\rceil </math>, just like at <math>t=0</math>. | |||
The preceding argument does not work at values of <math>\mu</math> for which there is a ground state degeneracy at <math>t=0</math>. We can see in figure 4 that these points on the phase plane border the superfluid region. | |||
<span id="ExperimentAnchor"></span> | <span id="ExperimentAnchor"></span> | ||
Latest revision as of 01:45, 15 December 2012
Introduction
The Bose-Hubbard Model (BHM) was first studied in theoretical detail in 1989 by Fisher et al.[1]
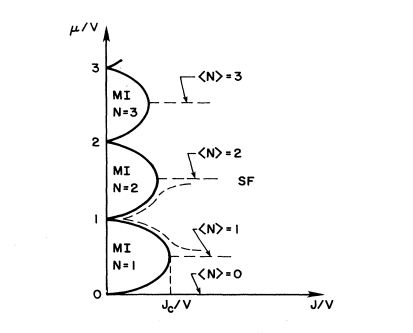
It was discovered that at zero temperature if the bosons are in a lattice they can be in one of two phases. The phase diagram in figure 1 shows this explicitly: there is the superfluid phase and the Mott insulator phase. The phase the system is in depends on the strength of the hopping interaction(J in the figure 1, 4t in our analysis) as well as the chemical potential Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu} (which sets the particle number) and the on site repulsion (V in figure 1, U in our analysis).
The Bose Hubbard Hamiltonian
The Bose Hubbard model Hamiltonian, on an Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle N\times N} 2 dimensional grid, is given by the expression
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{array}{c} \mathcal{H}= -t \sum _{i=1}^N \sum _{j=1}^N \left(b_{i,j}^{\dagger }b_{i+1,j}+b_{i,j}^{\dagger }b_{i,j+1}+b_{i+1,j}^{\dagger }b_{i,j}+b_{i,j+1}^{\dagger }b_{i,j}\right) \\ +\frac{U}{2}\sum _{i=1}^N \sum _{j=1}^N b_{i,j}^{\dagger }b_{i,j}\left(b_{i,j}^{\dagger }b_{i,j}-1\right)-\mu \sum _{i=1}^N \sum _{j=1}^N b_{i,j}^{\dagger } b_{i,j} \end{array} }
Here the creation and annihilation operators obey Bose commutation relations Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left[b_i,b_j{}^{\dagger }\right]=\delta _{i,j}} . The spinless bosons can represent Cooper pairs of electrons undergoing Josephson tunneling between superconducting islands[2], or atoms in an optical lattice. If the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{H}} is taken to describe cooper pairs, it is clear that the decay of the pair into two electrons can not be modeled in our formalism.
Mean Field Theory Solution For The Ground State
Single Site Hamiltonian
The single site Hamiltonian for interacting bosons is:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{H}_{\text{site}}= \frac{U}{2}b^{\dagger }b \left(b^{\dagger }b-\mathbf{1}\right)- \mu b^{\dagger }b\text{ }+ \left(\psi^{*}b +b^{\dagger }\psi\right)}
Where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U > 0, \mu \geq 0} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi^{*}} are c-numbers. Here, the field Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi} is meant to stand for the average of the influence of all neighboring sites.
Solution For Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi = \psi^{*}=0}
In this case the Hamiltonian can be rewritten as:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{H}_{\text{site}}= \frac{U}{2}b^{\dagger }b \left(b^{\dagger }b-\mathbf{1}\right)- \mu b^{\dagger }b = \frac{U}{2}b^{\dagger }b\text{ }\left(b^{\dagger }b - \left(1+2 \frac{\mu }{U}\right)\mathbf{1} \right)} .
Unnormalized eigenstates of this Hamiltonian areFailed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |n\rangle}
.
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{H}_{\text{site}}|n\rangle = \frac{U}{2}b^{\dagger }b\text{ }\left(b^{\dagger }b |n\rangle - \left(1+2 \frac{\mu }{U}\right)|n\rangle \right)= \frac{U}{2}\text{ }\left(n^2- \left(1+2 \frac{\mu }{U}\right)n\right)|n\rangle} .
The normalized eigenstate is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{\sqrt{n!}}|n\rangle} with eigenenergy Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_n =\frac{U}{2}\text{ }\left(n^2- \left(1+2 \frac{\mu }{U}\right)n\right)} .
We minimize the previous expression for energy to find that the ground state is unique for the ratio Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\mu}{U} \notin \mathbb{Z}} ; it is equal to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left\lceil \frac{\mu }{U}\right\rceil} , the closest integer larger than Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\mu }{U}} . On the other hand, we have a two-fold degeneracy for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\mu}{U} \in \mathbb{Z}} .
Solution For Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi \neq 0} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi \in \mathbb{R}}
Now that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi } is included lets redefine our states to be Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |j\rangle = \frac{1}{\sqrt{j!}}b^{\dagger j}|0\rangle} . The Hamiltonian is now:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{H}_{\text{site}}= \frac{U}{2}b^{\dagger }b \left(b^{\dagger }b-\mathbf{1}\right)- \mu b^{\dagger }b\text{ }+\psi \left(b +b^{\dagger }\right)} .
The goal of this section is to treat the site as capable of holding only a finite number Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n} of particles. We shall derive a self-consistent matrix equation for the ground state for a given value of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi} . Because the matrix is finite, we can then solve numerically.
Acting on Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{H}_{\text{site}}} with some general state Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\phi \rangle =\sum _{j=0}^n c_j|j\rangle} , we have:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left\langle i\left|\mathcal{H}_{\text{site}}-E \right|\phi \right\rangle =0}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Longrightarrow \sum _{j=0}^n c_j\left\langle i\left|\frac{U}{2}b^{\dagger }b \left(b^{\dagger }b-\mathbf{1}\right)- \mu b^{\dagger }b\text{ }+\psi \left(b +b^{\dagger }\right)-E \mathbf{1} \right|j\right\rangle = 0}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Longrightarrow \sum _{j=0}^n c_j\langle i|\left\{\frac{U}{2}j (j-1) |j\rangle - \mu j\text{ }|j\rangle \text{ }-E\text{ }|j\rangle +\psi \left(\sqrt{j} |j-1\rangle +\sqrt{j+1}|j+1\rangle \right)\right\}=0}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Longrightarrow \sum _{j=0}^n c_j\left\{\delta _{i ,j}\left[\frac{U}{2}j (j-1) - \mu j\text{ }-E\right]+\delta _{i ,j-1} \left[\psi \sqrt{j}\text{ }\right]+\delta _{i,j+1\text{ }}\left[\psi \sqrt{j+1}\right]\text{ }\right\}=0}
For Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i=0} we have
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -c_0\frac{E}{U}+ c_1 \frac{\psi }{U}\text{ }= 0} .
For Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i=n} we have
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c_n\overbrace{\left[\frac{1}{2}n (n-1) - \frac{\mu }{U} n -\frac{E}{U}\right]}^{\equiv D(n)}+c_{n-1}\left[\frac{\psi }{U}\sqrt{n}\right]\text{ }=0}
Defining a function Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D[i] = \frac{1}{2}i (i-1) - \frac{\mu }{U} i -\frac{E}{U}} , we can write the above in matrix form:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left( \begin{array}{cccccccc} D(0) & \frac{\psi }{U} & 0 & 0 & 0 & \cdots & \cdots & 0 \\ \frac{\psi }{U} & D(1) & \frac{\psi }{U} \sqrt{1+1} & 0 & 0 & \cdots & \cdots & 0 \\ 0 & \frac{\psi }{U} \sqrt{2} & D(2) & \frac{\psi }{U} \sqrt{2+1} & 0 & \cdots & \cdots & 0 \\ 0 & 0 & \frac{\psi }{U} \sqrt{3} & D(3) & \frac{\psi }{U} \sqrt{3+1} & \cdots & \cdots & 0 \\ 0 & 0 & 0 & \frac{\psi }{U} \sqrt{4} & D(4) & \ddots & & \\ \vdots & \vdots & \vdots & \vdots & \vdots & \ddots & \ddots & \\ \vdots & \vdots & \vdots & \vdots & \vdots & \ddots & \ddots & \ddots \\ 0 & 0 & 0 & 0 & 0 & & \frac{\psi }{U}\sqrt{n} & D(n) \end{array} \right)\left( \begin{array}{c} c_0 \\ c_1 \\ c_2 \\ c_3 \\ c_4 \\ c_5 \\ \vdots \\ c_n \end{array} \right)=0}
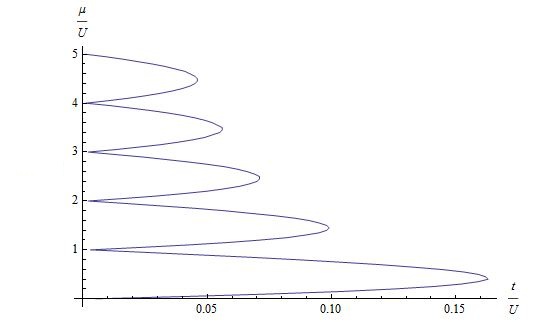
Example solutions to the preceding equation can be seen in figure 3.
An important check on the consistency of our work up to here is that the size of the coefficients Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c_j} approach zero as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle j} approaches Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n} . Were this not the case, our assumption of the site's finite potential occupancy would have been unwarranted. In the example displayed, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c_n} was on the order of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 10^{-7}} .
Multi-Site Square Lattice Hamiltonian
By adding and subtracting the mean-field terms from all sites in the original Bose Hubbard Hamiltonian Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{H}} , we can write:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{H} =\text{ }- t \sum _{i=1}^N \sum _{j=1}^N \left(b_{i,j}^{\dagger }b_{i+1,j}+b_{i,j}^{\dagger }b_{i,j+1} + b_{i+1,j}^{\dagger }b_{i,j}+b_{i,j+1}^{\dagger }b_{i,j} +\frac{\psi }{t}\left(b_{i,j} +b_{i,j}^{\dagger }\right)\right)+ \sum _{i=1}^N \sum _{j=1}^N b_{i,j}^{\dagger }b_{i,j}\left(\frac{U}{2}b_{i,j}^{\dagger }b_{i,j}-\frac{U}{2} - \mu \right)+\psi \sum _{i=1}^N \sum _{j=1}^N \left(b_{i,j} +b_{i,j}^{\dagger }\right)}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle =\overbrace{- t \sum _{i=1}^N \sum _{j=1}^N \left(b_{i,j}^{\dagger }b_{i+1,j}+b_{i,j}^{\dagger }b_{i,j+1} + b_{i+1,j}^{\dagger }b_{i,j}+b_{i,j+1}^{\dagger }b_{i,j} +\frac{\psi }{t}\left(b_{i,j} +b_{i,j}^{\dagger }\right)\right)}^{\equiv \overset{1}{\mathcal{H}}}+ \overbrace{\sum _{i=1}^N \sum _{j=1}^N \mathcal{H}_{i,j}(\psi ,\mu ,U)}^{\equiv \overset{2}{\mathcal{H}}}}
We will look at the second part first. Here Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \overset{2}{\mathcal{H}}} is just a sum over the single-site mean field Hamiltonians that we considered earlier. To take advantage of the single-site solution already in hand, we define the trial state as:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left|\Phi _{\text{trial}}\right\rangle = \overset{\otimes }{\underset{i,j}{\Pi }}\phi (i,j) = \overset{\otimes }{\underset{i,j}{\Pi }}\sum _{m=0}^n c_m(i,j) |m\rangle _{i,j}}
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |m\rangle _{i,j}} denotes bosons at lattice site . In the trial state the are the same for every and and are equal to the values we found numerically in the previous section. In fact the are dependent on the same parameters as the ground state energy, namely (, , and ); however, this dependence is kept implicit in the interest of readability. Keeping these facts in mind, we see that
where is the ground state eigenenergy from the single site case.
We can (somewhat tediously) work out in terms of the (fixed!) coefficients by operating the creation/annihilation operators that make up the definition of on the of the trial state. After a re-indexing and combining terms we come to our final result:
Phase Transition
For any given value of and , we can numerically minimize the quantum expectation of the energy with respect to . The result exposes a phase transition: some regions of the plane give a minimum energy at and some do not. In the former case, our Bose Hubbard system is a Mott insulator, in the latter it exhibits superconductivity. In figure 4 we can see the rounded "Mott lobes" for which the system is an insulator.
In fact (though this cannot be seen in the figure), the numerical calculation shows that this is a second order phase transition. That is, as we travel from the boundary of a Mott lobe in the plane, ramps up smoothly from zero without any discontinuous jumps.
Analytic Description of the Phase Transition
Limiting Cases:
To expose the difference between the two phases, it is helpful to consider two limiting cases.
First Consider Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t=0} . Here we have a zero amplitude for hopping, so all particles are pinned to their respective sites. In fact, this is just the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi = 0} case we considered earlier, and the ground state occupation numbers are just Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left\lceil \frac{\mu }{U}\right\rceil } for every lattice site provided that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\mu }{U}} is not an integer. Here, regardless of the system size, there is a finite energy gap between the ground state and the next excited state (where all but two of the occupation numbers are equal). This is a characteristic of the Mott insulator phase.
In the opposite scenario, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U=0} , and the Hamiltonian can be diagonalized in a basis consisting of the Fourier transform of the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b_{i,j}} operators: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{H} = \sum _{r,l} \left(\epsilon _{r,l }-\mu \right)d_{r,l}^{\dagger } d_{r,l}\text{ }\left(\text{for } d_{r,l}\propto \sum _{j,k} e^{-i \frac{2\pi }{N}\{j r+k l\}}a_{j,k}\right)}
In this limit our eigenstates are completely delocalized. Furthermore, there is a unique minimum energy state with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r=l=0} . Thus at low temperature we will have Bose-Einstein condensation sharply peaked in momentum space. Finally, there is no energy gap in the limit of infinite system size, since the allowed momentum values Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(\frac{r 2\pi }{N} \text{ and } \frac{l 2\pi }{N}\right)} will become arbitrarily close to the ground state values. These are characteristics of the superfluid phase.
Symmetries
The reason for taking Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi} as our order parameter for the phase transition can be seen by considering symmetries. First of all, it is clear that our Bose Hubbard Hamiltonian has a Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U(1)} phase rotation symmetry where every Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b_{i,j} \longrightarrow b_{i,j}e^{i \phi }} . In the localized limit we see an extended form of this symmetry: the Hamiltonian is invariant under different phase rotations for every site. In the delocalized limit, we have the opposite behavior. Whereas for the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t=0} case the Hamiltonian didn't prioritize any given phase distribution among the particles, in the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U=0} case it minimizes the energy of the state where all Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b} 's have the same phase (see the expression above for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle d_{0,0}} ). This is a hint that the ground states with a non-zero Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U(1)} symmetry-breaking Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi} field will be more similar to the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U=0} case.
Ground State Occupation
Another way to look at the two different phases is by considering the occupation number Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{N}_b=\sum _{i,j} b_{i,j}^{\dagger }b_{i,j}} for the ground state. The Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t=0} Hamiltonian clearly commutes with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{N}_b} . Interestingly, as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t} is brought up slowly from zero, this perturbed Hamiltonian also commutes with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{N}_b} . As a result, every non-degenerate ground state (i.e. non-integer Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\mu}{U}} state) on the phase plane at Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t=0} , which is an exact eigenstate of with eigenvalue , moves adiabatically into another eigenstate of with the same eigenvalue. There is no level crossing for at least some region (which turns out to be the Mott lobe) because our original state was separated with a finite energy gap. Thus the new state at is still the ground state. By translation symmetry, every site is the same, so the expectation value for any site is , just like at .
The preceding argument does not work at values of for which there is a ground state degeneracy at . We can see in figure 4 that these points on the phase plane border the superfluid region.
Experimental Evidence - Bose-Einstein Condensate[3]
Experimental Setup
The first experimental evidence in support of the BHM was observed in 2002.[3]
Greiner and collaborators created a Bose-Einstein condensate that was spherically symmetric, and magnetically trapped. To form the three dimensional lattice potential three optical standing waves were set up perpendicular to eachother with the crossing point of the three beams positioned at the center of the condensate. The magnetically trapped condensate was then transferred to the optical lattice by slowly increasing the beam intensity. By increasing slowly it was ensured that the atoms stayed in the many body ground state. When the beams reached full intensity the condensate was spread over more than 150,000 lattice sites with an average of 2.5 atoms per lattice cite in the center of the condenstate
Adjusting the potential depth via frequency variations allowed for Greiner et al. to essentially set the phase of the condensate. When they would set a potential, they would then turn it off. The atomic wavefunctions then expand freely and interfere with eachother. This allowed for a test of phase coherence of the system via diffraction patterns.
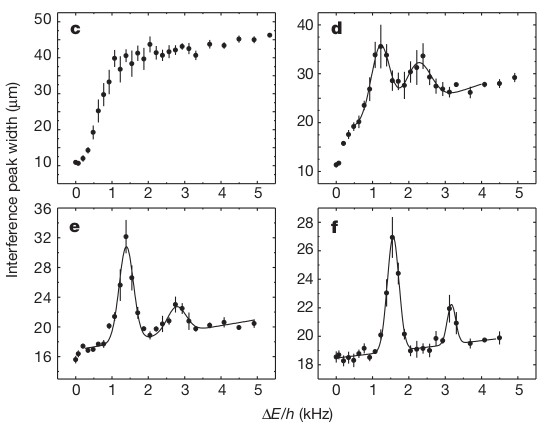
The phase was also tested by measuring the excitation spectrum of the condensate, as the superfluid state and the Mott insulator state should have markedly different spectrum's. In the Mott insulator phase the atoms are well localized in the lattice. An excitation occurs when a particle hole pair is created. For example if we had exactly one particle per lattice site, then an excitation would be when one particle tunnels to an adjacent site, creating a site with no particles and a site with two. To realize this excitation in the lab the lattice potential is tilted by the application of a potential gradient. This creates an energy difference between neighboring lattice sites that allows for the tunneling to an excited state. It was expected to see resonant excitations in the plot of intereference peak width versus energy difference in neighboring lattice sites.
Superfluid Phase
For the superfluid phase it was expected to observe sharp diffraction patterns. This is due to the fact that in the superfluid phase all atoms are delocalized, with equal relative phases between different lattice sites. Therefore the sharp diffraction patterns represent extreme phase coherence in the system.
In the excitation spectrum it was expected to not see resonant structure for the superfluid phase. It can be seen in figure 6 that this is the case. In box c, which corresponds to the superfluid lattice depth, there is no structure in the excitation spectrum
Mott Insulator Phase
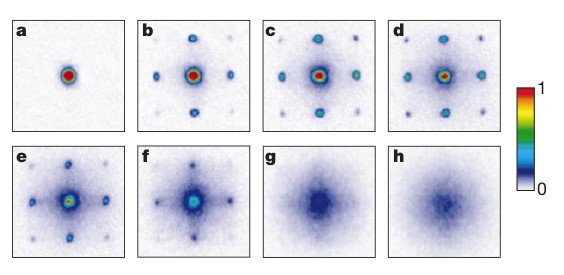
For the Mott insulator phase it was expected to have a blurred diffraction pattern. This is because the system should lose all phase coherence which will result in no observable diffraction pattern. It can be observed in figure 5 that there is a clear loss of sharp diffraction patterns in box g, this corresponds to the onset of the Mott insulator phase.
In contrast to the superfluid phase, the Mott insulator phase should display resonant features in the excitation spectrum. We can see from figure 6 that the emergence of this behavior begins in plot d. As the lattice potential depth is increased, and it transitions past the critical point where the phase transition occurs, the resonance structure becomes more clearly defined.
References
- ↑ Jump up to: 1.0 1.1 M.P.A. Fisher, P.B. Weichman, G. Grinstein, D.S. Fisher, Phys. Rev. B.40,546 (1989)
- ↑ S. Sachdev, Quantum Phase Transitions. 2nd Edition (2011)
- ↑ Jump up to: 3.0 3.1 3.2 3.3 M. Greiner, O. Mandel, T. Esslinger, T. W. Hansh, I. Bloch, Nature 415,39 (2002)