Phy5645/doubledelta: Difference between revisions

From PhyWiki
Jump to navigation Jump to search
(Double Delta potential ground state problem)
 
No edit summary
 
(5 intermediate revisions by the same user not shown)
Line 1: Line 1:
Question) Consider the potential V(x) = -g (x-a) –g (x+a),
The potential that we are considering is even, and thus the wave functions must have definite parity. We divide the one-dimensional space into three regions; region I is <math>x<-a\!</math>, region II is <math>-a<x<a\!</math>, and region III is <math>x>a.\!</math> Since the wave function must have definite parity, there are two possibilities for the form of the wave function. Let us first consider an even wave function, which will have the form,
Prove that the ground state always exists and has even parity. By means of a sketch, also show
that the first excited state exists for well separated values of 2a.


<math>\psi_I(x)=Ae^{kx},\!</math>


Ans : The potential is not affected by inversion. This implies that the wave functions have definite parity. The above potential is an attractive one. An attractive potential always has a ground state. The 1D space is divided into 3 regions. If we consider a particle with E<0, then in the leftmost and rightmost regions the wave function is of the type <math>Ae^{\left | -x \right |}</math> and <math>De^{\left | -x \right |}</math> respectively. The solution in the second region is <math>Be^{-\alpha x}+Ce^{\alpha x}</math>.
<math>\psi_{II}(x)=B\cosh{kx},\!</math>
For functions of even parity A=D, B=C. By continuity of wavefunction Ae^{-\alpha a}=Be^{-\alpha a}+Ce^{-\alpha a}. Integrating the Schrodinger equation from – ε to + ε and where ε tending to zero,


    <math>{\psi }'\left ( a+ \right )-{\psi }'\left ( a- \right )=\frac{-2mg}{\hbar^{2}}\psi \left ( a \right )</math>
<math>\psi_{III}(x)=Ae^{-kx},\!</math>
Therefore,
                <math>\alpha e^{2\alpha a}=\frac{mg}{\hbar^{2}}\left ( e^{2\alpha a}+1 \right )</math>
For function of odd parity, A= -D and B= -C. Using the same method as we followed above,we get
                <math>\alpha e^{2\alpha a}=\frac{mg}{\hbar^{2}}\left ( e^{2\alpha a}-1 \right )</math>


The first equation always has a solution whereas the second does not always have one. This is seen easily from the fact that for positive values of α, the right hand side of the second equation is zero only at the origin and increases slower than the left hand side (except if the coefficient is adjusted so that it increases faster in the beginning).
where <math>k=\frac{\sqrt{-2mE}}{\hbar}.</math>  We now apply the boundary conditions at <math>x=\pm a.\!</math> The continuity condition at <math>x=-a\!</math> gives us


[[Image:Assignment_3-_04026017.pdf_-_Adobe_Reader.png]]
<math>Ae^{-ka}=B\cosh{ka}.\!</math>


Blue: <math>xe^{x}</math>
The derivative, on the other hand, is discontinuous; the condition in it is
Red: <math>e^{x}-1</math>


[[Image:22.png]]
<math>\psi'_{II}(-a)-\psi'_I(-a)=-\frac{2mg}{\hbar^2}\psi(-a).</math>


The blue is as before. The red curve corresponds to <math>1.5\left ( e^{x}-1 \right )</math>.
This condition yields
On the other hand, for the first equation, when <math>\alpha =0</math> , the right hand side is non-zero whereas the
left hand side is zero. Yet, the right hand side increases slower. Therefore it shall be equal to the
left hand side inevitably. Hence the state that always exists corresponds to the solution of the first
equation. Hence that is the ground state.


[[Image:33.png]]
<math>-kB\sinh{ka}-kAe^{-ka}=-\frac{2mg}{\hbar^2}B\cosh{ka}.</math>


The blue curve is <math>xe^{x}</math>. The red curve is <math>e^{x}-1</math>.
The corresponding conditions at <math>x=a\!</math> yield the same equations.  We can eliminate <math>A\!</math> and <math>B\!</math> from the above equations, obtaining the following equation for <math>k\!</math>:
Therefore the ground state has even parity. If the value of the separation is large enough (so that
 
the right hand side increases faster than the left hand side), then the odd parity solution exists.
<math>(\kappa-\gamma)e^{2(\kappa-\gamma)}=\gamma e^{-2\gamma},\!</math>
Therefore the first excited state exists for large enough values of 2a.
 
where <math>\kappa=ka\!</math> and <math>\gamma=\frac{ma}{\hbar^2}g.</math>  In order for a bound state to exist, there must be a solution to the above equation for which <math>\kappa>0.\!</math>  We note that the right-hand side is always positive, while the left-hand side is only positive for <math>\kappa>\gamma\!</math> and increases indefinitely as we increase <math>\kappa.\!</math>  Therefore, there will always be a physically relevant solution of the above equation, and therefore there is always a bound state of even parity.
 
Now let us consider an odd wave function.  Such a wave function will have the form,
 
<math>\psi_I(x)=Ae^{kx},\!</math>
 
<math>\psi_{II}(x)=B\sinh{kx},\!</math>
 
<math>\psi_{III}(x)=-Ae^{-kx}.\!</math>
 
The same procedure as before yields the following equation:
 
<math>(\kappa-\gamma)e^{2(\kappa-\gamma)}=-\gamma e^{-2\gamma}.\!</math>
 
Unlike the even parity case, however, this equation may not have a solution for which <math>\kappa>0.\!</math>  First, let us note that <math>\kappa=0\!</math> is always a solution to the above equation.  If we find the minimum of the left-hand side, we find that it occurs at <math>\kappa=\gamma-\tfrac{1}{2},</math> at which point the left-hand side becomes <math>-\frac{1}{2e}.</math>  This is also the smallest value that the right-hand side can possibly take, which it acquires for <math>\gamma=\tfrac{1}{2}.</math>  If <math>\gamma\leq\tfrac{1}{2},</math> then this implies that no solution exists for which <math>\kappa>0,\!</math> since the left-hand side only becomes less than the right-hand side for negative values of <math>\kappa.\!</math>  On the other hand, if <math>\gamma>\tfrac{1}{2},</math> then we will find a solution for which <math>\kappa>0.\!</math>  Thus, a second bound state of odd parity will also exist provided that <math>\frac{2ma}{\hbar^2}g>1;</math> i.e., if the separation of the delta function wells is sufficiently large, or if their strength is sufficiently high.
 
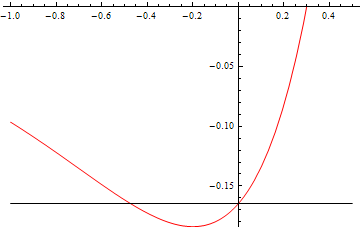
To illustrate this graphically, let us plot the left-hand side as a function of <math>\kappa\!</math> versus the right-hand side for several values of <math>\gamma\!</math>.  In all of the below plots, the red curve is the left-hand side, while the black line is the right-hand side.  Below is a plot for <math>\gamma=0.3:\!</math>
 
[[File:DoubleDelta_gamma_too_small.png]]
 
Here, we see that, in addition to <math>\kappa=0,\!</math> the only other solution is for a <math>\kappa<0,\!</math> which is unphysical.
 
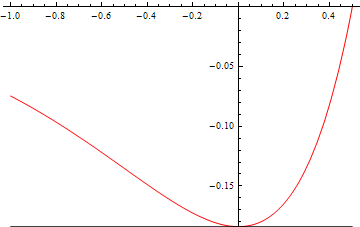
Let us now increase <math>\gamma\!</math> to <math>0.5:\!</math>
 
[[File:DoubleDelta_gamma_critical.png]]
 
The negative <math>\kappa\!</math> solution has disappeared, and we are left with the (still unphysical) trivial solution, <math>\kappa=0.\!</math>
 
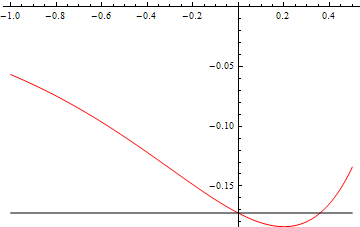
Now let us look at the plot for <math>\gamma=0.7:\!</math>
 
[[File:DoubleDelta_gamma_large_enough.png]]
 
We see that there is now a solution for which <math>\kappa>0.\!</math>
 
Back to [[The Dirac Delta Function Potential#Problem|The Dirac Delta Function Potential]]

Latest revision as of 13:30, 18 January 2014

The potential that we are considering is even, and thus the wave functions must have definite parity. We divide the one-dimensional space into three regions; region I is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x<-a\!} , region II is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -a<x<a\!} , and region III is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x>a.\!} Since the wave function must have definite parity, there are two possibilities for the form of the wave function. Let us first consider an even wave function, which will have the form,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi_I(x)=Ae^{kx},\!}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi_{II}(x)=B\cosh{kx},\!}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi_{III}(x)=Ae^{-kx},\!}

where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k=\frac{\sqrt{-2mE}}{\hbar}.} We now apply the boundary conditions at Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x=\pm a.\!} The continuity condition at Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x=-a\!} gives us

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Ae^{-ka}=B\cosh{ka}.\!}

The derivative, on the other hand, is discontinuous; the condition in it is

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi'_{II}(-a)-\psi'_I(-a)=-\frac{2mg}{\hbar^2}\psi(-a).}

This condition yields

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -kB\sinh{ka}-kAe^{-ka}=-\frac{2mg}{\hbar^2}B\cosh{ka}.}

The corresponding conditions at Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x=a\!} yield the same equations. We can eliminate Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A\!} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B\!} from the above equations, obtaining the following equation for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k\!} :

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (\kappa-\gamma)e^{2(\kappa-\gamma)}=\gamma e^{-2\gamma},\!}

where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \kappa=ka\!} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \gamma=\frac{ma}{\hbar^2}g.} In order for a bound state to exist, there must be a solution to the above equation for which Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \kappa>0.\!} We note that the right-hand side is always positive, while the left-hand side is only positive for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \kappa>\gamma\!} and increases indefinitely as we increase Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \kappa.\!} Therefore, there will always be a physically relevant solution of the above equation, and therefore there is always a bound state of even parity.

Now let us consider an odd wave function. Such a wave function will have the form,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi_I(x)=Ae^{kx},\!}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi_{II}(x)=B\sinh{kx},\!}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi_{III}(x)=-Ae^{-kx}.\!}

The same procedure as before yields the following equation:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (\kappa-\gamma)e^{2(\kappa-\gamma)}=-\gamma e^{-2\gamma}.\!}

Unlike the even parity case, however, this equation may not have a solution for which Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \kappa>0.\!} First, let us note that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \kappa=0\!} is always a solution to the above equation. If we find the minimum of the left-hand side, we find that it occurs at Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \kappa=\gamma-\tfrac{1}{2},} at which point the left-hand side becomes Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -\frac{1}{2e}.} This is also the smallest value that the right-hand side can possibly take, which it acquires for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \gamma=\tfrac{1}{2}.} If Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \gamma\leq\tfrac{1}{2},} then this implies that no solution exists for which Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \kappa>0,\!} since the left-hand side only becomes less than the right-hand side for negative values of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \kappa.\!} On the other hand, if Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \gamma>\tfrac{1}{2},} then we will find a solution for which Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \kappa>0.\!} Thus, a second bound state of odd parity will also exist provided that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{2ma}{\hbar^2}g>1;} i.e., if the separation of the delta function wells is sufficiently large, or if their strength is sufficiently high.

To illustrate this graphically, let us plot the left-hand side as a function of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \kappa\!} versus the right-hand side for several values of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \gamma\!} . In all of the below plots, the red curve is the left-hand side, while the black line is the right-hand side. Below is a plot for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \gamma=0.3:\!}

DoubleDelta gamma too small.png

Here, we see that, in addition to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \kappa=0,\!} the only other solution is for a Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \kappa<0,\!} which is unphysical.

Let us now increase Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \gamma\!} to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0.5:\!}

DoubleDelta gamma critical.png

The negative Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \kappa\!} solution has disappeared, and we are left with the (still unphysical) trivial solution, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \kappa=0.\!}

Now let us look at the plot for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \gamma=0.7:\!}

DoubleDelta gamma large enough.png

We see that there is now a solution for which Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \kappa>0.\!}

Back to The Dirac Delta Function Potential

Retrieved from "http://wiki.physics.fsu.edu/index.php?title=Phy5645/doubledelta&oldid=15793"