Solution to Set 1: Difference between revisions
ShawnHavery (talk | contribs) m (→Part c: minor repair) |
ShawnHavery (talk | contribs) (→Part a: Streamlined derivation) |
||
| (10 intermediate revisions by 2 users not shown) | |||
| Line 119: | Line 119: | ||
The de Broglie wavelength of a particle can be written as: | The de Broglie wavelength of a particle can be written as: | ||
<math> \lambda = \frac{h}{p} </math> | :<math> \lambda = \frac{h}{p} </math> | ||
The momentum can be rewritten as: | The momentum can be rewritten as: | ||
<math>\mathbf{p}= m \mathbf{v}\,\! </math> | :<math>\mathbf{p}= m \mathbf{v}\,\! </math> | ||
with ''m'' being the rest mass and ''v'' being the velocity. | with ''m'' being the rest mass and ''v'' being the velocity. | ||
| Line 131: | Line 131: | ||
The first equation is: | The first equation is: | ||
<math>\,\! E_k= |qV|</math><br> | :<math>\,\! E_k= |qV|</math><br> | ||
with ''q'' being the charge and ''V'' being the potential difference. The next equation is: | with ''q'' being the charge and ''V'' being the potential difference. The next equation is: | ||
<math> E_k = \begin{matrix} \frac{1}{2} \end{matrix} mv^2 </math> | :<math> E_k = \begin{matrix} \frac{1}{2} \end{matrix} mv^2 </math> | ||
Thus, we end up with | Thus, we end up with: | ||
<math>\,\! E_k= \begin{matrix} \frac{1}{2} \end{matrix} mv^2=|qV| </math><br> | :<math>\,\! E_k= \begin{matrix} \frac{1}{2} \end{matrix} mv^2=|qV| </math><br> | ||
Next, we must use a little algebra in order to match our previous equation of p | Next, we must use a little algebra in order to match our previous equation of p: | ||
<math>\,\! \begin{matrix} \frac{1}{2} \end{matrix} mv^2=|qV| </math><br> | :<math>\,\! \begin{matrix} \frac{1}{2} \end{matrix} mv^2=|qV| </math><br> | ||
<math>\,\! (mv)^2=2m|qV| </math><br> | :<math>\,\! (mv)^2=2m|qV| </math><br> | ||
<math>\,\! p=mv=\sqrt{2m|qV|} </math><br> | :<math>\,\! p=mv=\sqrt{2m|qV|} </math><br> | ||
Just sub this into the earlier equation for the de Broglie wavelength and you obtain: | Just sub this into the earlier equation for the de Broglie wavelength and you obtain: | ||
<math>\,\! \lambda = \frac{h}{\sqrt{2m|qV|}} </math><br> | :<math>\,\! \lambda = \frac{h}{\sqrt{2m|qV|}} </math><br> | ||
To get an expression for the de Broglie wavelength (in nanometers) of an electron in terms of the potential difference V (in volts) through which it has been accelerated, we need to identify some constants | To get an expression for the de Broglie wavelength (in nanometers) of an electron in terms of the potential difference V (in volts) through which it has been accelerated, we need to identify some constants: | ||
m<sub>e</sub> = 9. | :m<sub>e</sub> = 9.10938188×10<sup>-31</sup> kg | ||
q = 1. | :q = 1.6022×10<sup>-19</sup> C | ||
h = 6.626×10<sup>34</sup> kg m<sup>2</sup> s<sup>-1</sup> | :h = 6.626×10<sup>34</sup> kg m<sup>2</sup> s<sup>-1</sup> | ||
1 V = 1 kg m<sup>2</sup> s<sup>-2</sup> C<sup>-1</sup> | :1 V = 1 kg m<sup>2</sup> s<sup>-2</sup> C<sup>-1</sup> | ||
Therefore, | Therefore, | ||
<math>\,\! \lambda_e = \frac{1. | :<math>\,\! \lambda_e = \frac{1.226426 \ \mathrm{nm}}{\sqrt{|V/1 \mathrm{V}|}} </math><br> | ||
===Part b=== | ===Part b=== | ||
<math>\,\! \lambda_e = \frac{1. | :<math>\,\! \lambda_e = \frac{1.226426 \ \mathrm{nm}}{\sqrt{|3.0 \times 10^4 \ \mathrm{V}/1 \mathrm{V}|}} </math><br> | ||
<math>\,\! \lambda_e = 7. | :<math>\,\! \lambda_e = 7.1 \times 10^{-3} \ \mathrm{nm} </math><br> | ||
===Part c=== | ===Part c=== | ||
<math> \lambda = \frac{h}{mv} </math> | :<math> \lambda = \frac{h}{mv} </math> | ||
For this calculation, average values for walking speed (2 m/s) and mass (75 kg) will be used | For this calculation, average values for walking speed (2 m/s) and mass (75 kg) will be used: | ||
<math> \lambda = \frac{6. | :<math> \lambda = \frac{6.626 \times 10^{-34} \ \mathrm{kg \ m}^2 \ \mathrm{s}^{-1}}{(75 \ \mathrm{kg})(2 \ \mathrm{m \ s}^{-1})} = 4.4 \times 10^{-27} \ \mathrm{nm} </math> | ||
This wavelength is extremely short, suggesting that there is very little wavelike motion when the average person is walking. | This wavelength is extremely short, suggesting that there is very little wavelike motion when the average person is walking. | ||
==Problem 3== | ==Problem 3== | ||
We are told that the interaction energy <math>E</math> between two atoms as a function of their internuclear distance <math>R</math> is given by: | |||
:<math>\,\! E(R) = -\frac{A}{R^2} + \frac{B}{R^{10}} </math><br> | |||
where <math>A</math> and <math>B</math> are constants. We are also told that the atoms form a stable molecule with an internuclear distance of 0.3 nm and a dissociation energy of 4 eV. | |||
===Part a=== | ===Part a=== | ||
<math> | We are given values for <math>E</math> and <math>R</math>, but are still left with two unknowns. In order to solve for the constants <math>A</math> and <math>B</math>, another equation must be obtained. Because the molecule is stable, the interaction energy is at a minimum, and thus we may obtain a second equation by taking ''dE/dR'' and setting it equal to zero: | ||
:<math>\,\! 0 = \frac{dE}{dR} = \frac{2A}{R^3} - \frac{10B}{R^{11}} </math><br> | |||
<math> | Along with the original expression for <math>E(R)</math>, we now have a system of two equations with two unknowns. We first solve for <math>B</math> in terms of <math>A</math>: | ||
:<math>\,\! \frac{10B}{R^{11}} = \frac{2A}{R^3}</math><br> | |||
<math>\,\! B= \frac{R^8}{5} | :<math>\,\! B= \frac{R^8}{5} A </math><br> | ||
By plugging | By plugging this expression for <math>B</math> into the original equation, as well as substituting in all the values given in the problem (<math>R</math> = 0.3 nm, <math>E</math> = -4 eV), we obtain the value of <math>A</math>: | ||
<math>\,\! | :<math>\,\! E(R) = -\frac{A}{R^2} + \frac{\frac{R^8}{5}A}{R^{10}} = -\frac{A}{R^2} + \frac{A}{5R^2} = -\frac{4A}{5R^2} </math><br> | ||
<math>\,\! - | :<math>\,\! -4 \ \mathrm{eV} = -\frac{4A}{5 \ (0.3 \ \mathrm{nm})^2} = -(8.8889 \ \mathrm{nm}^{-2}) \ A </math><br> | ||
<math>\,\! A=. | :<math>\,\! A=0.45 \ \mathrm{nm}^2 \ \mathrm{eV} </math><br> | ||
We now plug the value for <math>A</math> back into the equation for <math>B</math> to find its value: | |||
<math>\,\! B=1. | :<math>\,\! B=1.312 \times 10^{-5} \ \mathrm{nm}^8 \ (0.45 \ \mathrm{nm}^2 \ \mathrm{eV}) </math><br> | ||
:<math>\,\! B=5.9049 \times 10^{-6} \ \mathrm{nm}^{10} \ \mathrm{eV} </math><br> | |||
===Part b=== | ===Part b=== | ||
To calculate the force required to break the molecule apart, we must first find the internuclear distance where the slope of the potential energy curve is steepest. This will be where the maximum attractive force is experienced between the two atoms, and so this is the force we must apply in order to separate them. | |||
We first take the negative derivative of the energy to obtain an expression for the force: | |||
:<math>\,\! F(R) = -\frac{dE}{dR} = -\frac{2A}{R^3} + \frac{10B}{R^{11}} </math><br> | |||
We then take the derivative of the force and set it equal to zero to solve for the critical internuclear distance <math>R_c</math> where the force is at a maximum: | |||
:<math>\,\! 0 = \frac{dF}{dR}\bigg|_{R = R_c} = \frac{6A}{R_c^4} - \frac{110B}{R_c^{12}} </math><br> | |||
:<math>\,\! \frac{6A}{R_c^4} = \frac{110B}{R_c^{12}} </math><br> | |||
:<math>\,\! R_c = \left(\frac{55B}{3A}\right)^\frac{1}{8} </math><br> | |||
:<math>\,\! R_c = \left(\frac{55 \ (5.9049 \times 10^{-6} \ \mathrm{nm}^{10} \ \mathrm{eV})}{3 \ (0.45 \ \mathrm{nm}^2 \ \mathrm{eV})}\right)^\frac{1}{8} </math><br> | |||
:<math>\,\! R_c = 0.3529 \ \mathrm{nm} </math><br> | |||
To obtain the separation force <math>F_s</math> required to break the molecule apart, we plug the value of <math>R_c</math> into the previous expression for the force: | |||
:<math>\,\! F_s = F(R_c) = -\frac{2 \ (0.45 \ \mathrm{nm}^2 \ \mathrm{eV})}{(0.3529 \ \mathrm{nm})^3} + \frac{10 \ (5.9049 \times 10^{-6} \ \mathrm{nm}^{10} \ \mathrm{eV})}{(0.3529 \ \mathrm{nm})^{11}} </math><br> | |||
:<math>\,\! F_s = -14.89 \ \mathrm{eV} \ \mathrm{nm}^{-1} = -2.386 \ \mathrm{nN}</math><br> | |||
==Problem 4== | ==Problem 4== | ||
The simplest of all atomic systems, the hydrogen atom consists of one proton and one electron. It is the first of a class of atomic systems that contain only one electron. The energy levels <math>E_n</math> of such a system are given by: | The simplest of all atomic systems, the hydrogen atom consists of one proton and one electron. It is the first of a class of atomic systems that contain only one electron. The energy levels <math>E_n</math> of such a system are given by: | ||
| Line 223: | Line 254: | ||
:<math>E_{r\rarr\infty} = 2E_1 = 2(-13.6 \ \mathrm{eV}) = -27.2 \ \mathrm{eV}</math> | :<math>E_{r\rarr\infty} = 2E_1 = 2(-13.6 \ \mathrm{eV}) = -27.2 \ \mathrm{eV}</math> | ||
Now let's see what happens as we bring the two atoms together, in an attempt to form a hydrogen ''molecule'': H<sub>2</sub>. | |||
===Part a=== | |||
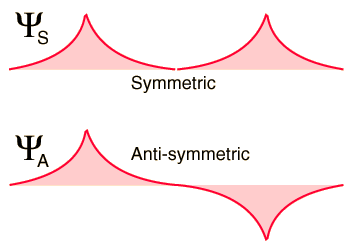
According to quantum mechanics, the spatial wavefunction for the system can be either symmetric (denoted <math>\Psi_S</math>) or antisymmetric (<math>\Psi_A</math>) about the midpoint between the atoms: | According to quantum mechanics, the spatial wavefunction for the system can be either symmetric (denoted <math>\Psi_S</math>) or antisymmetric (<math>\Psi_A</math>) about the midpoint between the atoms: | ||
[[Image:Bondwf1.gif]] | :[[Image:Bondwf1.gif]] | ||
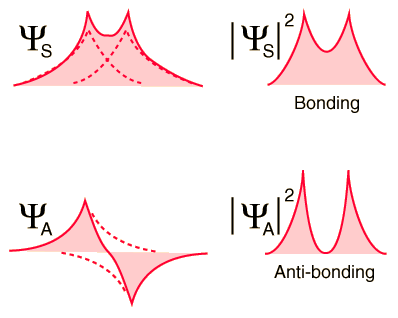
If the atoms are far apart, either of these two possibilities results in exactly the same total energy for the system (-27.2 eV). However, as the two atoms are brought closer together, each atom's contribution to the total wavefunction will either add constructively (in the case of <math>\Psi_S</math>) or destructively (in the case of <math>\Psi_A</math>), resulting in two substantially different outcomes: | If the atoms are far apart, either of these two possibilities results in exactly the same total energy for the system (-27.2 eV). However, as the two atoms are brought closer together, each atom's contribution to the total wavefunction will either add constructively (in the case of <math>\Psi_S</math>) or destructively (in the case of <math>\Psi_A</math>), resulting in two substantially different outcomes: | ||
[[Image:Bondwf2.gif]] | :[[Image:Bondwf2.gif]] | ||
As the above diagram shows, the constructive interference between the two atom's wavefunctions in the symmetric case of <math>\Psi_S</math> result in a non-zero value of the wavefunction at the midpoint between the two atoms, and thus the electron probability density <math>|\Psi_S|^2</math> between the two protons in the symmetric case is also non-zero. Thus the electrons exist between the two protons, interposing their negative charge between the repulsive positive charges of the protons and so holding the molecule together. This electronic state is stable, and is known as the ''bonding orbital''. | As the above diagram shows, the constructive interference between the two atom's wavefunctions in the symmetric case of <math>\Psi_S</math> result in a non-zero value of the wavefunction at the midpoint between the two atoms, and thus the electron probability density <math>|\Psi_S|^2</math> between the two protons in the symmetric case is also non-zero. Thus the electrons exist between the two protons, interposing their negative charge between the repulsive positive charges of the protons and so holding the molecule together. This electronic state is stable, and is known as the ''bonding orbital''. | ||
| Line 240: | Line 274: | ||
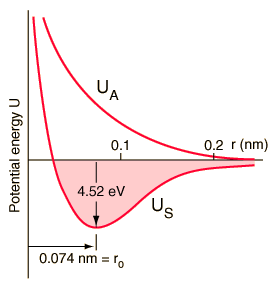
A graph of the total potential energies <math>U</math> of the bonding and antibonding orbitals of the H<sub>2</sub> system as a function of internuclear distance <math>r</math> is shown below: | A graph of the total potential energies <math>U</math> of the bonding and antibonding orbitals of the H<sub>2</sub> system as a function of internuclear distance <math>r</math> is shown below: | ||
[[Image:H2mol.gif]] | :[[Image:H2mol.gif]] | ||
For the antisymmetric case of the antibonding orbital <math>\Psi_A</math>, because the electron density is low between the two protons, the system's total potential energy <math>U_A</math> is always greater than that of two separate hydrogen atoms, and increases as the nuclei are brought together. There is no stable configuration, and indeed the energy minimum of the system is realized when the two atoms are infinitely far apart, i.e. when they are indeed two separate atoms. A molecule does not form. | For the antisymmetric case of the antibonding orbital <math>\Psi_A</math>, because the electron density is low between the two protons, the system's total potential energy <math>U_A</math> is always greater than that of two separate hydrogen atoms, and increases as the nuclei are brought together. There is no stable configuration, and indeed the energy minimum of the system is realized when the two atoms are infinitely far apart, i.e. when they are indeed two separate atoms. A molecule does not form. | ||
Latest revision as of 00:20, 6 February 2009
Problem 1
Part a
It is a common misconception that Max Planck derived his now-famous law, Planck's Law, in order to resolve the so-called "ultraviolet catastrophe," which predicts, from classical physics, that a blackbody will emit greater and greater intensity radiation at shorter wavelengths, thus outputting infinite power as electromagnetic radiation. In fact, this problem was not noticed until five years after Planck derived his law.
What actually motivated Planck was his desire to improve on the Wien approximation, which fit known blackbody radiation spectra only at short wavelengths. Expressed as spectral radiance:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I(\lambda, T) = \frac{2 h c^2} {\lambda^5} e^{-\frac{hc}{\lambda kT}}}
Conversely, the Rayleigh-Jeans law fit the data only at long wavelengths:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I(\lambda, T) = \frac{2 c k T}{\lambda^4}}
Planck derived his function to fit the data at all wavelengths:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I(\lambda,T) =\frac{2 hc^2}{\lambda^5}\frac{1}{ e^{\frac{hc}{\lambda kT}}-1}}
Planck derived his law via a consideration of various ways in which electromagnetic energy can be distributed over the different modes of oscillation of charged oscillators in matter (today known to be atoms). He found that when he assumed the energy to be quantized, the above law emerged and fit the data very well.
Part b
Planck's law, expressed as spectral radiance in terms of wavelength and temperature:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I(\lambda,T) =\frac{2hc^2}{\lambda^5}\frac{1}{e^{\frac{hc}{\lambda kT}}-1}}
From the above, we will derive Wien's displacement law:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda_{\mathrm{max}} = \frac{b}{T}}
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda_{\mathrm{max}}} is the wavelength of maximum intensity electromagnetic radiation output for a blackbody in thermal equilibrium at absolute temperature Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T} , and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b} is a proportionality constant (for our purposes here, it will not be necessary to calculate the exact value of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b} , only to show that it must be a constant).
Differentiating Planck's law with respect to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda} :
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{dI}{d\lambda} = 2hc^2\left(-\frac{5}{\lambda^6}\frac{1}{e^{\frac{hc}{\lambda kT}}-1} + \frac{1}{\lambda^5}\frac{hc}{kT}\frac{1}{\lambda^2}\frac{e^{\frac{hc}{\lambda kT}}}{(e^{\frac{hc}{\lambda kT}}-1)^2}\right) = 2hc^2\left(-\frac{5}{\lambda^6}\frac{1}{e^{\frac{hc}{\lambda kT}}-1} + \frac{hc}{\lambda^7 kT}\frac{e^{\frac{hc}{\lambda kT}}}{(e^{\frac{hc}{\lambda kT}}-1)^2}\right)}
To find Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda_{\mathrm{max}}} , we set Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{dI}{d\lambda} = 0} and solve:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2hc^2\left(-\frac{5}{\lambda_{\mathrm{max}}^6}\frac{1}{e^{\frac{hc}{\lambda_{\mathrm{max}} kT}}-1} + \frac{hc}{\lambda_{\mathrm{max}}^7 kT}\frac{e^{\frac{hc}{\lambda_{\mathrm{max}} kT}}}{(e^{\frac{hc}{\lambda_{\mathrm{max}} kT}}-1)^2}\right) = 0}
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -\frac{5}{\lambda_{\mathrm{max}}^6}\frac{1}{e^{\frac{hc}{\lambda_{\mathrm{max}} kT}}-1} + \frac{hc}{\lambda_{\mathrm{max}}^7 kT}\frac{e^{\frac{hc}{\lambda_{\mathrm{max}} kT}}}{(e^{\frac{hc}{\lambda_{\mathrm{max}} kT}}-1)^2} = 0}
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{hc}{\lambda_{\mathrm{max}}^7 kT}\frac{e^{\frac{hc}{\lambda_{\mathrm{max}} kT}}}{(e^{\frac{hc}{\lambda_{\mathrm{max}} kT}}-1)^2} = \frac{5}{\lambda_{\mathrm{max}}^6}\frac{1}{e^{\frac{hc}{\lambda_{\mathrm{max}} kT}}-1}}
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{hc}{\lambda_{\mathrm{max}} kT}\frac{e^{\frac{hc}{\lambda_{\mathrm{max}} kT}}}{e^{\frac{hc}{\lambda_{\mathrm{max}} kT}}-1} = 5}
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{hc}{\lambda_{\mathrm{max}} kT}\frac{1}{1-e^{-\frac{hc}{\lambda_{\mathrm{max}} kT}}} = 5}
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -\frac{5}{\lambda_{\mathrm{max}}^6}\frac{1}{e^{\frac{hc}{\lambda_{\mathrm{max}} kT}}-1} + \frac{hc}{\lambda_{\mathrm{max}}^7 kT}\frac{e^{\frac{hc}{\lambda_{\mathrm{max}} kT}}}{(e^{\frac{hc}{\lambda_{\mathrm{max}} kT}}-1)^2} = 0}
Now, for simplicity we define:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \chi \equiv \frac{hc}{\lambda_{\mathrm{max}} kT}}
and we have:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\chi}{1-e^{-\chi}} = 5}
It is clear from the above equation that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \chi} must be a constant. If Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \chi} is a constant, then examination of its definition above reveals only two non-constant terms: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T} . We thus rearrange the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \chi} equation to give a simple relation between these two variables:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda_{\mathrm{max}} = \frac{hc}{k\chi}\frac{1}{T}}
Defining a constant of proportionality Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b} :
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b \equiv \frac{hc}{k\chi}}
we now have Wien's displacement law in its most generic form:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda_{\mathrm{max}} = \frac{b}{T}}
Part c
The Stefan-Boltzmann law states that the total irradiance (total energy radiated per unit surface area per unit time), j*, emitted by a blackbody in thermal equilibrium at temperature Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T} is given as:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle j^\star = \sigma T^4}
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma} is a proportionality constant. We will now derive this relation from Planck's law, expressed as spectral radiance in terms of radiant frequency and temperature:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I(\nu,T) = \frac{2 h\nu^3}{c^2}\frac{1}{ e^{\frac{h\nu}{kT}}-1}}
In order to obtain the total irradiance of a blackbody following Planck's law, we must integrate its spectral radiance Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I} over a half-sphere of solid angle and over all frequencies:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle j^\star = \int_0^\infty{I(\nu,T) d\nu}\int_{half-sphere}{d\Omega}}
First, the solid angle:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle j^\star = \int_0^\infty{I(\nu,T) d\nu} \int_{half-sphere}{\sin\theta ~ d\theta ~ d\phi} = \int_0^\infty{I(\nu,T) d\nu} \int_0^{2\pi}{d\phi} \int_0^\frac{\pi}{2}{\cos\theta ~ \sin\theta ~ d\theta}}
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = 2\pi\int_0^\infty{I(\nu,T) d\nu} \int_0^1{\sin\theta ~ d(\sin\theta)} = \pi\int_0^\infty{I(\nu,T) d\nu}}
Now we substitute Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I(\nu,T)} from Planck's law:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle j^\star = \pi\int_0^\infty{\frac{2 h\nu^3}{c^2}\frac{1}{e^{\frac{h\nu}{kT}}-1} d\nu} = \frac{2\pi h}{c^2}\int_0^\infty{\frac{\nu^3}{e^{\frac{h\nu}{kT}}-1} d\nu}}
We now define:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \chi \equiv \frac{h\nu}{kT}}
and from this substitute the following:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \nu = \frac{kT}{h}\chi ~, ~~ d\nu = \frac{kT}{h}d\chi}
into our above expression for j*:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle j^\star = \frac{2\pi h}{c^2}\int_0^\infty{\frac{(\frac{kT}{h}\chi)^3}{e^\chi-1} \frac{kT}{h}d\chi} = \frac{2\pi k^4}{h^3 c^2}T^4\int_0^\infty{\frac{\chi^3}{e^\chi-1} d\chi} }
Using the given integral:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int_0^{\infty}[x^3 /[e^x -1] dx = \pi^4 /15}
we have:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle j^\star = \frac{2\pi^5 k^4}{15h^3 c^2}T^4}
Identifying the proportionality constant:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma \equiv \frac{2\pi^5 k^4}{15h^3 c^2}}
we now have the Stefan-Boltzmann law:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle j^\star = \sigma T^4}
Problem 2
Part a
The de Broglie wavelength of a particle can be written as:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda = \frac{h}{p} }
The momentum can be rewritten as:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{p}= m \mathbf{v}\,\! }
with m being the rest mass and v being the velocity.
In order to write the expression for de Broglie wavelength in terms of potential difference V, a relationship between p and v must be established. This can be done by equating two equations for kinetic energy.
The first equation is:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \,\! E_k= |qV|}
with q being the charge and V being the potential difference. The next equation is:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_k = \begin{matrix} \frac{1}{2} \end{matrix} mv^2 }
Thus, we end up with:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \,\! E_k= \begin{matrix} \frac{1}{2} \end{matrix} mv^2=|qV| }
Next, we must use a little algebra in order to match our previous equation of p:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \,\! \begin{matrix} \frac{1}{2} \end{matrix} mv^2=|qV| }
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \,\! (mv)^2=2m|qV| }
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \,\! p=mv=\sqrt{2m|qV|} }
Just sub this into the earlier equation for the de Broglie wavelength and you obtain:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \,\! \lambda = \frac{h}{\sqrt{2m|qV|}} }
To get an expression for the de Broglie wavelength (in nanometers) of an electron in terms of the potential difference V (in volts) through which it has been accelerated, we need to identify some constants:
- me = 9.10938188×10-31 kg
- q = 1.6022×10-19 C
- h = 6.626×1034 kg m2 s-1
- 1 V = 1 kg m2 s-2 C-1
Therefore,
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \,\! \lambda_e = \frac{1.226426 \ \mathrm{nm}}{\sqrt{|V/1 \mathrm{V}|}} }
Part b
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \,\! \lambda_e = \frac{1.226426 \ \mathrm{nm}}{\sqrt{|3.0 \times 10^4 \ \mathrm{V}/1 \mathrm{V}|}} }
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \,\! \lambda_e = 7.1 \times 10^{-3} \ \mathrm{nm} }
Part c
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda = \frac{h}{mv} }
For this calculation, average values for walking speed (2 m/s) and mass (75 kg) will be used:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda = \frac{6.626 \times 10^{-34} \ \mathrm{kg \ m}^2 \ \mathrm{s}^{-1}}{(75 \ \mathrm{kg})(2 \ \mathrm{m \ s}^{-1})} = 4.4 \times 10^{-27} \ \mathrm{nm} }
This wavelength is extremely short, suggesting that there is very little wavelike motion when the average person is walking.
Problem 3
We are told that the interaction energy Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E} between two atoms as a function of their internuclear distance Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle R} is given by:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \,\! E(R) = -\frac{A}{R^2} + \frac{B}{R^{10}} }
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B} are constants. We are also told that the atoms form a stable molecule with an internuclear distance of 0.3 nm and a dissociation energy of 4 eV.
Part a
We are given values for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle R} , but are still left with two unknowns. In order to solve for the constants Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B} , another equation must be obtained. Because the molecule is stable, the interaction energy is at a minimum, and thus we may obtain a second equation by taking dE/dR and setting it equal to zero:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \,\! 0 = \frac{dE}{dR} = \frac{2A}{R^3} - \frac{10B}{R^{11}} }
Along with the original expression for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E(R)} , we now have a system of two equations with two unknowns. We first solve for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B} in terms of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A} :
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \,\! \frac{10B}{R^{11}} = \frac{2A}{R^3}}
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \,\! B= \frac{R^8}{5} A }
By plugging this expression for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B} into the original equation, as well as substituting in all the values given in the problem (Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle R} = 0.3 nm, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E} = -4 eV), we obtain the value of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A} :
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \,\! E(R) = -\frac{A}{R^2} + \frac{\frac{R^8}{5}A}{R^{10}} = -\frac{A}{R^2} + \frac{A}{5R^2} = -\frac{4A}{5R^2} }
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \,\! -4 \ \mathrm{eV} = -\frac{4A}{5 \ (0.3 \ \mathrm{nm})^2} = -(8.8889 \ \mathrm{nm}^{-2}) \ A }
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \,\! A=0.45 \ \mathrm{nm}^2 \ \mathrm{eV} }
We now plug the value for back into the equation for to find its value:
Part b
To calculate the force required to break the molecule apart, we must first find the internuclear distance where the slope of the potential energy curve is steepest. This will be where the maximum attractive force is experienced between the two atoms, and so this is the force we must apply in order to separate them.
We first take the negative derivative of the energy to obtain an expression for the force:
We then take the derivative of the force and set it equal to zero to solve for the critical internuclear distance where the force is at a maximum:
To obtain the separation force required to break the molecule apart, we plug the value of into the previous expression for the force:
Problem 4
The simplest of all atomic systems, the hydrogen atom consists of one proton and one electron. It is the first of a class of atomic systems that contain only one electron. The energy levels of such a system are given by:
where is the number of protons in the nucleus (the nuclear charge, or the atom's atomic number) and is the ground state energy of the hydrogen atom. The latter may be calculated via the Bohr model of the atom:
where and are, respectively, the mass and charge of the electron, is Planck's constant, and is the vacuum permittivity.
If we place two hydrogen atoms far enough apart so that their interaction is negligible, the total energy of the system is just that of two hydrogen atoms:
Now let's see what happens as we bring the two atoms together, in an attempt to form a hydrogen molecule: H2.
Part a
According to quantum mechanics, the spatial wavefunction for the system can be either symmetric (denoted ) or antisymmetric () about the midpoint between the atoms:
If the atoms are far apart, either of these two possibilities results in exactly the same total energy for the system (-27.2 eV). However, as the two atoms are brought closer together, each atom's contribution to the total wavefunction will either add constructively (in the case of ) or destructively (in the case of ), resulting in two substantially different outcomes:
As the above diagram shows, the constructive interference between the two atom's wavefunctions in the symmetric case of result in a non-zero value of the wavefunction at the midpoint between the two atoms, and thus the electron probability density between the two protons in the symmetric case is also non-zero. Thus the electrons exist between the two protons, interposing their negative charge between the repulsive positive charges of the protons and so holding the molecule together. This electronic state is stable, and is known as the bonding orbital.
In contrast, the two atom's wavefunctions in the antisymmetric case of cancel out entirely at the midpoint between the atoms, resulting in an electron probability density of zero between the two protons. The electrons therefore do not exist between the two protons, and so they do little to shield their positive charges from one another. The resulting configuration is not stable, and this electronic state is known as the antibonding orbital.
It should also be noted that since the two electrons in the H2 system are identical fermions, they must obey the Paul exclusion principle; that is, the total wavefunction must be antisymmetric with respect to exchange of the two electrons. Thus, the symmetric spatial wavefunction of the bonding orbital must be paired with an antisymmetric spin wavefunction , resulting in a singlet ground state (), and the antisymmetric spatial wavefunction of the antibonding orbital must be paired with a symmetric spin wavefunction , resulting in a triplet excited state ().
Part b
A graph of the total potential energies of the bonding and antibonding orbitals of the H2 system as a function of internuclear distance is shown below:
For the antisymmetric case of the antibonding orbital , because the electron density is low between the two protons, the system's total potential energy is always greater than that of two separate hydrogen atoms, and increases as the nuclei are brought together. There is no stable configuration, and indeed the energy minimum of the system is realized when the two atoms are infinitely far apart, i.e. when they are indeed two separate atoms. A molecule does not form.
For the symmetric case of the bonding orbital , because the electron density is high between the two protons, the system's total potential energy falls as the internuclear distance decreases from infinity, eventually reaching a minimum when the two protons are at a separation distance of . This is the most stable configuration, since if the atoms are brought even closer together the potential energy begins to increase as the repulsion between the two protons begins to dominate over the shielding effect of the electrons, eventually pushing the energy higher than that of two separate hydrogen atoms. So for the symmetric case of the bonding orbital, a molecule does indeed form with maximum stability when the internuclear distance is = 0.074 nm, defining the bond length of H2, and the potential energy is at a minimum of -31.7 eV, or 4.52 eV below that of two separate hydrogen atoms.
Part c
The energy needed to break the bond in H2 (its binding energy) is simply the difference in energy between the bound and unbound states. As stated above, the total potential energy of the H2 molecule is -31.7 eV, whereas the total energy of two separate hydrogen atoms is 2(-13.6 eV) = -27.2 eV. Thus, the binding energy of the hydrogen molecule is: