4th Week: Decays, Tunneling and Cross Sections

Nuclear Radiation

Figure 1. A table of known stable and radioactive nuclides

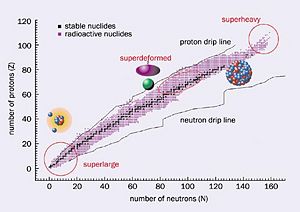
When looking at the table of nuclides it is obvious that the valley of stability is only a small percentage of all known nuclei. So most nuclei are considered unstable. To become stable these nuclides emit ionizing particles and radiation, resulting in a loss of energy from the original nuclei. This process is called radioactive decay.

Alpha Decay and Fission

Alpha decay is the transformation of a parent nucleus to a daughter nucleus through the emission of a helium nucleus. This decay is usually seen in heavier elements with too many protons. This causes excessive repulsion due to the coulomb force. In an attempt to get rid of this excessive repulsion the nucleus emits an alpha particle.

$_{Z}^{A}{\textrm {X}}\to \;_{Z-2}^{A-4}{\textrm {Y}}+\;_{2}^{4}{\textrm {He}}\ ,$

$_{Z}^{A}{\textrm {X}}\to \;\approx _{Z/2}^{A/2}{\textrm {P}}\;+\;\approx _{Z/2}^{A/2}{\textrm {Q}}\ .$

Alpha decay and nuclear fission are both considered to be a two body disintegration. In the case of an alpha decay, the daughter nucleus is at rest and most of the released energy is carried away by the alpha particle. For fission the energy is distributed between the two daughter nuclei.

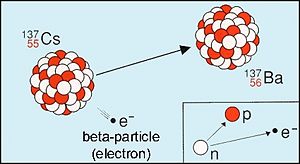
Beta Decay

Figure 2. This is two examples of the beta decay process

There are three types of beta decays, $\beta ^{-}$-decay, $\beta ^{+}$-decay, and electron capture. All three of these decays can be characterized by $\Delta A=0$ and $|\Delta Z|=1$.

The first one, $\beta ^{-}$decay, occurs when a nucleus with an over abundance of neutrons transforms to a more stable nucleus by emitting an electron. This process can be denoted as:

$_{Z}^{A}{\textrm {X}}\to \;_{Z+1}^{A}{\textrm {Y}}+\;e^{-}+{\bar {\nu _{e}}}\ .$

With,

$\;M_{n}(Z,A)>M_{n}(Z+1,A)+m_{e}$

From electric-charge conservation, the proton number in such decays is increased by one unit.

Likewise, a $\beta ^{+}$-decay occurs when a proton-rich nucleus emits a positron, therefore reducing the nuclear charge by one.

$_{Z}^{A}{\textrm {X}}\to \;_{Z-1}^{A}{\textrm {Y}}+\;e^{+}+\nu _{e}\ .$

with,

$\;M_{n}(Z,A)>M_{n}(Z-1,A)+m_{e}$

The final case, electron capture, is similar to $\beta ^{+}$-decay because it is another way for a proton-rich nucleus to reduce its nuclear charge by the capture of an electron

$_{Z}^{A}{\textrm {X}}+e^{-}\to \;_{Z-1}^{A}{\textrm {Y}}+\nu _{e}\ .$

With,

$\;M_{n}(Z,A)+m_{e}>M_{n}(Z-1,A)$

Gamma Decay

When a nucleus changes its state from the higher energetic state to the lower energetic state an electromagnetic radiation will be emitted in terms of high energy photons. This process is known as a gamma decay, and the decayed photon is called gamma-particle. In this case both the parent and daughter nuclei are the same, as the number of protons and neutrons do not change.

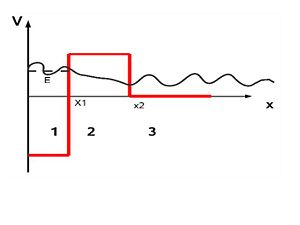
Transmission probabilities through the potential barriers

Box potential plus square well

The transmission probability in general is given by

$T={\frac {j_{fin}}{j_{in}}}\ ,$

where $j$ is quantum-mechanical flux

${\vec {j}}={\frac {\hbar }{2mi}}\left(\phi ^{*}{\vec {\nabla }}\phi -\phi {\vec {\nabla }}\phi ^{*}\right)\ .$

Using the so called WKB approximation it can be calculated through the following formula

$T\approx e^{-{\frac {2}{\hbar }}\int _{x_{1}}^{x_{2}}{\sqrt {2m(V(x)-E)}}}\ ,$

where $x_{1}$ and $x_{2}$ are turning points, $V(x)$ is the potential.This shows that a particle approaching the potential barrier from the right can reach the left side even if its energy is less than the barrier height. This is referred to as tunnel effect and is important for charged particle reactions in stars.

Coulomb barrier

This is the energy barrier due to electrostatic interaction that two nuclei need to overcome so they can get close enough to undergo nuclear fusion. This energy barrier is given by the electrostatic potential energy:

$U_{coul}=k{{q_{1}\,q_{2}} \over r}={1 \over {4\pi \epsilon _{0}}}{{q_{1}\,q_{2}} \over r}\ ,$

where k is the Coulomb's constant, and equal to k = 8.9876×10⁹ N m² C⁻², and q₁, q₂ are the charges of the interacting nuclei.

For the Coulomb potential the transition probability is calculated using the WKB approximation

$T=e^{-2\pi \eta }\ ,$

This is called Gamow factor and is important for the thermonuclear reaction rates for charged particles, where $\eta$ is the Sommerfeld parameter given by

$\eta ={\sqrt {\frac {m}{2E}}}{\frac {Z_{1}Z_{2}e^{2}}{\hbar }}\ .$

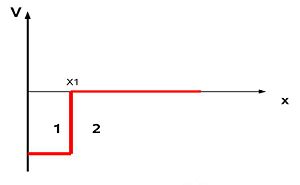
Box potential

Figure 3. The final potential well

For a finite box potential shown in Fig. 3 the transmission coefficient is easily calculated using the Schrodinger equation.

$T\approx {\frac {4k_{1}}{k_{2}}}\ ,$

where

$k={\frac {\sqrt {2m(E-V)}}{\hbar }}\ .$

Nuclear cross section

The nuclear cross section is used to characterize the probability that the nuclear reactions occur. Generally it can be written as

$\sigma ={\frac {\mbox{number of reactions per target per second}}{\mbox{flux of incoming projectiles}}}\ .$

It is related to the tunneling probability through the expression

$\sigma ={\frac {\pi }{k^{2}}}\sum _{l=0}^{\infty }(2l+1)T_{l}\ .$

To calculate the cross section one needs to know the incoming flux which is described by plane wave

$\psi _{in}=e^{i{\vec {k}}{\vec {r}}}=e^{ikr\cos \theta }={\sqrt {4\pi }}\sum _{l=0}^{\infty }{\sqrt {2l+1}}i^{l}j_{l}(kr)Y_{l,0}(\theta )\ ,$

where $j_{l}(kr)$ are spherical Bessel functions, and $Y_{l,0}$ are spherical harmonics.

We introduce the astrophysical factor S(E) which varies less with energy compared to the cross section and is given by

$\;S(E)=\sigma (E)Ee^{2\pi \eta }$

Because S(E) is not as dependent as the cross section in energy, it is a very useful concept for Nuclear astrophysicist.

Resonance reaction in a compound nucleus

In the complexity of the compound nucleus we have two different cross section approaches for the reaction $i+j\rightarrow o+m$

Statistical Model (Hauser-Feshbach). In the case where the resonances are broader and close together, the cross section varies smoothly with energy and can be approached as

$\sigma (j,o)={\pi ^{2} \over k_{j}^{2}}{(1+\delta _{ij}) \over (2I_{i}+1)(2I_{j}+1)}\sum _{j,\pi }(2J_{n}+1){T_{j}(E,j,\pi )T_{o}(E,j,\pi ) \over T_{tot}(E,j,\pi )}$

Individual resonance dominates (Breit-Wigner). When the reaction presents an isolated narrow resonances we can approximate the cross section by

$\sigma (j,k)={\pi ^{2} \over k_{j}^{2}}{(1+\delta _{ij}) \over (2I_{i}+1)(I_{j}+1)}\sum _{n}(2J_{n}+1){\Gamma _{j,n}\Gamma _{o,n} \over (E-E_{n})^{2}+(\Gamma _{n}/2)^{2}}$

Unknown chapter at this moment (please, complete)

$E_{\alpha }=E_{centerofmass}{\frac {M_{product}+M_{reaction}}{M_{reaction}}},\;\;\;\;E_{centerofmass}=E_{\alpha }{\frac {M_{reaction}}{M_{reaction}+M_{product}}}$

Example: $_{}^{56}{\textrm {Fe}}(\alpha ,2n)_{}^{58}{\textrm {Ni}}\;\;\;$ nuclear reaction with alpha particle of 20 MeV

$\alpha +_{}^{56}{\textrm {Fe}}\Rightarrow _{}^{60}{\textrm {Ni}}\Rightarrow _{}^{58}{\textrm {Ni}}+n+n$

$E_{centerofmass}=18.6MeV$