Solution to Set 5

I have no idea what I'm doing - KimberlyWynne 03:11, 2 March 2009 (EST)

Diatomic harmonic chain

Problem 1

I found this site somewhat helpful and explanatory:

http://newton.ex.ac.uk/teaching/resources/rjh/phy2009/PHY2009handout13.pdf

Given

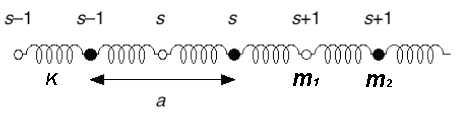
• a chain of atoms
• with alternating masses $m_{1}\;$ and $m_{2}\;$
• connected with elastic springs with constant $K\;$
• moving only in the x-direction

Derive the dispersion relation $\omega ^{\alpha }(k)\;$ for this chain

Equations of motion

$m_{1}{\ddot {u}}_{n}=-k_{1}[2u_{n}-v_{n}-v_{n-1}]\;$ $m_{2}{\ddot {v}}_{n}=-k_{2}[2v_{n}-u_{n}-u_{n+1}]\;$

$\omega ^{2}=k({\frac {m_{1}+m_{2}}{m_{1}m_{2}}})\pm k{\sqrt {({\frac {m_{1}+m_{2}}{m_{1}m_{2}}})^{2}-{\frac {4}{m_{1}m_{2}}}sin^{2}({\frac {ka}{2}})]}}\;$

Problem 2

Determine the speed of sound for this chain. What is the lowest frequency of long-wavelength sound corresponding to the optical branch?

$\omega _{\alpha }(k)\approx C_{\alpha }k\;$

where

• $\omega _{\alpha }\;$ = frequency
• $C_{\alpha }\;$ = speed of sound
• $k\;$ = ???

Problem 3

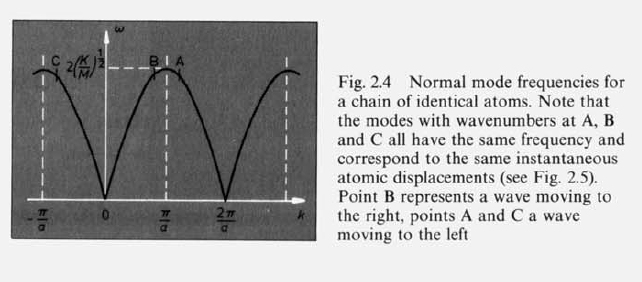
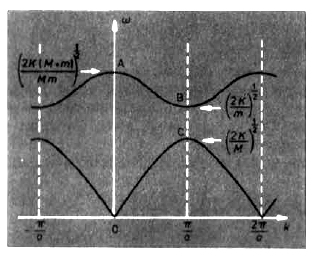
Sketch the motion of the atoms corresponding to the edge of the Brillouin zone, both for the optical and the acoustic branch.

• Acoustic Branch: lower branch
• Optical Branch: upper branch, as $k\rightarrow 0$ on this branch the vibrations of the 2 types of atom are in antiphase and the resulting charge oscillation in an ionic craystal give a strong coupling to electromagnetic waves at the frequency of point A.

Problem 4

Determine the Debye temperature for this system, and determine the form of the specific heat $C_{V}(T)$ in the limits of high and low temperatures.

Debye Temperature $T_{D}\;$

The Debye temperature, aka the effective sonic velocity, is a measure of the hardness of the crystal

From our class lectures:

$k_{B}T_{D}=\hbar \omega _{D}=\hbar ck_{D}\;$

From Wikipedia:

$T_{D}\ {\stackrel {\mathrm {def} }{=}}\ {hc_{s}R \over 2Lk}={hc_{s} \over 2Lk}{\sqrt[{3}]{6N \over \pi }}={hc_{s} \over 2k}{\sqrt[{3}]{{6 \over \pi }{N \over V}}}$

Specific Heat $C_{V}\;$

Low Temperature Limit

${\frac {C_{V}}{Nk}}\sim {12\pi ^{4} \over 5}\left({T \over T_{D}}\right)^{3}$

High Temperature Limit

$T_{high}>>{\frac {\hbar \omega }{k_{B}}}\;$

${\frac {\hbar \omega }{k_{B}T}}<<1\;$

$e^{\frac {\hbar \omega }{k_{B}T}}\approx 1+{\frac {\hbar \omega }{k_{B}T}}+({\frac {\hbar \omega }{k_{B}T}})^{2}\;$

${\frac {C_{V}}{Nk}}\sim 3\,$

Net Result (Classical Limit)

$C_{V}\approx k_{B}\;$

Problem 5

Consider low temperatures (Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T \ll T_D\;} ) and determine the wavelength of the most abundant phonons Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda_{max}}

Given

• Bose-Einstein Distribution Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(E)=\frac{1}{e^{E / k_B T}-1} \;}
  • Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(E) \;} = probability that a particle will have energy E
  • Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k_B \;} = Boltzmann constant
  • Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T \;} = Temperature

• Planck's Radiation Formula Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E = \frac{h \omega}{e^{h \omega / k_B T} - 1} \;}
  • Density by frequency: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho (\omega) = \frac{dn_s}{d\omega} = \frac{8 \pi}{c^3} \omega^{2} \;}
  • Density by wavelength: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho (\lambda) = \frac{dn_s}{d\lambda} = \frac{8 \pi}{\lambda^{4}} \;}

• Wien's law Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda_{\mathrm{max}} = \frac{b}{T} \;}
  • Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda_max \;} is the peak wavelength in meters,
  • Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T \;} = temperature of the blackbody in Kelvin
  • Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b \;} = Wien's displacement constant