7th Week: Stellar Structure and Evolution: Difference between revisions
| Line 103: | Line 103: | ||
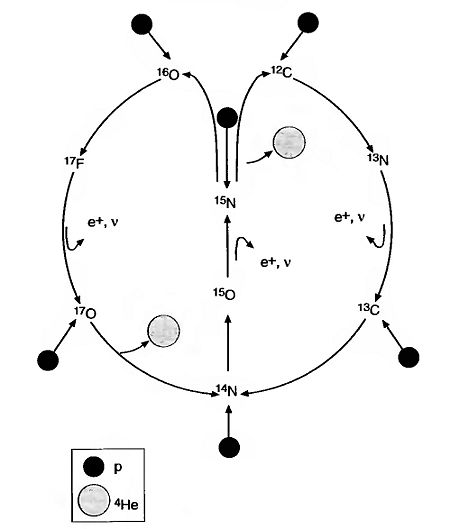
:<math>^{14}N + ^1H \rightarrow ^{15}O + \gamma \ , </math> | :<math>^{14}N + ^1H \rightarrow ^{15}O + \gamma \ , </math> | ||
:<math>^{15}O \rightarrow ^{15}N + e^+ \nu \ , </math> | :<math>^{15}O \rightarrow ^{15}N + e^+ + \nu \ , </math> | ||
:<math>^{15}N + ^1H \rightarrow ^{16}O + \gamma \ , </math> | :<math>^{15}N + ^1H \rightarrow ^{16}O + \gamma \ , </math> | ||
:<math>^{16}O + ^1H \rightarrow ^{17}F + \gamma \ , </math> | :<math>^{16}O + ^1H \rightarrow ^{17}F + \gamma \ , </math> | ||
:<math>^{17}F \rightarrow ^{17}O + e^+ + \nu \ , </math> | :<math>^{17}F \rightarrow ^{17}O + e^+ + \nu \ , </math> | ||
:<math>^{17}O + ^1H \rightarrow ^{14}N + ^4He \ . </math> | :<math>^{17}O + ^1H \rightarrow ^{14}N + ^4He \ . </math> | ||
Revision as of 18:38, 19 March 2009
As we look at the sky in the night, we can see that the Universe has a very complicated structure: planets, stars, galaxies, clusters etc. To understand how this stellar structure formed we use our knowledge of nuclear physics combined with cosmology.
Stellar properties
The Hertzsprung-Russel diagram
Stellar structure
Stars of different mass and age have varying internal structures. Stellar structure models describe the internal structure of a star in detail and make detailed predictions about the luminosity, the color and the future evolution of the star.
Equations of stellar structure
Pressure equilibrium: Pressure and gravity must balance or the star will expand or contract. The balance of the gravity force and the pressure gradient is known as the hydrostatic balance.
Conservation of mass
Energy generation: To keep the temperature constant everywhere luminosity must be generated.Considering the energy leaving the spherical shell yields the energy equation
where is the energy generation rate (sum of all energy sources and losses) per g and s
Energy transport: The temperature inside a star must increase progressively towards its center to make energy flow from the center to the surface. The energy transport equation takes differing forms depending upon the mode of energy transport.
For the case of convective luminosity transport we have
where is the adiabatic index, the ratio of specific heats in the gas
For radiative energy transport we have
where is the opacity of the matter and is the radiation density constant equal to
For conductive luminosity transport (appropriate for a white dwarf), the energy equation is
where k is the thermal conductivity.
Stellar evolution
The evolution of stars is due to their sustained emission of radiation originating from an internal source. The energy source that supplies the luminosity of stars during most of their lifetimes is nuclear fusion, which turns a small fraction of the rest mass into energy.
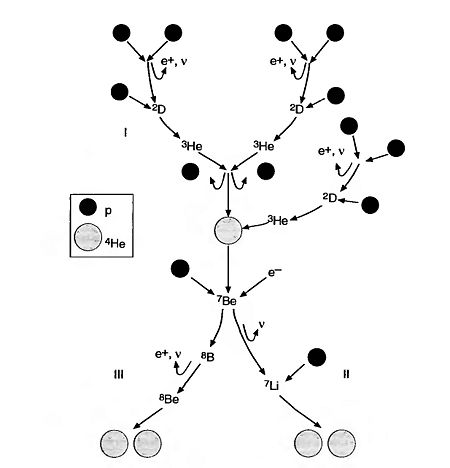
Hydrogen burning I: the p-p chain
The most abundant element in newly born stars is hydrogen. Fusion of hydrogen into the next element, helium, would require an encounter of three or four protons - hydrogen nuclei - within the distances of the order fermis (1E-15 m). The probability of such a multiple encounter is small, therefore this process does not happen at once, but gradually through the chain of reactions. The first link of this chain is the fusion of two protons
that forms a stable isotope of hydrogen. Then deuterium captures a proton to form the lighter isotope of helium
where indicates the emission of an energetic photon that soon will be absorbed by other particles. Now the reaction becomes more complicated: two nuclei form the stable isotope of helium,
and later
This is the end of the so called p-p chain I.
The p-p chain II starts with the electron capture by the beryllium nucleus
and then a subsequent capture of the proton
then ends. The p-p chain III results by capturing proton by beryllium nucleus instead of an electron capture
Since is radioactive it decays
and the since is highly unstable it goes through the reaction
Hydrogen burning II: the CNO bi-cycle
The small percentage of initial composition of stars consist of carbon, nitrogen, and oxygen nuclei. These nuclei may induce a chain of reactions that transform the hydrogen into helium. This procedure is first introduced by Bethe and is known as the CNO cycle. Since there are two such cycles, therefore we call it CNO bi-cycle.
The cycle one is as following:
And the cycle two is: