7th Week: Stellar Structure and Evolution

As we look at the sky in the night, we can see that the Universe has a very complicated structure: planets, stars, galaxies, clusters etc. To understand how this stellar structure formed we use our knowledge of nuclear physics combined with cosmology.

Stellar properties

Here we make the way to identify how stars are grouped and classified. This classification scheme identify stars by the following:

magnitudes - observational measure of the brightness, grouped scale extended in both directions

Sun, m = -26.83 , the faintest objects, m = 30

Proxima Centauri -

Vega m = 0.03

Zeta Reticuli - m = 5.54

colors - grouped

spectral types - grouped

Proxima Centauri - M5V

Sun -

Vega - AOV

Barnard's Star - M4V

Zeta Reticuli -

luminosity classes - grouped

$L=4\pi R^{2}\sigma T_{e}^{4}$

based on Maxwell's equation pertaining to radiation pressure and the laws of thermodynamics, so for a star of spherical radius R and area $A=4\pi R^{2}$ and where$T_{e}$ is the effective temperature of the surface of the star, utilized due to that stars are not perfect blackbodies

Sun, $L=3.839x10^{26}W=L_{\bigodot }$

Vega, $L=37L_{\bigodot }$

Proxima Centauri -$L=6x10^{-6}L_{\bigodot }$

Zeta Reticuli -

Stellar structure

Stars of different mass and age have varying internal structures. Stellar structure models describe the internal structure of a star in detail and make detailed predictions about the luminosity, the color and the future evolution of the star.

Equations of stellar structure

Pressure equilibrium: Pressure and gravity must balance or the star will expand or contract. The balance of the gravity force and the pressure gradient is known as the hydrostatic balance.

${\frac {dP_{r}}{dr}}=-\rho _{r}{\frac {GM_{r}}{r^{2}}}$

Conservation of mass

${\frac {dM_{r}}{dr}}=4\pi r^{2}\rho _{r}$

Energy generation: To keep the temperature constant everywhere luminosity $L$ must be generated.Considering the energy leaving the spherical shell yields the energy equation

${\frac {dL_{r}}{dr}}=4\pi r^{2}\rho _{r}\epsilon$

where $\epsilon$ is the energy generation rate (sum of all energy sources and losses) per g and s

Energy transport: The temperature inside a star must increase progressively towards its center to make energy flow from the center to the surface. The energy transport equation takes differing forms depending upon the mode of energy transport. For the case of convective luminosity transport we have

${\frac {dT_{r}}{dr}}=\left(1-{\frac {1}{\gamma }}\right){\frac {T_{r}}{P_{r}}}{\frac {dP_{r}}{dr}}$

where $\gamma =c_{p}/c_{v}$ is the adiabatic index, the ratio of specific heats in the gas

For radiative energy transport we have

${\frac {dT}{dr}}=-{\frac {3\kappa \rho }{4acT^{3}}}{\frac {L(r)}{4\pi r^{2}}}$

where $\kappa$ is the opacity of the matter and $a$ is the radiation density constant equal to $7.56591\times 10^{-15}erg\ cm^{-3}K^{-4}$

For conductive luminosity transport (appropriate for a white dwarf), the energy equation is

${\frac {dT}{dr}}=-{\frac {1}{k}}{\frac {1}{4\pi r^{2}}}$

where k is the thermal conductivity.

Stellar evolution

The evolution of stars is due to their sustained emission of radiation originating from an internal source. The energy source that supplies the luminosity of stars during most of their lifetimes is nuclear fusion, which turns a small fraction of the rest mass into energy.

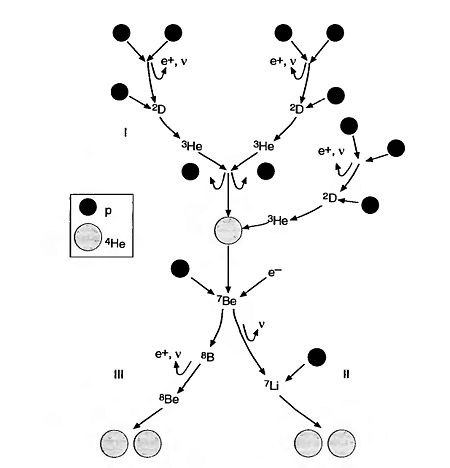
Hydrogen burning I: the p-p chain

Figure 1. The nuclear reactions of the p-p chains: I, II, and III.

The most abundant element in newly born stars is hydrogen. Fusion of hydrogen into the next element, helium, would require an encounter of three or four protons - hydrogen nuclei - within the distances of the order fermis (1E-15 m). The probability of such a multiple encounter is small, therefore this process does not happen at once, but gradually through the chain of reactions. The first link of this chain is the fusion of two protons

$p+p\rightarrow ^{2}D+e^{+}+\nu \ ,$

that forms a stable isotope of hydrogen. Then deuterium captures a proton to form the lighter isotope of helium

$D+p\rightarrow ^{3}He+\gamma \ ,$

where $\gamma$ indicates the emission of an energetic photon that soon will be absorbed by other particles. Now the reaction becomes more complicated: two $^{3}He$ nuclei form the stable isotope of helium, $^{4}He$

$^{3}He+^{3}He\rightarrow ^{4}He+2p\ ,$

and later

$^{3}He+^{4}He\rightarrow ^{7}Be+\gamma \ .$

This is the end of the so called p-p chain I.

The p-p chain II starts with the electron capture by the beryllium nucleus

$^{7}Be+e^{-}\rightarrow ^{7}Li+\nu \ ,$

and then a subsequent capture of the proton

$^{7}Li+p\rightarrow 2^{4}He\ ,$

then ends. The p-p chain III results by capturing proton by beryllium nucleus instead of an electron capture

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ^7Be + p \rightarrow ^8B + \gamma \ . }

Since Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ^8B} is radioactive it decays

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ^8B \rightarrow ^8Be + e^+ + \nu \ , }

and the since Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ^8Be} is highly unstable it goes through the reaction

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ^8Be \rightarrow 2 ^4He \ . }

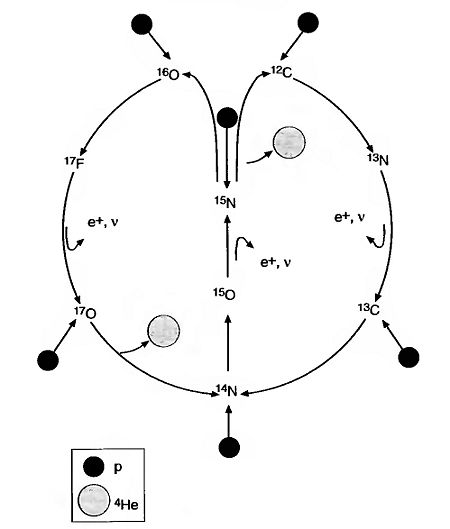
Hydrogen burning II: the CNO bi-cycle

Figure 2. The nuclear reactions of the CNO bi-cycle

The small percentage of initial composition of stars consist of carbon, nitrogen, and oxygen nuclei. These nuclei may induce a chain of reactions that transform the hydrogen into helium. This procedure is first introduced by Bethe and is known as the CNO cycle. Since there are two such cycles, therefore we call it CNO bi-cycle.

The cycle one is as following:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ^{12}C + ^1H \rightarrow ^{13}N + \gamma \ , }

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ^{13}N \rightarrow ^{13}C + e^+ + \nu \ , }

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ^{13}C + ^1H \rightarrow ^{14}N + \gamma \ , }

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ^{14}N + ^1H \rightarrow ^{15}O + \gamma \ , }

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ^{15}O \rightarrow ^{15}N + e^+ + \nu \ , }

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ^{15}N + ^1H \rightarrow ^{12}C + ^4He \ . }

And the cycle two is:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ^{14}N + ^1H \rightarrow ^{15}O + \gamma \ , }

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ^{15}O \rightarrow ^{15}N + e^+ + \nu \ , }

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ^{15}N + ^1H \rightarrow ^{16}O + \gamma \ , }

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ^{16}O + ^1H \rightarrow ^{17}F + \gamma \ , }

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ^{17}F \rightarrow ^{17}O + e^+ + \nu \ , }

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ^{17}O + ^1H \rightarrow ^{14}N + ^4He \ . }