Solution to Set 6

Problem 1.

Given

Aluminum(Al) is trivalent with

• atomic mass $m_{a}=27$ amu
• density $n=2.7g/cm^{3}$
• room temperature $T=293-296.5K$
• mean free time between electron collisions $t_{avg}=4{\rm {x}}10^{-14}$ s.

(a) Resistivity

Calculate the resistivity $\rho$ of aluminum(Al) at room temperature.

$\rho ={\frac {1}{\sigma }}\;$ $={\frac {1}{37.8\times 10^{6}Sm^{-1}}}\;$ $=2.82\times 10^{-8}\;$Ω·m

(b)

b) If a 2-V voltage is applied to the ends of an aluminum wire 10 m long and with a cross- sectional area of $1mm^{2}$, what is the current flowing through it?

Problem 2

The resistivity of a certain material at room temperature is 0.02 Wm and the Hall coefficient is $5{\rm {x}}10^{-4}$ $m^{3}/C$. An electric field of 1 V/m is applied across it. Deduce all the information you can think of about this material.

Problem 3.

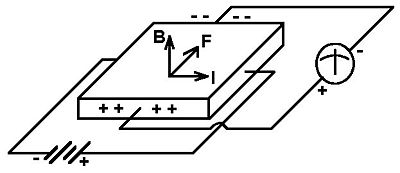
a) Sketch a setup used to measure the Hall effect. Label each part.

b) A semiconductor crystal is 5 mm long, 4 mm wide, and 2 mm thick. A 40mA current flows across the length of the sample after a 2-V battery is connected to the ends. When a 0.1T magnetic field is applied perpendicular to the large surface of the specimen, a Hall voltage of 15mV develops across the width of the sample. Determine the i) conductivity, ii) carrier density, iii) mobility, iv) Fermi velocity, for this semiconductor.

Problem 4

a) Derive the expressions for the Fermi energy, Fermi velocity, and electronic density of states for a two-dimensional free electron gas.

b) A 2D electron gas formed in a GaAs/AlGaAs quantum well has a density of $2{\rm {x}}10^{11}cm^{-2}$. Assuming that the electrons there have the free electron mass, calculate the Fermi energy and Fermi velocity.