Solution to Set 6: Difference between revisions
(→(a)) |
(→(b)) |
||
| Line 14: | Line 14: | ||
<math> = 2.82 \times 10^{-8} \;</math>Ω·m | <math> = 2.82 \times 10^{-8} \;</math>Ω·m | ||
===(b)=== | ===(b) Current === | ||
If a 2-V voltage is applied to the ends of an aluminum wire 10 m long and with a cross- sectional area of <math>1 mm^2</math>, what is the current flowing through it? | |||
<math>R = \frac{\iota \cdot \rho}{A} \;</math> | |||
<math> = \frac{\left (10m \right ) \cdot \left (2.646 \times 10^{-8} \Omega \cdot m \right )}{\left (10^{-6}m \right )} \;</math> | |||
<math> = 0.2646 \Omega \;</math> | |||
==Problem 2== | ==Problem 2== | ||
Revision as of 22:20, 8 April 2009
Problem 1.
Given
Aluminum(Al) is trivalent with
- atomic mass amu
- density
- room temperature
- mean free time between electron collisions s.
(a) Resistivity
Calculate the resistivity of aluminum(Al) at room temperature.
Ω·m
(b) Current
If a 2-V voltage is applied to the ends of an aluminum wire 10 m long and with a cross- sectional area of , what is the current flowing through it?
Problem 2
The resistivity of a certain material at room temperature is 0.02 Wm and the Hall coefficient is . An electric field of 1 V/m is applied across it. Deduce all the information you can think of about this material.
Problem 3.
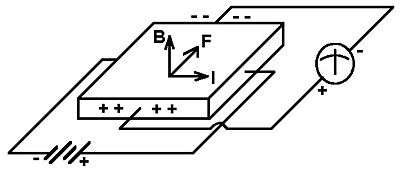
a) Sketch a setup used to measure the Hall effect. Label each part.
b) A semiconductor crystal is 5 mm long, 4 mm wide, and 2 mm thick. A 40mA current flows across the length of the sample after a 2-V battery is connected to the ends. When a 0.1T magnetic field is applied perpendicular to the large surface of the specimen, a Hall voltage of 15mV develops across the width of the sample. Determine the i) conductivity, ii) carrier density, iii) mobility, iv) Fermi velocity, for this semiconductor.
Problem 4
a) Derive the expressions for the Fermi energy, Fermi velocity, and electronic density of states for a two-dimensional free electron gas.
b) A 2D electron gas formed in a GaAs/AlGaAs quantum well has a density of . Assuming that the electrons there have the free electron mass, calculate the Fermi energy and Fermi velocity.