2nd Week: Properties of Astrophysical Plasmas: Difference between revisions
(New page: ==Basic Thermodynamics for Quantum Systems== Particle density: <math>n = \frac{N}{V} =\int_{0}^{\infty }{w(p)f(p)dp}</math> where <math>f(p)</math> is the occupation probability and <mat...) |
|||
| (48 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
[[Image:Main tycho remnant full.jpg|right|right|thumb|300px|The remnant of "Tycho's Supernova", a huge ball of expanding plasma.]] | |||
'''Plasma''' is a state of matter in which the atoms and the molecules are so hot, that they have ionized into negatively charged electrons and positively charged ions. The plasma found in the universe, whose physical properties are studied in astrophysics is known as '''astrophysical plasma'''. To study the properties of astrophysical plasma the equation of state of matter is very important. Here, we will bring some basic tools from thermodynamics and derive the equation of state for non-relativistic and relativistic plasma. | |||
==Basic thermodynamics for quantum systems== | |||
The particle density is determined as follows | |||
<math> n = \frac{N}{V} =\int_{0}^{\infty }{w(p)f(p)dp} \ , </math> | |||
<math>P = \frac{1}{3}\int_{0}^{\infty }{pvw(p)f(p)dp}</math> where <math>p</math> is momentum and <math>v</math> is velocity. | where <math>f(p)</math> is the occupation probability and <math>w(p)</math> is the state density per unit volume. | ||
The energy density is given by | |||
<math> u = \frac{U}{V} =\int_{0}^{\infty }{Ew(p)f(p)dp} \ , </math> | |||
where <math>E</math> in the energy of the particle. | |||
The pressure is defined as | |||
<math>P = \frac{1}{3}\int_{0}^{\infty }{pvw(p)f(p)dp} \ , </math> | |||
where <math>p</math> is the value of the momentum of the particle and <math>v</math> is its velocity. | |||
==Distribution functions== | |||
In statistical physics the density of states of a system describes the number of states at each energy level that are available to be occupied. The general form of the density of state is as follows: | |||
<math>\omega(E) = \frac{d\Phi}{dE} \ , </math> | |||
where <math>\Phi</math> is the number of states. | |||
For the non-relativistic system | |||
<math> \Phi(E) = \frac{4\pi}{3}\frac{g}{h^3}(2mE)^{3/2} \ , </math> | |||
where <math>g=2s+1</math> is the statistical weight. Then the density of state is | |||
<math> \omega(E) = 2 \pi \frac{g}{h^3}(2m)^{3/2}(E)^{1/2} \ . </math> | |||
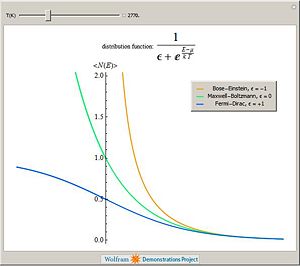
There are four probability distribution functions in statistical physics that are known with infinite support: Gibbs distribution, Maxwell-Boltzmann distribution, Fermi-Dirac distribution and Bose-Einstein distribution. The occupation probability, i.e. the probability of occupation of a given energy states are as follows. | |||
*Maxwell-Boltzmann distribution | |||
<math>f(p)=e^{-\frac{E(p)-\mu}{kT}} \ , </math> | |||
*Bose-Einstein distribution | |||
<math>f(p)=\frac{1}{e^{\frac{E(p)-\mu}{kT}}-1} \ , </math> | |||
*Fermi-Dirac distribution | |||
<math>f(p)=\frac{1}{e^{\frac{E(p)-\mu}{kT}}+1} \ , </math> | |||
where <math>k</math> is the Boltzmann constant. | |||
==Thermodynamical variables and potentials== | |||
Now we provide with the expressions of thermodynamic potentials. The '''internal energy''' is given by | |||
<math>U = TS - PV + \sum_i \mu_i N_i \ , </math> | |||
where <math>T</math> is the temperature, <math>S</math> is the entropy, <math>P</math> is the pressure and <math>V</math> is the volume of the system, while <math>N_i</math> is the number of particles in the state <math>i</math> of the system and <math>\mu_i</math> is is the chemical potential associated to those particles. These quantities are also known as ''thermodynamical variables''. | |||
The so called '''Helmholtz free energy''' is given by | |||
<math>F = U-TS \ . </math> | |||
The enthalpy of the system can be found using the expression | |||
<math>H = U+PV \ .</math> | |||
The '''Gibbs free energy''' is | |||
<math>G = U+PV -TS \ .</math> | |||
The so called '''Landau potential''' is expressed by | |||
<math>\Omega = U-TS-\sum_i \mu_i N_i \ . </math> | |||
==Equation of state== | |||
[[Image:Main popup_13.jpg|right|right|thumb|300px|Comparsion of the Fermi-Dirac, Bose-Einstein, and Boltzmann distributions. All for the same value <math> \mu</math>.]] | |||
In physics equations of state are thermodynamic equations that describe the state of matter under a given set of physical conditions. these equations provide relationships between two or more macroscopically measurable quantities (such as pressure, volume, temperature and Energy) in a given state of matter. | |||
A classic example of an EOS is the Ideal Gas Law by Benoît Paul Émile Clapeyron | |||
<math>{\ pV = nRT} \ .</math> | |||
Important Equations of State for Nuclear Astrophysics as given in class: | |||
Particle density for a given system is | |||
<math>n = \sum{n_i} \ , </math> | |||
<math>n_i = \frac{4\pi g_i}{h^3}\int_{0}^{\infty }{\frac{p_i^2 dp_i}{exp[\frac{E_i-\mu_i}{kT}]\pm 1}} \ ,</math> | |||
where <math>E_i = \sqrt{p_i^2c^2 + (m_ic^2)^2}</math> in general. | |||
Pressure for a given system is | |||
<math>P = \sum{P_i} \ , </math> | |||
<math>P_i = \frac{4\pi c^2g_i}{3h^3}\int_{0}^{\infty }{\frac{p_i^4 dp_i}{E_i(exp[\frac{E_i-\mu_i}{kT}]\pm 1)}} \ .</math> | |||
===Photon Gas=== | |||
A photon is a particle viewed as an elementary form of radiation on the electromagnetic spectrum. Although, photons behave as both a particle and a wave so giving rise to particle-wave duality. They have integer spin,so being a boson. As a result must obey Bose-Einstein statistics. | |||
===Boltzmann Gas=== | |||
A gas treated as ideal that obeys all gas laws for simplification of calculations. Even though all known gases are not ideal. In such gas, particles are considered to not interact with one another and these processes are point-like particles. | |||
===Non relativistic, Degenerate Fermi Gas=== | |||
When, | |||
: <math>kT<<\mu \ , </math> | |||
where | |||
:<math>\mu = \frac{\partial F }{\partial N}_{T,V} \ .</math> | |||
then ... | |||
Latest revision as of 10:50, 12 April 2009
Plasma is a state of matter in which the atoms and the molecules are so hot, that they have ionized into negatively charged electrons and positively charged ions. The plasma found in the universe, whose physical properties are studied in astrophysics is known as astrophysical plasma. To study the properties of astrophysical plasma the equation of state of matter is very important. Here, we will bring some basic tools from thermodynamics and derive the equation of state for non-relativistic and relativistic plasma.
Basic thermodynamics for quantum systems
The particle density is determined as follows
where is the occupation probability and is the state density per unit volume.
The energy density is given by
where in the energy of the particle.
The pressure is defined as
where is the value of the momentum of the particle and is its velocity.
Distribution functions
In statistical physics the density of states of a system describes the number of states at each energy level that are available to be occupied. The general form of the density of state is as follows:
where is the number of states.
For the non-relativistic system
where is the statistical weight. Then the density of state is
There are four probability distribution functions in statistical physics that are known with infinite support: Gibbs distribution, Maxwell-Boltzmann distribution, Fermi-Dirac distribution and Bose-Einstein distribution. The occupation probability, i.e. the probability of occupation of a given energy states are as follows.
- Maxwell-Boltzmann distribution
- Bose-Einstein distribution
- Fermi-Dirac distribution
where is the Boltzmann constant.
Thermodynamical variables and potentials
Now we provide with the expressions of thermodynamic potentials. The internal energy is given by
where is the temperature, is the entropy, is the pressure and is the volume of the system, while is the number of particles in the state of the system and is is the chemical potential associated to those particles. These quantities are also known as thermodynamical variables.
The so called Helmholtz free energy is given by
The enthalpy of the system can be found using the expression
The Gibbs free energy is
The so called Landau potential is expressed by
Equation of state
In physics equations of state are thermodynamic equations that describe the state of matter under a given set of physical conditions. these equations provide relationships between two or more macroscopically measurable quantities (such as pressure, volume, temperature and Energy) in a given state of matter.
A classic example of an EOS is the Ideal Gas Law by Benoît Paul Émile Clapeyron
Important Equations of State for Nuclear Astrophysics as given in class:
Particle density for a given system is
where in general.
Pressure for a given system is
Photon Gas
A photon is a particle viewed as an elementary form of radiation on the electromagnetic spectrum. Although, photons behave as both a particle and a wave so giving rise to particle-wave duality. They have integer spin,so being a boson. As a result must obey Bose-Einstein statistics.
Boltzmann Gas
A gas treated as ideal that obeys all gas laws for simplification of calculations. Even though all known gases are not ideal. In such gas, particles are considered to not interact with one another and these processes are point-like particles.
Non relativistic, Degenerate Fermi Gas
When,
where
then ...

































![{\displaystyle n_{i}={\frac {4\pi g_{i}}{h^{3}}}\int _{0}^{\infty }{\frac {p_{i}^{2}dp_{i}}{exp[{\frac {E_{i}-\mu _{i}}{kT}}]\pm 1}}\ ,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/56255f38c488d9b1a0e6b4aee97efd6a4ce1d894)


![{\displaystyle P_{i}={\frac {4\pi c^{2}g_{i}}{3h^{3}}}\int _{0}^{\infty }{\frac {p_{i}^{4}dp_{i}}{E_{i}(exp[{\frac {E_{i}-\mu _{i}}{kT}}]\pm 1)}}\ .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2baab06597f4e245884a524344d90dad5b92425d)

