Experimental methods for determining crystal structure

Scattering Methods

There are various different techniques that are employed to probe the interior structure of the microscopic. Most make use of scattering described by Bragg's Law, bouncing various particles or waves off of the atoms that make up the target sample. This is an elastic scattering, where the wavelength of the wave after collision is the same as that of the incoming wave. Additionally, for such scattering to be effective in producing a diffraction pattern that can be analyzed, the waves, once scattered off atomic centers need to not scatter additional times.

This is called secondary scattering, if the incident waves interact too strongly with the sample crystal, the secondary scattering caused will create a diffraction pattern that is difficult to analyze because the periodic pattern originally created from the corresponding periodic array of atoms will be altered dramatically. From the distribution of spots on a film representing the points of constructive interference, the location of the atoms can be visually represented.

Different waves or particles (as quantum wave-particle duality shows how all particles can be represented as waves, and conversely, waves can be represented as particles) will have different qualities that effect how they will scatter. Some of the common waves and particles used in scattering techniques are X-rays, electrons, and neutrons.

Bragg's Law

A visual depiction of the relation of wavelength, atomic spacing, and scattering angle.

The core principle behind using waves scattered off atomic centers to obtain information about the internal structure of a crystal is that of Bragg's Law. It was developed by William Lawrence Bragg around the turn of the 20th century, along with his father William Henry Bragg. They shared a Nobel prize for this work in 1915.

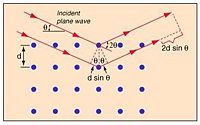
Bragg's Law gives a relation between wavelength of the incident waves which are being used to scatter $\lambda$, the distance between the scattering centers, in this case, the atomic nuclei $d$, and the angle between the waves and the plane formed by the atoms in the lattice $\theta$.

Constructive interference occurs when the path difference between the two waves is an integer number of wavelengths, so they have the same phase at that point.

So, from the diagram to the right, constructive interference will be observed when,

$n\lambda =2x$

where x is the length of the smaller leg of the triangle formed by the distance between atoms, and the perpendicular between waves. This distance that the second wave travels represents half of the total path difference between the two waves.

$x=d*sin(\theta )$

so,

$n\lambda =2d*sin(\theta )$

When the incident waves hit the plane formed by the atomic centers, they reflect or transmit and can interfere either constructively or destructively. In this way, the crystal lattice acts as a diffraction grating. Where the waves constructively interfere, a film placed in the path of the waves will record a dot, and places with destructive interference record nothing. Doing this sort of scattering process from many different, regular angles will give a 3-D pattern representing the location of atoms in the lattice.

X-ray scattering

In this method, electromagnetic waves, specifically monochromatic X-rays (X-rays of the same wavelength), are shot at a crystal sample that will act as a diffraction grating because of the periodic arrangement of atoms in crystal. The points recorded on some sort of film behind it will represent constructive interference, and by recording sufficiently many sets of reflections (the projected spots where constructive interference happens) from different angles, one can derive the arrangement of the lattice that created the reflections.

The reason X-rays are used for this instead of some other form of electromagnetic radiation, say, for example, visible light, is an issue of wavelength. X-rays have a wavelength in the range of 0.01-10nm range, visible light on the other hand has a wavelength around 4000-7000nm. More than 5 orders of magnitude separation. Why does this difference matter? Because of the separation distance between atoms in the crystal lattice. If you tried to use a crystal as a diffraction grating with visible light, the wavelength would be so much larger than the distance between scattering centers that you wouldn't nearly scatter from enough points with the visible light waves to get the information you wanted.

Because of this X-rays, who have wavelength comparable to the characteristic distance between atoms (a few Angstroms, Å) are a much better choice. Since their wavelength is around the same scale as the space between atomic centers in a crystal, the wave has the chance to scatter off them in a much more regular fashion, as opposed to visible light which might pass 1000 atoms in a single wavelength.

From the reflections created by the diffraction at various different, regular angles, you can determine the density of electrons in the sample crystal, and from this, you can determine information about the sample crystal, whether it is intermolecular spacing, chemical bonding, or its disorder.

Electron scattering

Because of the wave nature of electrons, they can also be scattered off atoms in a crystal lattice. This process is similar to X-ray scattering. Some differences are that

1. Electrons used in this way have a smaller wavelength than X-rays, this allows for greater resolution.
2. The thickness of the sample must be very small to be transparent with respect to the electrons, on the order of ~100nm. This is because, unlike X-rays, electrons are much more likely to undergo secondary scattering. Decreasing the thickness of the sample prevents the scattered electrons from re-scattering and creating a diffraction pattern that is difficult to analyze.
3. Whereas X-rays interact with the spatial arrangement of atoms in a lattice (photons have no charge), electrons are charged particles. Because of this, they interact with the charged centers and electrons of the sample.

The source of electrons that are scattered in this way is commonly a Transmission Electron Microscope (TEM), or Scanning Electron Microscope (SEM). A SEM generally uses a potential around 10kV, this voltage accelerates electrons used in this way to around 0.2c (c = speed of light, $3*10^{8}m/s$). A TEM uses a larger potential of ~200kV, this higher voltage accelerates electrons to closer to 0.7c.

Electrons fired at a target from a SEM or TEM will have a much larger wavelength than X-ray used for X-ray diffraction, using the de Broglie wave $\lambda ={\frac {h}{p}}$

and actually are energetic enough to require a relativistic adjustment giving the form,

$\lambda ={\frac {h}{\sqrt {2m_{e}eU+{\frac {e^{2}U^{2}}{c^{2}}}}}}$

where $\lambda$ is wavelength, $h$ is Planck's constant, $m_{e}$ is the mass of the electron, and $U$ is the potential used to accelerate the electrons.

Using this formula one finds the wavelength of the fired electrons to be ~10pm for the SEM and ~2pm for the TEM. Comparing this to the X-rays used in X-ray diffraction with wavelength of ~100pm (0.1nm), its easy to see this scattering method can provide a higher resolution. However, the downside to this method is of course that the sample must be extremely thin and is more likely to undergo radiation damage from being bombarded with energetic electrons

Neutron diffraction

Similar to electron and X-ray diffraction, neutrons with wavelength ~0.1nm are used to scatter off atomic centers in a crystal to create a pattern from which its atomic structure can be derived.