Klein-Gordon equation: Difference between revisions
| (9 intermediate revisions by 3 users not shown) | |||
| Line 6: | Line 6: | ||
Substituting <math>E \rightarrow i\hbar \frac{\partial}{\partial t}</math> and <math>\bold p \rightarrow -i\hbar \nabla</math>, we get Klein-Gordon equation for free particles as follows: | Substituting <math>E \rightarrow i\hbar \frac{\partial}{\partial t}</math> and <math>\bold p \rightarrow -i\hbar \nabla</math>, we get Klein-Gordon equation for free particles as follows: | ||
<math>-\hbar^2 \frac{\partial ^2\psi(\bold r, t)}{\partial t^2}=(-\hbar^2c^2\nabla^2+m^2c^4)\psi(\bold r, t)\qquad \qquad \qquad \qquad \qquad (1)</math> | <math>-\hbar^2 \frac{\partial ^2\psi(\bold r, t)}{\partial t^2}=(-\hbar^2c^2\nabla^2+m^2c^4)\psi(\bold r, t)\qquad \qquad \qquad \qquad \qquad (9.1.1)</math> | ||
Klein-Gordon can also be written as the following: | Klein-Gordon can also be written as the following: | ||
<span id="9.1.2"></span> | |||
<math>(\square-K^2)\psi(\bold r, t)=0\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \;\;\;\;(2)</math> | <math>(\square-K^2)\psi(\bold r, t)=0\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \;\;\;\;(9.1.2)</math> | ||
where <math>\square=\nabla^2-\frac{1}{c^2}\frac{\partial^2}{\partial t^2}</math> is d'Alembert operator and <math>K=\frac{mc}{\hbar}</math>. | where <math>\square=\nabla^2-\frac{1}{c^2}\frac{\partial^2}{\partial t^2}</math> is d'Alembert operator and <math>K=\frac{mc}{\hbar}</math>. | ||
Equation | Equation [[#9.1.2]] looks like a classical wave equation with an extra term <math>K^2</math>. | ||
Potentials couple to the Klein-Gordon equation in a manner analogous to classical four-vectors. A good example of this is the potential four-vector: | Potentials couple to the Klein-Gordon equation in a manner analogous to classical four-vectors. A good example of this is the potential four-vector: | ||
| Line 28: | Line 28: | ||
<math>P^{\mu} = p^{\mu}-\frac{e}{c}\Phi^{\mu} = ( \frac{E}{c}-\frac{e}{c}\phi ; \bold{p}-\frac{e}{c}\bold{A} )</math> | <math>P^{\mu} = p^{\mu}-\frac{e}{c}\Phi^{\mu} = ( \frac{E}{c}-\frac{e}{c}\phi ; \bold{p}-\frac{e}{c}\bold{A} )</math> | ||
Squaring the conjugate momentum four vector and multiplying by <math>c^2</math>, we obtain the Klein-Gordon equation in an electromagnetic field by moving to the quantum limit and acting on <math>\psi </math>: | Squaring the conjugate momentum four vector and multiplying by <math>c^2</math>, we obtain the Klein-Gordon equation in an electromagnetic field by moving to the quantum limit and acting on <math>\displaystyle{\psi}</math>: | ||
<math>c^2 P^{\mu}P_{\mu} = m^2 c^4 = (E-e\phi)^2-(c\bold{p}-e\bold{A})^2</math> | <math>c^2 P^{\mu}P_{\mu} = m^2 c^4 = (E-e\phi)^2-(c\bold{p}-e\bold{A})^2</math> | ||
<span id="9.1.3"></span> | |||
<math>\Rightarrow\left[ i\hbar \frac {\partial}{\partial t}-e\phi(\bold r, t) \right] ^2\psi(\bold r, t)=\left( \left[ -i\hbar\nabla-\frac{e}{c}\bold A(\bold r, t)\right] ^2c^2+m^2c^4\right) \psi(\bold r, t)</math> | <math>\Rightarrow\left[ i\hbar \frac {\partial}{\partial t}-e\phi(\bold r, t) \right] ^2\psi(\bold r, t)=\left( \left[ -i\hbar\nabla-\frac{e}{c}\bold A(\bold r, t)\right] ^2c^2+m^2c^4\right) \psi(\bold r, t)\qquad \qquad (9.1.3)</math> | ||
The Klein-Gordon equation is second order in time. Therefore, to see how the states of a system evolve in time we need to know both <math>\psi(\bold r, t)</math> and <math>\frac{\partial\psi(\bold r, t)}{\partial t}</math> at a certain time. While in nonrelativistic quantum mechanics, we only need <math>\psi(\bold r, t)</math> | The Klein-Gordon equation is second order in time. Therefore, to see how the states of a system evolve in time we need to know both <math>\psi(\bold r, t)</math> and <math>\frac{\partial\psi(\bold r, t)}{\partial t}</math> at a certain time. While in nonrelativistic quantum mechanics, we only need <math>\psi(\bold r, t)</math> | ||
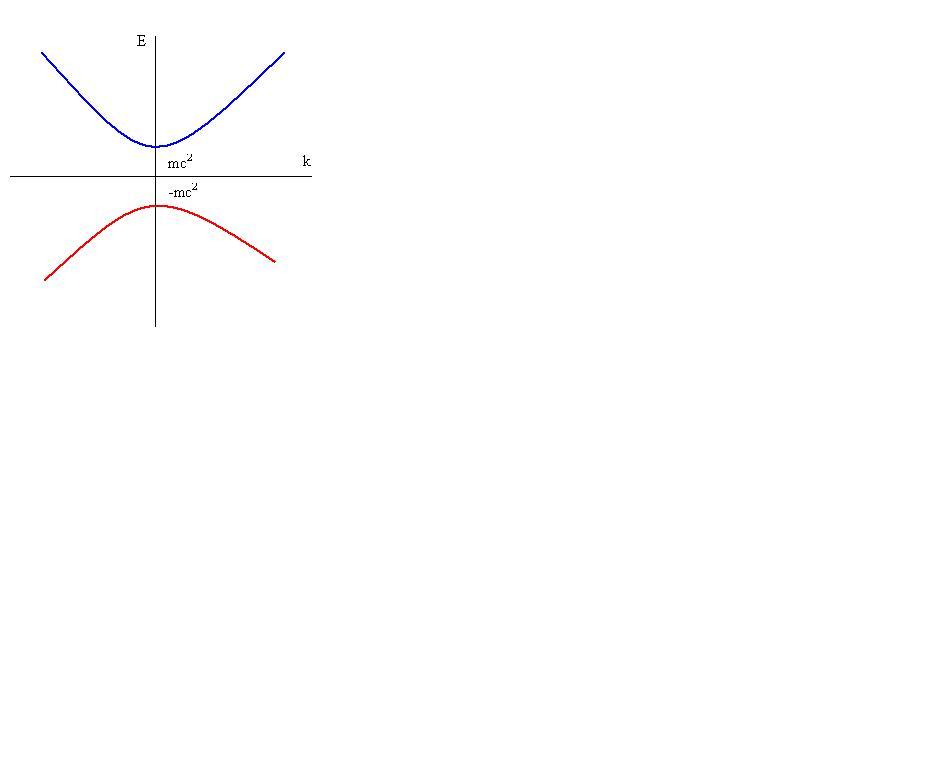
Also because the Klein-Gordon equation is second order in time, it has the solutions <math>\psi(\bold r, t)=e^{i(\bold p \bold r - Et)/\hbar}</math> with either sign of energy <math>E=\pm c\sqrt{\bold p^2+m^2c^2}</math>. The negative energy solution of Klein-Gordon equation has a strange property that the energy decreases as the magnitude of the momentum increases. We will see that the negative energy solutions of Klein-Gordon equation describe antiparticles, while the positive energy solutions describe particles. | Also because the Klein-Gordon equation is second order in time, it has the solutions <math>\psi(\bold r, t)=e^{i(\bold p \bold r - Et)/\hbar}</math> with either sign of energy <math>E=\pm c\sqrt{\bold p^2+m^2c^2}</math>. The negative energy solution of Klein-Gordon equation has a strange property that the energy decreases as the magnitude of the momentum increases. We will see that the negative energy solutions of Klein-Gordon equation describe antiparticles, while the positive energy solutions describe particles. | ||
Below is an image depicting the two different enery levels (positive and negative). | |||
[[Image:KleinGordonEnergy.JPG]] | |||
==Continuity equation== | ==Continuity equation== | ||
Multiplying (1) by <math>\bold \psi^{*}</math> from the left, we get: | Multiplying (1) by <math>\bold \psi^{*}</math> from the left, we get: | ||
<span id="9.2.1"></span> | |||
<math>-\frac{\hbar^2}{c^2}\psi^{*} \frac{\partial ^2\psi(\bold r, t)}{\partial t^2}=\psi^{*}(-\hbar^2\nabla^2+m^2c^2)\psi(\bold r, t)\qquad \qquad \qquad ( | <math>-\frac{\hbar^2}{c^2}\psi^{*} \frac{\partial ^2\psi(\bold r, t)}{\partial t^2}=\psi^{*}(-\hbar^2\nabla^2+m^2c^2)\psi(\bold r, t)\qquad \qquad \qquad (9.2.1)</math> | ||
Multiplying the complex conjugate form of (1) by <math>\bold \psi</math> from the left, we get: | Multiplying the complex conjugate form of (1) by <math>\bold \psi</math> from the left, we get: | ||
<span id="9.2.2"></span> | |||
<math>-\frac{\hbar^2}{c^2}\psi \frac{\partial ^2\psi^{*}(\bold r, t)}{\partial t^2}=\psi(-\hbar^2\nabla^2+m^2c^2)\psi^{*}(\bold r, t)\qquad \qquad \qquad (9.2.2)</math> | |||
Subtracting [[#9.2.2]] from [[#9.2.1]], we get: | |||
<math>-\frac{\hbar^2}{c^2}\left( \psi^{*} \frac{\partial ^2\psi}{\partial t^2}-\psi \frac{\partial ^2\psi^{*}}{\partial t^2}\right) =\hbar^2\left( \psi\nabla^2\psi^{*}-\psi^{*}\nabla^2\psi\right) </math> | <math>-\frac{\hbar^2}{c^2}\left( \psi^{*} \frac{\partial ^2\psi}{\partial t^2}-\psi \frac{\partial ^2\psi^{*}}{\partial t^2}\right) =\hbar^2\left( \psi\nabla^2\psi^{*}-\psi^{*}\nabla^2\psi\right) </math> | ||
| Line 56: | Line 60: | ||
this give us the continuity equation: | this give us the continuity equation: | ||
<span id="9.2.3"></span> | |||
<math>\frac {\partial \rho}{\partial t}+\nabla \bold j = 0 \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad(9.2.3)</math> | |||
where <math>\rho = \frac {i\hbar}{2mc^2}\left( \psi^{*}\frac{\partial\psi}{\partial t}-\psi\frac{\partial\psi^{*}}{\partial t}\right) \qquad \qquad \qquad \qquad \qquad \; \; \; \;(9.2.4)</math> | |||
where <math>\rho = \frac {i\hbar}{2mc^2}\left( \psi^{*}\frac{\partial\psi}{\partial t}-\psi\frac{\partial\psi^{*}}{\partial t}\right) \qquad \qquad \qquad \qquad \qquad \; \; \; \;( | |||
<math>\bold j = \frac {\hbar}{2mi}(\psi^{*}\nabla\psi-\psi\nabla\psi^{*})\qquad \qquad \qquad \qquad \qquad \qquad \qquad \; \;( | <math>\bold j = \frac {\hbar}{2mi}(\psi^{*}\nabla\psi-\psi\nabla\psi^{*})\qquad \qquad \qquad \qquad \qquad \qquad \qquad \; \;(9.2.5)</math> | ||
From | From [[#9.2.3]] we can see that the integral of the density <math>\bold \rho</math> over all space is conserved. However, <math>\bold\rho</math> is not positively definite. Therefore, we can neither interpret <math>\bold \rho</math> as the particle probability density nor can we interpret <math>\bold j</math> as the particle current. The appropriate interpretation are charge density for <math>e\rho(\bold r,t)</math> and electric current for <math>e\bold j(\bold r, t)</math> since charge density and electric current can be either positive or negative. | ||
Using | Using [[#9.1.3]] and the same procedure as before, it can be shown that the continuity equation still holds in an electromagnetic field with | ||
<math>\bold{j} (\bold{r} , t) = \frac{1}{2m} [\psi^{*}(-i\hbar \bold{\nabla} - \frac{e}{c} \bold{A} )\psi - \psi(-i\hbar \bold{\nabla} + \frac{e}{c} \bold{A} )\psi^{*}]</math> | <math>\bold{j} (\bold{r} , t) = \frac{1}{2m} [\psi^{*}(-i\hbar \bold{\nabla} - \frac{e}{c} \bold{A} )\psi - \psi(-i\hbar \bold{\nabla} + \frac{e}{c} \bold{A} )\psi^{*}]\qquad \ \ (9.2.6)</math> | ||
and | and | ||
<math>\rho (\bold{r} , t) = \frac{1}{2mc^2} [\psi^{*}(i\hbar \frac{\partial}{\partial t} - e\phi )\psi - \psi(i\hbar \frac{\partial}{\partial t} + e\phi )\psi^{*}]</math> | <math>\rho (\bold{r} , t) = \frac{1}{2mc^2} [\psi^{*}(i\hbar \frac{\partial}{\partial t} - e\phi )\psi - \psi(i\hbar \frac{\partial}{\partial t} + e\phi )\psi^{*}]\qquad \ \ \ (9.2.10)</math> | ||
==Nonrelativistic limit== | ==Nonrelativistic limit== | ||
| Line 142: | Line 146: | ||
Now suppose that <math>v(\rho ) = \sum_{k=0}^{\infty} a_k \rho ^k</math>. Putting this solution of R into the radial equation and simplifying, we find that <math>\displaystyle{a_k}</math> follows a recursive relation implying that <math>\displaystyle{\lambda = N+s+1}</math> where N is a constant, and that <math>v(\rho ) = _{1}F_{1}(-N; \ 2(s+1); \ \rho )</math>. Thus, | Now suppose that <math>v(\rho ) = \sum_{k=0}^{\infty} a_k \rho ^k</math>. Putting this solution of R into the radial equation and simplifying, we find that <math>\displaystyle{a_k}</math> follows a recursive relation implying that <math>\displaystyle{\lambda = N+s+1}</math> where N is a constant, and that <math>v(\rho ) = _{1}F_{1}(-N; \ 2(s+1); \ \rho )</math>. Thus, | ||
<math>\psi (\bold{r} , t) = \rho ^s e^{-\frac{\rho}{2}} \ _{1}F_{1}(-N; \ 2(s+1); \ \rho )Y_{\ell m}(\theta , \phi ) e^{-\frac{i}{\hbar}Et}</math> | <math>\psi (\bold{r} , t) = \rho ^s e^{-\frac{\rho}{2}} \ _{1}F_{1}(-N; \ 2(s+1); \ \rho )Y_{\ell m}(\theta , \phi ) e^{-\frac{i}{\hbar}Et}\qquad \ \ (9.5.1)</math> | ||
and | and | ||
<span id="9.5.2"></span> | |||
<math>E_{n \prime}=mc^2 (1+\frac{\gamma ^2}{n \prime ^2})^{-\frac{1}{2}}\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad(9.5.2)</math> | |||
where <math>n \prime = N+s+1</math>. If we expand the root in [[#9.5.2]], we find | |||
If we expand the root in | |||
<math>E_n = mc^2 [1- \frac{\gamma ^2}{2n^2} - \frac{\gamma ^4}{2n^4}(\frac{n}{\ell +\frac{1}{2}} - \frac{3}{4}) +...] = mc^2 - \frac{Ry}{n^2} - \frac{\gamma ^4 mc^2}{2n^4}(\frac{n}{\ell +\frac{1}{2}} - \frac{3}{4}) +...</math>, where <math>\displaystyle{n=N+\ell +1}</math>, as in the non-relativistic case. | <math>E_n = mc^2 [1- \frac{\gamma ^2}{2n^2} - \frac{\gamma ^4}{2n^4}(\frac{n}{\ell +\frac{1}{2}} - \frac{3}{4}) +...] = mc^2 - \frac{Ry}{n^2} - \frac{\gamma ^4 mc^2}{2n^4}(\frac{n}{\ell +\frac{1}{2}} - \frac{3}{4}) +...</math>, where <math>\displaystyle{n=N+\ell +1}</math>, as in the non-relativistic case. | ||
Analyzing the energy states, we see that the first term is the rest mass energy of the particle, the second term is the non-relativistic energy levels of the Coulomb potential, and the third term is the fine structure correction. It should be noted that the Klein-Gordon equation is not compatible with spin. As should be observed, the fine structure correction to a particle with spin in a Coulomb potential is <math>\frac{\gamma ^4 mc^2}{2n^4}(\frac{n}{j+\frac{1}{2}} - \frac{3}{4})</math>, where j is the total angular momentum. The reason we can never reach this correction from the Klein-Gordon equation is because spin has no equivalent four-vector, and so will not couple completely to the Klein-Gordon equation. In order to accommodate spin in any potential, we must use something else. For spin-1/2, that something else is the Dirac equation. | Analyzing the energy states, we see that the first term is the rest mass energy of the particle, the second term is the non-relativistic energy levels of the Coulomb potential, and the third term is the fine structure correction. It should be noted that the Klein-Gordon equation is not compatible with spin. As should be observed, the fine structure correction to a particle with spin in a Coulomb potential is <math>\frac{\gamma ^4 mc^2}{2n^4}(\frac{n}{j+\frac{1}{2}} - \frac{3}{4})</math>, where j is the total angular momentum. The reason we can never reach this correction from the Klein-Gordon equation is because spin has no equivalent four-vector, and so will not couple completely to the Klein-Gordon equation. In order to accommodate spin in any potential, we must use something else. For spin-1/2, that something else is the Dirac equation. | ||
Latest revision as of 16:08, 1 May 2009
How to construct
Starting from the relativistic connection between energy and momentum:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E^2=\bold p^2c^2+m^2c^4}
Substituting Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E \rightarrow i\hbar \frac{\partial}{\partial t}} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bold p \rightarrow -i\hbar \nabla} , we get Klein-Gordon equation for free particles as follows:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -\hbar^2 \frac{\partial ^2\psi(\bold r, t)}{\partial t^2}=(-\hbar^2c^2\nabla^2+m^2c^4)\psi(\bold r, t)\qquad \qquad \qquad \qquad \qquad (9.1.1)}
Klein-Gordon can also be written as the following: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (\square-K^2)\psi(\bold r, t)=0\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \;\;\;\;(9.1.2)}
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \square=\nabla^2-\frac{1}{c^2}\frac{\partial^2}{\partial t^2}} is d'Alembert operator and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle K=\frac{mc}{\hbar}} .
Equation #9.1.2 looks like a classical wave equation with an extra term Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle K^2} .
Potentials couple to the Klein-Gordon equation in a manner analogous to classical four-vectors. A good example of this is the potential four-vector:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi ^{ \mu } = (\phi ; \bold{A} )}
Coupling this to the momentum four-vector,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p ^{ \mu } = (\frac{E}{c} ; \bold{p} )}
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E \rightarrow i\hbar \frac{\partial}{\partial t}} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bold{p} \rightarrow -i\hbar \bold{\nabla}} in the quantum limit, we find the conjugate momentum four vector:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P^{\mu} = p^{\mu}-\frac{e}{c}\Phi^{\mu} = ( \frac{E}{c}-\frac{e}{c}\phi ; \bold{p}-\frac{e}{c}\bold{A} )}
Squaring the conjugate momentum four vector and multiplying by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c^2} , we obtain the Klein-Gordon equation in an electromagnetic field by moving to the quantum limit and acting on Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle{\psi}} :
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c^2 P^{\mu}P_{\mu} = m^2 c^4 = (E-e\phi)^2-(c\bold{p}-e\bold{A})^2} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Rightarrow\left[ i\hbar \frac {\partial}{\partial t}-e\phi(\bold r, t) \right] ^2\psi(\bold r, t)=\left( \left[ -i\hbar\nabla-\frac{e}{c}\bold A(\bold r, t)\right] ^2c^2+m^2c^4\right) \psi(\bold r, t)\qquad \qquad (9.1.3)}
The Klein-Gordon equation is second order in time. Therefore, to see how the states of a system evolve in time we need to know both Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi(\bold r, t)} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial\psi(\bold r, t)}{\partial t}} at a certain time. While in nonrelativistic quantum mechanics, we only need Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi(\bold r, t)}
Also because the Klein-Gordon equation is second order in time, it has the solutions Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi(\bold r, t)=e^{i(\bold p \bold r - Et)/\hbar}} with either sign of energy Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E=\pm c\sqrt{\bold p^2+m^2c^2}} . The negative energy solution of Klein-Gordon equation has a strange property that the energy decreases as the magnitude of the momentum increases. We will see that the negative energy solutions of Klein-Gordon equation describe antiparticles, while the positive energy solutions describe particles.
Below is an image depicting the two different enery levels (positive and negative).
Continuity equation
Multiplying (1) by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bold \psi^{*}} from the left, we get: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -\frac{\hbar^2}{c^2}\psi^{*} \frac{\partial ^2\psi(\bold r, t)}{\partial t^2}=\psi^{*}(-\hbar^2\nabla^2+m^2c^2)\psi(\bold r, t)\qquad \qquad \qquad (9.2.1)}
Multiplying the complex conjugate form of (1) by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bold \psi} from the left, we get: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -\frac{\hbar^2}{c^2}\psi \frac{\partial ^2\psi^{*}(\bold r, t)}{\partial t^2}=\psi(-\hbar^2\nabla^2+m^2c^2)\psi^{*}(\bold r, t)\qquad \qquad \qquad (9.2.2)}
Subtracting #9.2.2 from #9.2.1, we get:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -\frac{\hbar^2}{c^2}\left( \psi^{*} \frac{\partial ^2\psi}{\partial t^2}-\psi \frac{\partial ^2\psi^{*}}{\partial t^2}\right) =\hbar^2\left( \psi\nabla^2\psi^{*}-\psi^{*}\nabla^2\psi\right) }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Rightarrow -\frac{\hbar^2}{c^2}\frac{\partial}{\partial t}\left( \psi^{*}\frac{\partial\psi}{\partial t}-\psi\frac{\partial\psi^{*}}{\partial t}\right) +\hbar^2\nabla\left( \psi^{*}\nabla\psi-\psi\nabla\psi^{*}\right) =0}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Rightarrow \frac {\partial}{\partial t}\left[ \frac {i\hbar}{2mc^2}\left( \psi^{*}\frac{\partial\psi}{\partial t}-\psi\frac{\partial\psi^{*}}{\partial t}\right) \right] +\nabla \left[ \frac {\hbar}{2mi}\left( \psi^{*}\nabla\psi-\psi\nabla\psi^{*}\right) \right] =0}
this give us the continuity equation: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac {\partial \rho}{\partial t}+\nabla \bold j = 0 \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad(9.2.3)}
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho = \frac {i\hbar}{2mc^2}\left( \psi^{*}\frac{\partial\psi}{\partial t}-\psi\frac{\partial\psi^{*}}{\partial t}\right) \qquad \qquad \qquad \qquad \qquad \; \; \; \;(9.2.4)}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bold j = \frac {\hbar}{2mi}(\psi^{*}\nabla\psi-\psi\nabla\psi^{*})\qquad \qquad \qquad \qquad \qquad \qquad \qquad \; \;(9.2.5)}
From #9.2.3 we can see that the integral of the density Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bold \rho} over all space is conserved. However, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bold\rho} is not positively definite. Therefore, we can neither interpret Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bold \rho} as the particle probability density nor can we interpret Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bold j} as the particle current. The appropriate interpretation are charge density for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e\rho(\bold r,t)} and electric current for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e\bold j(\bold r, t)} since charge density and electric current can be either positive or negative.
Using #9.1.3 and the same procedure as before, it can be shown that the continuity equation still holds in an electromagnetic field with
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bold{j} (\bold{r} , t) = \frac{1}{2m} [\psi^{*}(-i\hbar \bold{\nabla} - \frac{e}{c} \bold{A} )\psi - \psi(-i\hbar \bold{\nabla} + \frac{e}{c} \bold{A} )\psi^{*}]\qquad \ \ (9.2.6)}
and
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho (\bold{r} , t) = \frac{1}{2mc^2} [\psi^{*}(i\hbar \frac{\partial}{\partial t} - e\phi )\psi - \psi(i\hbar \frac{\partial}{\partial t} + e\phi )\psi^{*}]\qquad \ \ \ (9.2.10)}
Nonrelativistic limit
In nonrelativistic limit when Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle v \ll c} or Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p \ll mc} , we have:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E=[(pc)^2+(mc^2)^2]^{1/2}=mc^2\left[ 1+(\frac{p}{mc})^2\right] ^{1/2}\approx mc^2\left( 1+\frac{1}{2}\left( \frac{p}{mc}\right) ^2\right) =mc^2+\frac{p^2}{2m}}
So, the relativistic energy is different from classical energy by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle mc^2} , therefore, we can expect that if we write the solution of Klein-Gordon equation as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi e^{-imc^2t/\hbar}} and substitute it into Klein-Gordon equation, we will get Schrodinger equation for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bold \psi} .
Indeed, doing so we get:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -\hbar ^2\frac {\partial ^2 \psi}{\partial t^2}e^{-imc^2t/\hbar}+2\frac {\partial \psi}{\partial t}imc^2 \hbar e^{-imc^2t/\hbar}+\psi m^2c^4 e^{-imc^2t/\hbar}=-\hbar ^2 c^2\nabla ^2 \psi e^{-imc^2t/\hbar}+m^2c^4 \psi e^{-imc^2t/\hbar}}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Rightarrow -\frac {\hbar ^2}{2mc^2} \frac{\partial ^2 \psi}{\partial t^2}+i\hbar \frac {\partial \psi}{\partial t}=-\frac {\hbar ^2}{2m}\nabla ^2 \psi}
In the nonrelativistic limit the first term is considered negligibly small. As a result, for free particles in this limit we get back the Schrodinger equation:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i\hbar \frac {\partial \psi}{\partial t}=-\frac {\hbar ^2}{2m} \nabla ^2 \psi}
Negative energy states and antiparticles
The solutions to the Klein-Gordon equation allow for both positive and negative energies. The positive energies are no cause for concern, but the negative energies seem counter-intuitive classically, as they allow for negative probability densities, spontaneous transitions from the positive energy states to the negative energy states, and particles to propagate both directions in time. We can't simply "drop" the negative energy states, as they form part of the complete set of solutions. One way to interpret these negative energies was proposed by Stükelberg and Feynman: The negative energy solutions describe positive energy antiparticles, which are conjugates to particles and have been experimentally observed.
By observing the Klein-Gordon equation with negative energy states, we can observe some properties of antiparticles. Consider a free particle at rest (Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bold{p} = 0} ). The solution to the Klein-Gordon equation in a rest frame K is then
If we now follow this same procedure for a negative energy state, the free particle wavefunction will be
Notice that the wavefunction for the negative energy state is the complex conjugate of the wavefunction for the positive energy state. If we take the complex conjugate of the Klein-Gordon equation in an electromagnetic field, we find that
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{c^2}[i\hbar \frac{\partial }{\partial t} + e\phi ]^2 \psi ^{*} (\bold{r} ,t) = ([\frac{\hbar }{i}\bold{\nabla } + \frac{e}{c} \bold{A}]^2 + m^2 c^2 ) \psi ^{*} (\bold{r},t)}
This tells us that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi ^{*} (\bold{r} , t)} is a wavefunction satisfying the Klein-Gordon equation for a particle of mass m and charge -e, which is the antiparticle of a particle of mass m and charge e with wavefunction Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi (\bold{r} , t)} .
Now, the density and current in a frame K' moving with velocity Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -\bold{v}} relative to frame K for the particles will be Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho (\bold{r \prime}, t\prime) = \frac{E_p}{mc^2 }} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bold{j} (\bold{r \prime}, t\prime) = \frac{\bold{p}}{m}} and for the antiparticles the density and current will be Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho (\bold{r \prime}, t\prime) = \frac{-E_p}{mc^2 }} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bold{j} (\bold{r \prime}, t\prime) = \frac{-\bold{p}}{m}} , where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_p = \frac{mc^2 }{\sqrt{1-v^2 / c^2 }}} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bold{p} = \frac{m\bold{v}}{\sqrt{1-v^2 / c^2 }}} .
This tells us that an antiparticle moving in one direction has a current moving in the opposite direction. Thus, a particle current in one direction is equivalent to an antiparticle current in the opposite direction. This applies for propagation through time, as well: a negative energy solution describes equivalently a particle traveling backward in time and an antiparticle traveling forward in time. For charged particles, this is easy to reconcile since the charge of the particle and its antiparticle are opposite; thus, we expect the charge density and current to be opposite.
For neutrally charged particles, however, the difference between particle and antiparticle are a bit more subtle. By observation, we see that there are a few possibilities. First, the particle and its antiparticle may have a "charge" that is not electromagnetic, e.g. the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle{K^0}} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \overline{K^0}} , which have a strangeness of 1 and -1, respectively. It may also be the case that the neutral particle is in fact its own antiparticle, as with the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \pi ^0} , in which case the wavefunction is always real, thus making the current and density zero.
Klein-Gordon equation with Coulomb potential
The Coulomb potential is exactly solvable in the Klein-Gordon equation. The potential four-vector of the Coulomb potential is
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi ^{\mu} = ( \frac{-Ze}{r} ; 0 )}
which makes the Klein-Gordon equation
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [i\hbar \frac{\partial}{\partial t} + \frac{Ze^2}{r}]^2 \psi = -\hbar ^2 c^2 \nabla ^2 \psi + m^2 c^4 \psi}
Let Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi (\bold{r} , t) = R(\bold{r})Y_{\ell m}(\theta , \phi )e^{-\frac{i}{\hbar}Et}}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Rightarrow [-\frac{1}{r^2}\frac{\partial}{\partial r} (r^2 \frac{\partial}{\partial r} ) + \frac{\ell (\ell +1)}{r^2}]R(\bold{r}) = \frac{(E+\frac{Ze^2}{r})^2 - m^2 c^4 }{\hbar ^2 c^2} R(\bold{r})}
Now, letting Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \gamma = \frac{Ze^2}{\hbar c}} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha ^2 = \frac{4(m^2 c^4 - E^2 )}{\hbar ^2 c^2}} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda = \frac{2E\gamma}{\hbar c \alpha}} , and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle{\rho = \alpha r}} ,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Rightarrow (\frac{1}{\rho ^2}\frac{\partial}{\partial \rho}(\rho ^2 \frac{\partial}{\partial \rho}) + [\frac{\lambda}{\rho} - \frac{1}{4} - \frac{\ell (\ell +1) -\gamma ^2}{\rho ^2}])R(\bold{r}) = 0}
Now, let's suppose that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle{R=f(\rho )g(\rho )v(\rho )}} , where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle{f(\rho )}} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle{g(\rho )}} are the asymptotically dominant properties of R at small and large .
As , the term dominates, and , where .
As , the term dominates, and .
Now suppose that . Putting this solution of R into the radial equation and simplifying, we find that follows a recursive relation implying that where N is a constant, and that . Thus,
and
where . If we expand the root in #9.5.2, we find
, where , as in the non-relativistic case.
![{\displaystyle E_{n}=mc^{2}[1-{\frac {\gamma ^{2}}{2n^{2}}}-{\frac {\gamma ^{4}}{2n^{4}}}({\frac {n}{\ell +{\frac {1}{2}}}}-{\frac {3}{4}})+...]=mc^{2}-{\frac {Ry}{n^{2}}}-{\frac {\gamma ^{4}mc^{2}}{2n^{4}}}({\frac {n}{\ell +{\frac {1}{2}}}}-{\frac {3}{4}})+...}](https://wikimedia.org/api/rest_v1/media/math/render/svg/98cfe0ddcfa9f9019ad7a853b7ffd8c59648036e)
Analyzing the energy states, we see that the first term is the rest mass energy of the particle, the second term is the non-relativistic energy levels of the Coulomb potential, and the third term is the fine structure correction. It should be noted that the Klein-Gordon equation is not compatible with spin. As should be observed, the fine structure correction to a particle with spin in a Coulomb potential is , where j is the total angular momentum. The reason we can never reach this correction from the Klein-Gordon equation is because spin has no equivalent four-vector, and so will not couple completely to the Klein-Gordon equation. In order to accommodate spin in any potential, we must use something else. For spin-1/2, that something else is the Dirac equation.
