Phy5670/JahnTellerEffect

Introduction

The Jahn-Teller effect (JTE), also called Jahn Teller distortion, is the spontaneous geometrical distortion of a nonlinear molecule to lower the overall energy of the system by breaking the degeneracy of a ground or excited state, and is the result of coupling between electrons and atomic nuclei. It was shown by Hermann Jahn and Edward Teller in 1937 that the orbital degeneracy of the electronic state in a polyatomic molecule cannot be stable unless the molecule is linear.

Jahn and Teller applied group theory to the perturbation calculation and examined the elements of the perturbation matrix. They showed that all the linear matrix elements vanish only if the molecule has complete axial symmetry (meaning the molecule is linear), and deduced that ``all non-linear nuclear configurations are therefore unstable for an orbitally degenerate electronic state [1]. By this reasoning it is possible to conclude that a polyatomic molecule that is not linear does not possess orbital degeneracy of the electronic ground state. Even molecules that do not have a strict degeneracy, but merely very closely spaced energy levels exhibit Jahn-Teller distortion. This effect in nearly degenerate molecules has been named the pseudo Jahn-Teller effect (PJTE).

The Jahn-Teller effect is of interest in systems with a large number of interacting electrons and nucleui, which constitues a many body problem. It cannot be solved analytically and is beyond the practicality of using a computer. Therefore, as with most many body problems, approximations must be made. The application of the adiabatic approximation, which allows separation of variables based on the difference in masses of electrons and nuclei, led to a more comprehensive understanding of the Jahn-Teller effect. In the formulation of the adiabatic approximation, the Jahn-Teller effect can be written as follows: ``if the adiabatic potential of the system, which is the formal solution of the electronic part of the Schrodinger equation, has several crossing sheets, then at least one of these sheets has no extremum at the crossing point [2]. Further application of the solution of the nuclear part specifies the expected behavior of the nuceli. It is the \textit{combined} solutions of the electronic and nuclear parts of the Schrodinger equation that allow one to predict the behavior of the nuclei. Before this was well understood, many scientists were unable to detect Jahn-Teller distortion in systems they suspected should exhibit the effect.

Magnetic resonance techniques can be used to study the Jahn-Teller effect as a result of the highly sensitive magnetic nuclei present in these systems. The method for observing Jahn-Teller distortion that will be elaborated upon in this wiki is electron paramagnetic resonance (EPR), aka electron spin resonance (ESR). Other magnetic resonance methods that can be used to observer the JTE include nuclear magnetic resonance, acoustic paramagnetic resonance, paraelectic resonance, and Mossbaauer spectroscopy (nuclear gamma resonance) [3].

The Born-Oppenheimer Approximation

The Born-Oppenheimer approximation is often the preferred perturbative method in which to describe the JTE. The Born-Oppenheimer approximation, which is similar in some respects to the adiabatic approximation, is based on the largest contribution to a molecular spectra arising from the electronic motion, followed by the contribution of nuclear vibration, followed by nuclear rotation [4]. These three terms appear in increasing order with respect to $\left({\frac {m}{M}}\right)^{1/4}$, where $m$ is the electronic mass and $M$ is the average nuclear mass. Nuclear vibrations corresponds to second order, while nuclear rotational motion corresponds to fourth order in $\left({\frac {m}{M}}\right)^{1/4}$ [4]. (The electronic motion is zeroth order in $\left({\frac {m}{M}}\right)^{1/4}$.)

In the BO approximation, the nuclei of atoms are assumed to be fixed in space, and therefore their kinetic energy can be neglected. Schrodinger's equation for the electrons is solved - while still including the Coulomb potential resulting from the interaction between the electrons and nuclei. This problem is solved repeatedly for very small changes in position, resulting in an expression for the electronic energy as a function of nuclei position. This is called the potential energy surface. The nuclear kinetic energy is the reintroduced to the Hamiltonian, and Schrodinger's equation is solved again, this time yielding the total energy of the molecule.

For the remained of this section I will define $\kappa =\left({\frac {m}{M}}\right)^{1/4}$, $r_{l}$ is the local nuclear coordinate (where r can be x,y,z), $q_{k}$ is the electron coordinate (where q can be x,y,z). A subscript $e$ denotes an electronic quantity. A subscript $n$ denotes a nuclear quantity.

The total potential energy of the system is

$\sum _{q}\sum _{r}U\left(q_{1},q_{2},q_{3}...;r_{1},r_{2},r_{3},...\right)=U(Q,R)$

where Q encompasses all electronic coordinates, and R encompasses all nuclear coordinates, and the sum on $q$ and the sum on $r$ represent the permutation of x,y,z.

The electronic kinetic energy is

$T_{e}=-{\frac {\hbar ^{2}}{2m}}\sum _{q}\sum _{k}{\frac {\partial ^{2}}{\partial q_{k}^{2}}}$

The nuclear kinetic energy is

$T_{n}=-\kappa ^{4}{\frac {\hbar ^{2}}{2m}}\sum _{r}\sum _{l}\mu _{l}{\frac {\partial ^{2}}{\partial r_{l}^{2}}}$

where $\mu _{l}$ is a dimensionless number on order 1 [4].

The Hamiltonian for a system of electrons and nuclei is given by:

$H=T_{e}+T_{n}+V\left(Q\right)+V(R,Q)$

where the potential has been broken into a part that relies only on the electron coordinates, and a part that includes the electron-nucleus interaction. Using the Born-Oppenheimer approximation we can write a pair of equations:

$\left[T_{e}+V(R,Q)\right]\phi _{e}(R,Q)=W_{e}(Q)\phi _{e}(R,Q)$

$\left[T_{n}+W_{e}(Q)+V(Q)\right]\chi _{n}(Q)=E_{e}\chi _{n}(Q)$

where $\phi _{e}(R,Q)$ is the electronic wave function (Q appears only as a constant in this particular equation), $\chi _{n}(Q)$ is the nuclear wave function, and $W_{e}+V$ is the effective potential as seen by each electronic state [5].

When the electronic states are non-degenerate, the Born-Oppenheimer wave-function are the solutions to the following Hamiltonian, where $\Delta H$ (the second line) is treated as a perturbation [5]:

$H=H_{0}+\Delta H=\left(T_{e}+T_{n}+V(R,Q^{0})+V(Q)+W_{e}(Q)-W_{e}(Q^{0})\right)+\left(V(R,Q)-V(R,Q^{0})-W_{e}(Q)+W_{e}(Q^{0})\right)$

with zero order solutions[5]:

$\psi _{e,n}=\phi _{e}\left(R,Q\right)\chi _{n}(Q)$

When there are degenerate electronic states, the Born-Oppenheimer wave-function are the solutions to the following Hamiltonian [5]:

$H=H_{0}+\Delta H=\left(T_{e}+T_{n}+V(R,Q^{0})+V(Q^{0})+\sum _{e}\left({\frac {W_{e}(Q)-W_{e}(Q^{0})}{[\Gamma ]}}\right)\right)+\left(V(R,Q)-V(R,Q^{0})-\sum _{e}\left({\frac {W_{e}(Q)-W_{e}(Q^{0})}{[\Gamma ]}}\right)\right)$

where $[\Gamma ]$ represents the dimensionality of the degeneracy, and the sum is over all degenerate states. The zero order solutions are given by[5]:

$\psi _{\{e\},n}=\sum _{e}\phi _{e}\left(R,Q\right)\chi _{e,n}(Q)$

Pseudo Jahn-Teller and Renner-Teller Effect

The Pseudo Jahn-Teller effect is the vibronic coupling between a degenerate and a non-degenerate state which is induced by a degenerate mode.

The Renner-Teller effect was first observed in 1959 by K. Dressler and D.A. Ramsay [7] in NH_2 and ND_2.

An Example of Jahn-Teller Distortion

The molecule CuF$_{2}$(H$_{2}$O)$_{2}$(pyz)(pyz = pyrazine) exhibits Jahn-Teller distortion. The CuF$_{2}$(H$_{2}$O)$_{2}$(pyz) is made of pyrazine-bridged CuF$_{2}$O$_{2}$N$_{2}$ octahedra. It exhibits Jahn-Teller distortion in the elongation of Cu-N bonds at ambient conditions. See reference [8] for additional information about the synthesis and characterization of this molecule. See reference [9] for additional information on pressure induced switching of the Jahn-Teller axes.

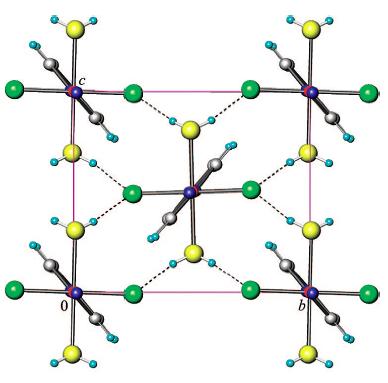
The structure and arrangement of CuF$_{2}$(H$_{2}$O)$_{2}$(pyz) molecules, from reference [8].

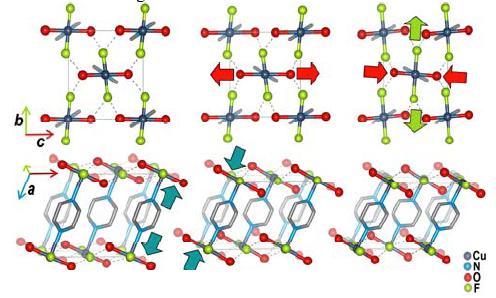
The pressure induced switching of the Jahn-Teller Axes, from reference [9].

References

[1] H.A. Jahn and E. Teller. Proc. Roy. Soc. A, 161, 220 (1937)

[2] I.B. Bersuker and V.Z. Polinger, Vibronic Interactions in Molecules and Crystals Springer-Verlag, 1989.

[3] I.B. Bersuker, The Jahn-Teller Effect A Bibliographic Review, IFI/Plenum Data Company, 1984.

[4] M. Born and R. J. Oppenheimer, Ann. Physik (Leipzig) 89, 457 (1927)

[5] R. Englman, The Jahn-Teller Effect in Molecules and Crystals John Wiley and Sons, 1972

[6] R. Renner, Z. Physik, 92, 172 (1934)

[7] Phil. Trans. Roy. Soc. London, 251A, 553 (1959)]

[8] Jamie L. Manson, et el. Chem. Mater., 2008, 20 (24) 7408-7416

[9] Halder, G. J., Chapman, K. W., Schlueter, J. A. and Manson, J. L. , Pressure-Induced Sequential Orbital Reorientation in a Magnetic Framework Material. Angewandte Chemie International Edition, n/a. doi: 10.1002/anie.201003380