Phy5670/JahnTellerEffect: Difference between revisions
| Line 14: | Line 14: | ||
The Born-Oppenheimer approximation begins with the assumption that the nuclei are fixed at their equilibrium position (i.e. ideal lattice points). A static interaction between the electrons and nuclei must be added to compensate for the actual instantaneous position of the nuclei [5]. The nuclear motion is then solved for, yielding an effective potential which is used in the determination of the electronic motion. | The Born-Oppenheimer approximation begins with the assumption that the nuclei are fixed at their equilibrium position (i.e. ideal lattice points). A static interaction between the electrons and nuclei must be added to compensate for the actual instantaneous position of the nuclei [5]. The nuclear motion is then solved for, yielding an effective potential which is used in the determination of the electronic motion. | ||
The Born-Oppenheimer and adiabatic approximations both rely on the assumption that the mass of the electron (m) is much less than the mass of the nucleus (M). It is interesting to derive some relations between this quantity, <math>\frac{m}{M} </math>, and the velocity of the nucleus, the displacement of the nucleus from equilibrium, and the average energy. These relations can be used to justify the validity of certain steps in the upcoming approximations. | |||
The uncertainty principle along with the expression for the average momentum allows us to write the average velocity of the electron in terms of <math> \hbar </math>, d, and m. In what follows, p is the average momentum of the electrons, v and V are the average velocity of the electrons and nuclei, respectively, <math>Q_0 </math> is the equilibrium point of the nuclei, Q is the displacement from the equilibrium point, and <math>\omega </math> is the frequency of vibration of the nuclei. | |||
<math>\vec{p} \sim \frac{\hbar}{\vec{d}} </math> | |||
<math>\vec{p} = m\vec{v} </math> | |||
<math> \vec{v} \sim \frac{\hbar}{m\vec{d}} </math> | |||
Now examine the nucleus. The kinetic energy and the potential energy of the nucleus can be related through the virial theorem. | |||
<math> \frac{1}{2} M V^2 \sim \frac{1}{2}M\omega^2 Q^2 \sim \hbar\omega </math> | |||
<math> V \sim \left(\frac{\hbar \omega}{M}\right)^2 </math> | |||
<math> Q \sim \left(\frac{\hbar}{M \omega}\right)^2 </math> | |||
We can find an expression for the frequency of vibration, <math>\omega </math>, by relating the force constant resulting from the displacement of the nucleus from its equilibrium positon to the Coulomb's interaction resulting from a given electronic distribution. | |||
<math> M\omega^2 \sim \frac{e^2}{d^3} </math> | |||
The virial theorem relates the potential energy of the electron to the kinetic energy of the electron, which can be substituted into the above equation to yield an expression for the frequency of vibration. | |||
<math> \frac{e^2}{d} \sim m v^2 \sim m\left(\frac{\hbar}{m\vec{d}}\right)^2</math> | |||
<math>M\omega^2 \sim \frac{\hbar^2}{md^4}</math> | |||
<math>\omega^2 \sim \frac{\hbar^2}{m^2d^4}\frac{m}{M} \rightarrow \omega \sim \frac{\hbar}{md^2}\left(\frac{m}{M}\right) </math> | |||
These results can be put back into the expressions for <math> Q </math> and <math> V </math>. | |||
<math> V \sim v\left(\frac{m}{M}\right)^{3/4} </math> | |||
<math> Q \sim d\left(\frac{m}{M}\right)^{1/4} </math> | |||
Thus we have found the dependence of <math> Q </math> and <math> V </math> on the small quantity <math> \frac{m}{M} </math>. | |||
Similarly, we can use the uncertainty relation between energy and time to estimate characteristic energy gap of the electron energy spectrum, <math> \overline{\Delta E} </math>: | |||
<math>\overline{\Delta E} \sim \frac{\hbar}{\overline{\Delta t}} </math> | |||
<math>\overline{\Delta t} \sim \frac{d}{\vec{v}} \sim \frac{m d^2}{\hbar} </math> | |||
<math>\overline{\Delta E} \sim \frac{\hbar^2}{md^2} </math> | |||
<math>\frac{\hbar}{md^2} \sim \left(\frac{M}{m}\right)^{1/2}\omega</math> | |||
<math>\frac{\hbar\omega}{\overline{\Delta E}} \sim \left(\frac{m}{M}\right)^{1/2}</math> | |||
This relation will justify the validity of the adiabatic approximation. | |||
===The Adiabatic Approximation=== | ===The Adiabatic Approximation=== | ||
Revision as of 14:34, 18 November 2010
Introduction
The Jahn-Teller effect (JTE), also called Jahn Teller distortion, is the spontaneous geometrical distortion of a nonlinear molecule to lower the overall energy of the system by breaking the degeneracy of a ground or excited state, and is the result of coupling between electrons and atomic nuclei. It was shown by Hermann Jahn and Edward Teller in 1937 that the orbital degeneracy of the electronic state in a polyatomic molecule cannot be stable unless the molecule is linear.
Jahn and Teller applied group theory to the perturbation calculation and examined the elements of the perturbation matrix. They showed that all the linear matrix elements vanish only if the molecule has complete axial symmetry (meaning the molecule is linear), and deduced that "all non-linear nuclear configurations are therefore unstable for an orbitally degenerate electronic state" [1]. By this reasoning it is possible to conclude that a polyatomic molecule that is not linear does not possess orbital degeneracy of the electronic ground state. Even molecules that do not have a strict degeneracy, but merely very closely spaced energy levels exhibit Jahn-Teller distortion. This effect in nearly degenerate molecules has been named the pseudo Jahn-Teller effect (PJTE).
The Jahn-Teller effect is of interest in systems with a large number of interacting electrons and nucleui, which constitues a many body problem. It cannot be solved analytically and is beyond the practicality of using a computer. Therefore, as with most many body problems, approximations must be made. The application of the adiabatic approximation, which allows separation of variables based on the difference in masses of electrons and nuclei, led to a more comprehensive understanding of the Jahn-Teller effect. In the formulation of the adiabatic approximation, the Jahn-Teller effect can be written as follows: "if the adiabatic potential of the system, which is the formal solution of the electronic part of the Schrodinger equation, has several crossing sheets, then at least one of these sheets has no extremum at the crossing point" [2]. Further application of the solution of the nuclear part specifies the expected behavior of the nuceli. It is the combined solutions of the electronic and nuclear parts of the Schrodinger equation that allow one to predict the behavior of the nuclei. Before this was well understood, many scientists were unable to detect Jahn-Teller distortion in systems they suspected should exhibit the effect.
Magnetic resonance techniques can be used to study the Jahn-Teller effect as a result of the highly sensitive magnetic nuclei present in these systems. The method for observing Jahn-Teller distortion that will be elaborated upon in this wiki is electron paramagnetic resonance (EPR), aka electron spin resonance (ESR). Other magnetic resonance methods that can be used to observer the JTE include nuclear magnetic resonance, acoustic paramagnetic resonance, paraelectic resonance, and Mossbaauer spectroscopy (nuclear gamma resonance) [3].
Approximations and the Vibronic Interaction
There are two approximations that can be used to treat the interactions between the electrons and the nuclei in a many-body system. These two methods are the adiabatic approximation, and the Born-Oppenheimer Approximation (sometimes referred to as the crude adiabatic approximation).
The adiabatic approximation is based on the significantly different electron masses and nuclear masses, which allows us to assume that the nuclei move much more slowly than the electrons. As a result, the distribution of the electrons can be determined from an instantaneous configuration of the nuclei. We assume the nuclei are fixed at some instantaneous (not necessarily equilibrium) position and perform a separation of translational and rotational variables.
The Born-Oppenheimer approximation begins with the assumption that the nuclei are fixed at their equilibrium position (i.e. ideal lattice points). A static interaction between the electrons and nuclei must be added to compensate for the actual instantaneous position of the nuclei [5]. The nuclear motion is then solved for, yielding an effective potential which is used in the determination of the electronic motion.
The Born-Oppenheimer and adiabatic approximations both rely on the assumption that the mass of the electron (m) is much less than the mass of the nucleus (M). It is interesting to derive some relations between this quantity, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{m}{M} } , and the velocity of the nucleus, the displacement of the nucleus from equilibrium, and the average energy. These relations can be used to justify the validity of certain steps in the upcoming approximations.
The uncertainty principle along with the expression for the average momentum allows us to write the average velocity of the electron in terms of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hbar } , d, and m. In what follows, p is the average momentum of the electrons, v and V are the average velocity of the electrons and nuclei, respectively, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Q_0 } is the equilibrium point of the nuclei, Q is the displacement from the equilibrium point, and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega } is the frequency of vibration of the nuclei.
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{p} \sim \frac{\hbar}{\vec{d}} }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{p} = m\vec{v} }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{v} \sim \frac{\hbar}{m\vec{d}} }
Now examine the nucleus. The kinetic energy and the potential energy of the nucleus can be related through the virial theorem.
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{2} M V^2 \sim \frac{1}{2}M\omega^2 Q^2 \sim \hbar\omega }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V \sim \left(\frac{\hbar \omega}{M}\right)^2 }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Q \sim \left(\frac{\hbar}{M \omega}\right)^2 }
We can find an expression for the frequency of vibration, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega } , by relating the force constant resulting from the displacement of the nucleus from its equilibrium positon to the Coulomb's interaction resulting from a given electronic distribution.
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle M\omega^2 \sim \frac{e^2}{d^3} }
The virial theorem relates the potential energy of the electron to the kinetic energy of the electron, which can be substituted into the above equation to yield an expression for the frequency of vibration.
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{e^2}{d} \sim m v^2 \sim m\left(\frac{\hbar}{m\vec{d}}\right)^2}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle M\omega^2 \sim \frac{\hbar^2}{md^4}}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega^2 \sim \frac{\hbar^2}{m^2d^4}\frac{m}{M} \rightarrow \omega \sim \frac{\hbar}{md^2}\left(\frac{m}{M}\right) }
These results can be put back into the expressions for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Q } and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V } .
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V \sim v\left(\frac{m}{M}\right)^{3/4} }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Q \sim d\left(\frac{m}{M}\right)^{1/4} }
Thus we have found the dependence of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Q } and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V } on the small quantity Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{m}{M} } .
Similarly, we can use the uncertainty relation between energy and time to estimate characteristic energy gap of the electron energy spectrum, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \overline{\Delta E} } :
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \overline{\Delta E} \sim \frac{\hbar}{\overline{\Delta t}} }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \overline{\Delta t} \sim \frac{d}{\vec{v}} \sim \frac{m d^2}{\hbar} }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \overline{\Delta E} \sim \frac{\hbar^2}{md^2} }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\hbar}{md^2} \sim \left(\frac{M}{m}\right)^{1/2}\omega}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\hbar\omega}{\overline{\Delta E}} \sim \left(\frac{m}{M}\right)^{1/2}}
This relation will justify the validity of the adiabatic approximation.
The Adiabatic Approximation
The Born-Oppenheimer Approximation
The Born-Oppenheimer approximation is often the preferred perturbative method in which to describe the JTE. The Born-Oppenheimer approximation, which is similar in some respects to the adiabatic approximation, is based on the largest contribution to a molecular spectra arising from the electronic motion, followed by the contribution of nuclear vibration, followed by nuclear rotation [4]. These three terms appear in increasing order with respect to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(\frac{m}{M}\right)^{1/4}} , where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m} is the electronic mass and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle M} is the average nuclear mass. Nuclear vibrations corresponds to second order, while nuclear rotational motion corresponds to fourth order in Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(\frac{m}{M}\right)^{1/4}} [4]. (The electronic motion is zeroth order in Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(\frac{m}{M}\right)^{1/4}} .)
In the BO approximation, the nuclei of atoms are assumed to be fixed in space, and therefore their kinetic energy can be neglected. Schrodinger's equation for the electrons is solved - while still including the Coulomb potential resulting from the interaction between the electrons and nuclei. This problem is solved repeatedly for very small changes in position, resulting in an expression for the electronic energy as a function of nuclei position. This is called the potential energy surface. The nuclear kinetic energy is the reintroduced to the Hamiltonian, and Schrodinger's equation is solved again, this time yielding the total energy of the molecule.
For the remained of this section I will define Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \kappa = \left(\frac{m}{M}\right)^{1/4}} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r_l} is the local nuclear coordinate (where r can be x,y,z), Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle q_k} is the electron coordinate (where q can be x,y,z). A subscript Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e} denotes an electronic quantity. A subscript Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n} denotes a nuclear quantity.
The total potential energy of the system is
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_q \sum_r U\left(q_1, q_2, q_3 ... ; r_1, r_2, r_3, ... \right) = U(Q, R)}
where Q encompasses all electronic coordinates, and R encompasses all nuclear coordinates, and the sum on Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle q} and the sum on Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r} represent the permutation of x,y,z.
The electronic kinetic energy is
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_e = -\frac{\hbar^2}{2m}\sum_q\sum_k \frac{\partial^2}{\partial q_k^2}}
The nuclear kinetic energy is
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_n = -\kappa^4 \frac{ \hbar^2}{2m} \sum_r\sum_l \mu_l \frac{\partial^2}{\partial r_l^2}}
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu_l} is a dimensionless number on order 1 [4].
The Hamiltonian for a system of electrons and nuclei is given by:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H = T_e + T_n + V\left(Q\right) + V(R,Q)}
where the potential has been broken into a part that relies only on the electron coordinates, and a part that includes the electron-nucleus interaction. Using the Born-Oppenheimer approximation we can write a pair of equations:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left[T_e + V(R,Q) \right]\phi_e(R,Q) = W_e(Q)\phi_e(R,Q) }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left[T_n + W_e(Q) + V(Q) \right]\chi_n(Q) = E_e\chi_n(Q)}
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi_e(R,Q)} is the electronic wave function (Q appears only as a constant in this particular equation), Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \chi_n(Q)} is the nuclear wave function, and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle W_e + V} is the effective potential as seen by each electronic state [5].
When the electronic states are non-degenerate, the Born-Oppenheimer wave-function are the solutions to the following Hamiltonian, where (the second line) is treated as a perturbation [5]:
with zero order solutions[5]:
When there are degenerate electronic states, the Born-Oppenheimer wave-function are the solutions to the following Hamiltonian [5]:
where represents the dimensionality of the degeneracy, and the sum is over all degenerate states. The zero order solutions are given by[5]:
Solution To The Jahn-Teller Problem for an Idealized System
Pseudo Jahn-Teller and Renner-Teller Effect
The Pseudo Jahn-Teller effect is the vibronic coupling between a degenerate and a non-degenerate state which is induced by a degenerate mode.
The Renner-Teller effect was first observed in 1959 by K. Dressler and D.A. Ramsay [7] in NH_2 and ND_2.
Observing Jahn-Teller Distortion Through EPR
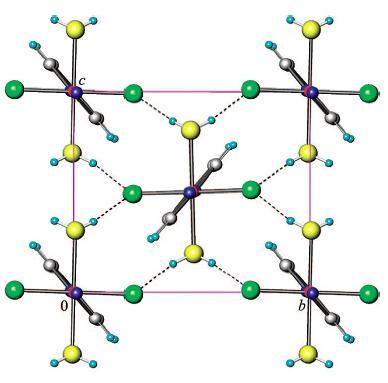
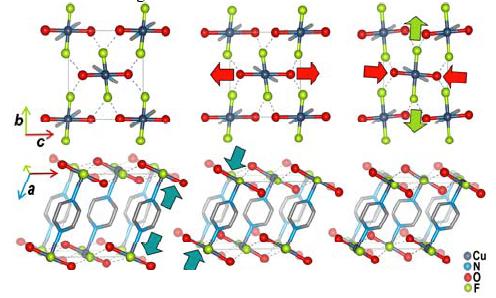
The molecule CuF(HO)(pyz)(pyz = pyrazine) exhibits Jahn-Teller distortion. The CuF(HO)(pyz) is made of pyrazine-bridged CuFON octahedra. It exhibits Jahn-Teller distortion in the elongation of Cu-N bonds at ambient conditions. See reference [8] for additional information about the synthesis and characterization of this molecule. See reference [9] for additional information on pressure induced switching of the Jahn-Teller axes.
The structure and arrangement of CuF(HO)(pyz) molecules, from reference [8].
The pressure induced switching of the Jahn-Teller Axes, from reference [9].
References
[1] H.A. Jahn and E. Teller. Proc. Roy. Soc. A, 161, 220 (1937)
[2] I.B. Bersuker and V.Z. Polinger, Vibronic Interactions in Molecules and Crystals Springer-Verlag, 1989.
[3] I.B. Bersuker, The Jahn-Teller Effect A Bibliographic Review, IFI/Plenum Data Company, 1984.
[4] M. Born and R. J. Oppenheimer, Ann. Physik (Leipzig) 89, 457 (1927)
[5] R. Englman, The Jahn-Teller Effect in Molecules and Crystals John Wiley and Sons, 1972
[6] R. Renner, Z. Physik, 92, 172 (1934)
[7] Phil. Trans. Roy. Soc. London, 251A, 553 (1959)]
[8] Jamie L. Manson, et el. Chem. Mater., 2008, 20 (24) 7408-7416
[9] Halder, G. J., Chapman, K. W., Schlueter, J. A. and Manson, J. L. , Pressure-Induced Sequential Orbital Reorientation in a Magnetic Framework Material. Angewandte Chemie International Edition, n/a. doi: 10.1002/anie.201003380



![{\displaystyle H=H_{0}+\Delta H=\left(T_{e}+T_{n}+V(R,Q^{0})+V(Q^{0})+\sum _{e}\left({\frac {W_{e}(Q)-W_{e}(Q^{0})}{[\Gamma ]}}\right)\right)+\left(V(R,Q)-V(R,Q^{0})-\sum _{e}\left({\frac {W_{e}(Q)-W_{e}(Q^{0})}{[\Gamma ]}}\right)\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d5ca3d2e0c5526d14ff42ad89a7bbea236baeb34)
![{\displaystyle [\Gamma ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2c98e49705831b0a31a81a0e7c3099006bd76ef4)

