Notes 3: Difference between revisions
(New page: == '''Nuclear Astrophysics''' == ---- Nuclear Astrophysics is a multidisciplinary field of modern physics which concerns most notably the studies of Nuclear Physics and Astrophysics. Nu...) |
|||
| (151 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
== '''Nuclear Astrophysics''' == | == '''Nuclear Astrophysics''' == | ||
---- | [[Image:Supernova pathline.jpg|left|125px|thumbnail|Supernova Pathline]] Nuclear Astrophysics is a multidisciplinary field of modern physics which concerns most notably the studies of Nuclear Physics and Astrophysics. Nuclear Astrophysics involves many different branches of physics dealing with the "very small" (Quantum Mechanics, Electrodynamics and Atomic Modeling) to the "very large" (General and Special Relativity, stellar life-cycles and compositions, Galactic formations/constructions and space-time/gravitational effects), and everything in between (such as Statistical/Thermal Mechanics, Kepler Orbits, and Newtonian Mechanics approximations). | ||
Some of the most important subject matters of Nuclear Astrophysics involve element origins and abundances, high energy physics, nuclear reactions and corresponding rates, universal studies (from the Big-Bang model and early universe to the subsequent evolution and expansion of our universe) all the way to structural and chemical modeling of various astronomical objects such as black holes, neutron stars, pulsars, stars, nebulae and supernovae. | |||
Nuclear Astrophysics is perhaps one of the most comprehensive and involved branches of modern physics in that it deals with the widest variety of sub-fields within the discipline. | |||
==Atomic Structure== | |||
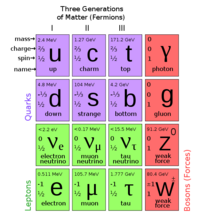
[[Image:Standard Model Of Elementary Particles.png|right|200px|thumbnail|The Standard Model of Elementary Particles]] | |||
Atoms are the basic units of matter, and are comprised of electrons, protons, and neutrons. The protons and neutrons are the densest part of the atom, and located in the nucleus. Electrons orbit this nucleus in quantized energy levels. | |||
=== Electron === | |||
An electron is a subatomic particle with negative charge that orbits the nucleus in an atom. The electron is classified as a lepton. It interacts through the gravitational, electromagnetic, and weak forces. | |||
=== Nucleus === | |||
The nucleus constituents protons and neutrons. The atomic nucleus can be denoted by <math> _Z^A X_N</math>, where <math>Z</math> denotes the number of protons in the nucleus or atomic number, <math>N</math> denotes the number of neutrons, <math>A</math> denotes the number of nucleons or mass number, and <math>X</math> denotes the element symbol. | |||
| Line 12: | Line 17: | ||
One of the most important aspects of Nuclear Astrophysics is being able to calculate elemental abundances in astronomical structures. Particle abundances are given by: | One of the most important aspects of Nuclear Astrophysics is being able to calculate elemental abundances in astronomical structures. Particle abundances are given by: | ||
<math> | |||
Where the | <math>X_i= \frac{n_i}{\Sigma_j {n_j}}</math> | ||
Where the mass fraction <math>X_i</math> is the fraction of total mass of a sample that is made up by a nucleus of species "i". | |||
<math>n_i= \frac{X_i \times \rho }{m_i}</math> | |||
Where <math>{m_i}</math> is the mass of the nucleus of species "i" and rho the corresponding mass density. | |||
== Determination of solar abundances == | |||
=== Earth Material === | |||
Problem: chemical fractionation modified the local composition strongly compared to pre solar nebula and overall solar system. For example, Quarz is 1/3 Si and 2/3 Oxygen and not much else. This is not the composition of the solar system. But, isotopic compositions mostly unaffected (as chemistry is determined by number of electrons (protons), not the number of neurons). | |||
=== Solar Spectra === | |||
Sun formed directly from presolar nebula - (largely) unmodified outer layers create spectral features. | |||
=== Unfractionated meteorites === | |||
Certain classes of meteorites formed from material that never experienced high pressure or temperatures and therefore was never fractionated. These meteorites directly sample the presolar nebula | |||
== Limits of Classical Mechanics == | |||
[[Image:Quantum double slit.jpg|right|200px|thumbnail|An image showing the double slit experiment.]] When dealing with very small or quickly moving objects, the normal, classical laws of physics break down. With the advent of Quantum Mechanics, however, many stellar processes are more easily understood. Quantum Mechanics began to formulate in the early twentieth century, as scientists investigated the composition of atoms, and gained a better understanding of the properties of light. Famous experiments like the double-slit experiment demonstrated a need for a new theory to pick up where classical mechanics broke down. For example, an application of classical physics would predict that an electron would spiral inward towards the nucleus of the atom, whereas quantum theory proposes the Pauli-exclusion principle which dictates discrete energy levels, or steps, that the electron must be contained in. Major players in advancing quantum theory were Niels Bohr, Werner Heisenberg, Max Planck, Louis de Broglie, Albert Einstein, Erwin Schrödinger, Paul Dirac, Wolfgang Pauli, and many, many others. | |||
=== Schrödinger Wave Function === | |||
Hamiltonian Mechanics present the energy of a particle as the sum of it's kinetic and potential energy; | |||
<math>E = T + V = \frac{p^2}{2m} + V</math> | |||
One can apply the following substitutions for p, momentum, and E, energy: | |||
<math>\displaystyle{p \rightarrow \frac{\hbar}{i}\frac{d}{dx}}</math> | |||
<math>\displaystyle{E \rightarrow i\hbar \frac{d}{dt}}</math> | |||
Which results in the following equation for a one-dimensional particle: | |||
<math> i\hbar\frac{\partial}{\partial t}\psi(x,t)=\left[-\frac{\hbar^2}{2m}\frac{\partial^2}{\partial x^2}+V(x,t)\right]\psi(x,t) </math> | |||
== Thermodynamic Quantities/Applications == | |||
When performing calculations on the states and behaviors of particles to approximate much larger astronomical systems, thermal and statistical mechanics may be applied to systems. Particles (in an immediate, and abbreviated manner) fall into the category of either fermions or bosons. Fermions have a spin of 1/2 integer and therefore obey Fermi-Dirac Statistics. Only one fermion can occupy a quantum state at a given time; therefore for two fermions to occupy the same state (i.e. have a degeneracy of 2) they would have to have opposite spins (up or down). Bosons on the other hand obey Bose-Einstein Statistics and possess whole integer spins. Bosons are force-carrying particles while fermions are typically associated with matter constituents. | |||
Many different pertinent quantities may be calculated from these very basic concepts about particles, all of which are very useful in many astrophyical concepts. | |||
'''Particle Density''' | |||
The number of particles per unit volume of any gas can be calculated as such: | |||
<math>n=\frac{N}{V}=\int\omega(p)f(p)dp</math> | |||
where "p" is integrated from <math>0\rightarrow\infty</math> | |||
'''Energy Density''' | |||
The energy per unit volume of any gas can be calculated as such: | |||
<math>u=\frac{U}{V}=\int E\omega(p)f(p)dp</math> | |||
where "p" is again integrated from <math>0\rightarrow\infty</math> | |||
'''Pressure''' | |||
The pressure of any ideal gas is: | |||
<math>P=\frac{1}{3}\int pv\omega(p)f(p)dp</math> | |||
integrated from <math>0\rightarrow\infty</math> | |||
In all three above cases v = velocity of the particles, p = momentum of the particles, E = energy of the state, <math>f(p)</math> = occupation probability of state and <math>\omega(p)</math> = state density per unit volume, N = total number of particles, V = volume of system U = total energy of the system, and g = the degeneracy of the particles. | |||
The number of states for a system of particles can be defined as: | |||
<math>\Phi(E)=\frac{4 \pi g}{3\hbar^{3}}(2m)^{\frac{3}{2}}E^{\frac{3}{2}}</math> | |||
While the state density <math>\omega(p)</math> is defined as: | |||
<math>\omega(E)=(2\pi)\frac{g}{\hbar^{3}}(2m)^{\frac{3}{2}}E^{\frac{1}{2}}</math> | |||
The occupation probabilities of different particles vary based on their different physical interactions/behaviors with each other (such as number of possible particles per state). Therefore because of these derivational differences there are three different occupation probabilities for each statistical distribution. | |||
'''Fermi-Dirac Distribution''' | |||
<math>f(p)=\frac{1}{\exp{(\frac{E(p)-\mu}{kT}})+1}</math> | |||
'''Bose-Einstein Distribution''' | |||
<math>f(p)=\frac{1}{\exp{(\frac{E(p)-\mu}{kT}})-1}</math> | |||
'''Maxwell-Boltzman Distribution''' | |||
<math>f(p)=\exp{(\frac{-(E(p)-\mu)}{kT})}</math> | |||
In the above expressions "<math>\mu</math>" represents the particles' chemical energy, "k" is the Boltzman constant and "T" is the temperature of the gas. | |||
Also, in any of the expressions above, the particles contain energy <math>E=\frac{p^{2}}{2m}</math> where the momentum <math>p=mv</math> can be used interchangeably. | |||
== Basic Nuclear Physics == | |||
All nuclei are formed from combinations of protons and neutrons. These two particles are similar in mass: | |||
'''Mass of Proton: '''<math>m_{p}</math>=938.272 <math>MeV/c^{2}</math> | |||
'''Mass of Neutron: '''<math>m_{n}</math>=939.565 <math>MeV/c^{2}</math> | |||
however, the proton has charge <math>+1e</math> while the neutron is electrically neutral. | |||
These two types of particles interact with each other within the nucleus via two forces, the strong nuclear force and the Coulomb (electromagnetic) force. Since the Coulomb interaction is coupled to charged particles, it only affects protons; both protons and neutrons are sensitive to the strong nuclear force. However, the strong nuclear force is a very short-range force, active at separations of ~ 1 fm. | |||
=== Binding Energy === | |||
The mass of a specific nuclei will be lower than the sum of its constituent particles, and the difference is called the binding energy of the nucleus: | |||
'''Binding Energy:''' <math>B(Z,N)=Zm_{p}+Nm_{n}-M(Z,N)</math> | |||
where <math>m_{p}</math> is the proton mass, <math>m_{n}</math> is the neutron mass, and M(Z,N) is the mass of the nucleus, and Z and N play their usual roles as the proton and neutron number, respectively. | |||
== Main Nuclear Decays Between Driplines == | |||
[[Image:Table of Nuclides.jpg|thumbnail|300px|right|The Table of Nuclides, the Nuclear Physics analogy to the Periodic Table.]] | |||
When dealing with the behavior of an atom, one must consider first the stability of the atom (element). Some atomic arrangements are naturally stable, while others are unstable and quickly (or slowly) decay into other constituents. By changing the proton and neutron numbers of atoms you obtain different isotopes or elements. Only a certain number are stable and do not decay into other, smaller, atoms. | |||
Driplines are the conceptualized boundaries between stable and unstable atoms. When plotted, all the atoms together form the Table of Nuclides; showm below. | |||
The Table of Nuclides is essentially the Nuclear Physics analogy of the Periodic Table of Elements. It summarizes all nuclear arrangements which are observed or calculated as stable, or unstable. | |||
The driplines are the lines bordering the upper and lower boundaries of the main sequence of stable atoms. Around these driplines, the unstable atoms will decay into other atoms, releasing energy. | |||
It is important to understand the characteristics of these types of decay in order to understand the nature of the atoms in question. There are four forces of our universe which govern virtually all of physical nature: Gravitational Force, Electromagnetic Force, Strong Nuclear Force and Weak Nuclear Force. The strong and weak forces are responsible for stong and weak decay interactions. | |||
'''Strong Decays (Short time spans)''' | |||
1. Alpha decay: Alpha Decay refers to when an atom decays via expelling a Helium nucleus from it's own nucleus. The following reaction takes place: | |||
<math>(Z,A)\rightarrow(Z-2,A-4)+^4He</math> where: | |||
<math>M_{nuc}(^4He)+M_{nuc}(Z-2,A-4)\le M_{nuc}(Z,A)</math> and: | |||
<math>M_{at}(^{4}He)+M_{at}(Z-2,A-4)\le M_{at}(Z,A)</math> | |||
2. Fission: Fission refers to the process of the atom decaying (splitting) into essentially two equal pieces (approximately). Under this type of decay, the following reaction takes place: | |||
<math>(Z,A)\rightarrow(\approx\frac{Z}{2},\approx\frac{A}{2})</math> where: | |||
<math>2*M_{nuc}(\frac{Z}{2},\frac{A}{2})\le M_{nuc}(Z,A)</math> and: | |||
<math>2*M_{at}(\frac{Z}{2},\frac{A}{2})\le M_{at}(Z,A)</math> | |||
'''Weak Interactions (Long time spans)''' | |||
3. Beta Decay (<math>\beta^-</math>): This type of decay refers to the type of beta decay where an electon is expelled from the atom along with an accompanying electron antineutrino. This decay is given by the following reaction: | |||
<math>(Z,A)\rightarrow (Z+1,A)+e^{-}+\bar{\nu_e}</math> where: | |||
<math>M_{nuc}(Z,A)\ge M_{nuc}(Z+1,A)+m_e</math> and: | |||
<math>M_{at}(Z,A)\ge M_{at}(Z+1,A)</math> | |||
4. Beta Decay (<math>\beta^+</math>): This type of decay refers to the type of beta decay in which a positron is expelled from the atom along with an electron neutrino as well. This type of decay is given by the following reaction. | |||
<math>(Z,A)\rightarrow (Z-1,A)+e^{+}+\nu_e</math> where: | |||
<math>M_{nuc}(Z,A)\ge M_{nuc}(Z-1,A)+m_e</math> and: | |||
<math>M_{at}(Z,A)\ge M_{at}(Z-1,A)+2*m_e</math> | |||
5. Electron Capture: Electron capture is a different type of decay, in which the atom actually gains an electron and expells a neutrino instead, giving off energy. This is sometimes known as "inverse beta decay", however is often looked at as a type of beta decay regardless. This type of decay is reserved for atoms which are very proton rich and do not have enough energy to expell a positron and a neutrino (typically in environments with very high density and temperatures). The reaction is given by: | |||
<math>(Z,A)+e^-\rightarrow (Z-1,A)+\nu_e</math> where: | |||
<math>M(Z,A)+m_e\ge M(Z-1,A)</math> and: | |||
<math>M_{at}(Z,A)\ge M_{at}(Z-1,A)</math> | |||
=== Role of the Coulomb Barrier in Nuclear Decays === | |||
[[Image:cbarrier.jpg|right|300px|thumbnail|A strong-force/Coulomb barrier superposition nuclear potential, with a prospective tunneling particle.]] | |||
When a nucleus decays, the decay particles must quantum tunnel through the potential barrier created by the nucleus' Coulomb potential. The probability of tunneling is, in the WKB approximation, | |||
<math>T \propto e^{\int_{x_1}^{x_2} {\sqrt{2m(V(x)-E)}}dx}</math>, where <math>x_1</math> and <math>x_2</math> are the radial positions of the Coulomb barrier at the particle's energy level, i.e. <math>(x_2-x_1)</math> is the distance the particle must tunnel. | |||
When the potential is the Coulomb potential, <math>V(x) = \frac {Z_1 Z_2 e^2}{x}</math>, the tunneling probability can be written as | |||
<math>T = e^{2 \pi \eta}</math>, where <math>\eta = \sqrt{\frac {m}{2E}}\frac{Z_1 Z_2 e^2}{\hbar}</math>. The value of <math>\eta</math> is called the '''Sommerfeld parameter.''' Here, <math> Z_1</math> and <math>Z_2</math> are the electric charge of the parent nucleus and the decay particle, and E is the energy of the decay particle. | |||
== Nuclear Cross Sections == | |||
A critical part of understanding nunclear reactions is understanding the cross sections associated with different situations. There are different quantum mechanical potentials unique to certain conditions (such as the Coulomb Potential illustrated above) which change the Hamiltonian of a system, and thus allow differing wavefuctions for their respective regions. Based on the way these wavefunctions should behave, we can calculate the direct Transition Probabilities (i.e. the probability a wave or particle will "tunnel" through a potential barrier) for any general case, as follows: | |||
<math>T=\frac{j_{fin}}{j_{in}}=\frac{k_{fin}\vert\psi_{fin}\vert^2}{k_{in}\vert\psi_{in}\vert^2}</math> | |||
Where the quantum mechanical flux "<math>j</math>" can be defined as the flux of incoming particles (waves) in the reaction: | |||
<math>\vec{j}=\frac{\hbar}{2mi}(\psi^{\ast}\vec{\nabla}\psi-\psi\vec{\nabla}\psi^{\ast})</math> | |||
The "cross section" of a nuclear reaction is essentially a probability that a nuclear reaction will occur at all given the parameters of the nuclei and particles involved. It is effected by many contributing factors; notably the quantum mechanical potential being dealt with and the flux of incoming particles <math>j</math>. It can be defined most generally as: | |||
<math>Cross\ Section=\sigma=\frac{number\ of\ reactions\ per\ target/sec}{flux\ of\ incoming\ projectiles}</math> | |||
However, the cross section for a nuclear reaction can be expressed in terms of a summation over all possible angular momentum values <math>l</math> and the respective transmission coefficients for those <math>l</math> values as follows: | |||
<math>\sigma=\frac{\pi}{k^2}\Sigma(2l+1)T_l</math> | |||
Where the summation above sums all contributing <math>l</math> values for <math>l=0,\ 1,\ 2,...,\infty</math> | |||
It is important to properly describe the wave functions involved in these types of problems as well. Incoming plane waves represent incoming particles and can be defined as: | |||
<math>\psi_{in}=e^{\imath kr}=e^{\imath krcos\theta}=\sqrt{4\pi}\Sigma\sqrt{2l+1}\imath^{l}j_{l}(kr)Y_{l,0}(\theta)</math> | |||
Again, summing over all contributing <math>l</math> values. And the Bessel Functions <math>j_{l}(kr)</math> can be approximated at large <math>kr</math> as: | |||
<math>j_{l}(kr)\rightarrow \frac{\sin(kr-\frac{\pi l}{2})}{kr}</math> | |||
<math>\sin(x)=\frac{\imath}{2}(e^{-\imath x}-e^{\imath x})</math> | |||
Now, we can obtain definitions for our incoming and outgoing wavefunctions: | |||
<math>\psi_{in}=\frac{\sqrt{\pi}}{kr}\Sigma\sqrt{2l+1}\imath^{l+1}(e^{-\imath(kr-\frac{\pi l}{2})}-e^{\imath(kr-\frac{\pi l}{2})})Y_{l,0}</math> | |||
<math>\psi_{trans}=\frac{\sqrt{\pi}}{kr}\Sigma\sqrt{2l+1}\imath^{l+1}(e^{-\imath(kr-\frac{\pi l}{2})}-\eta_{l}e^{\imath(kr-\frac{\pi l}{2})})Y_{l,0}</math> | |||
(Where <math>\eta</math> is described in section above, and summations are, again, over all contribultions of the <math>l</math> components.) | |||
After many derivations from this information we can redefine the cross section as follows (in more succinct form): | |||
<math>\sigma=\frac{-\int\vec{e}_{r}\vec{j}_{t} r^{2} d \Omega}{\vert\vec{j}_{in}\vert}</math> | |||
Therefore, the total cross section for reactions can be described as: | |||
<math>\sigma=\frac{\pi}{k^{2}}\Sigma(2l+1)(1-\vert\eta_{l}\vert^{2})=\frac{\pi}{k^{2}}\Sigma(2l+1)T_{l}</math> | |||
This is exactly as was stated above. However, it should be noted that at low energies (of incoming projectiles), S-waves will dominate because the scattering probability "<math>\eta_{l}</math>" decreases. | |||
== Thermonuclear Reactions == | |||
Understanding thermonuclear reactions is a vital piece of understanding a great number of astrophysical phenomena. The primary goal of understanding the behavior of different thermonuclear reactions essentially boils down to determining the energy and abundance changes of different nuclides involved in a given system. Thermonuclear reactions are most notably referred to (generally) as a nuclear fusion process occurring at very high temperatures in the interiors of stars. | |||
To begin with, before we can explore the deeper workings of thermonuclear reactions, we need to define the rate of nuclear reactions <math>r</math>of a certain species "<math>i</math>" with another species "<math>j</math>": | |||
<math>\sigma=\frac{number\ of\ reactions\ target^{-1}sec^{-1}}{flux\ of\ incoming\ particles}=\frac{r/n_i}{n_jv}</math> | |||
In order to experiment either (theoretically or actually) with thermonuclear reactions, therefore, all one needs to know are the cross sections "<math>\sigma</math>" and the velocity distribution of the beam and the target. | |||
Assuming we are dealing with a non-degenerate Blotzman gas, we can define the reaction rates as: | |||
<math>r_{i,j}=n_in_j\int\sigma(\vert\vec{v}_i-\vec{v}_j\vert)\vert\vec{v}_i-\vec{v}_j\vert\phi(\vec{v}_i)\phi(\vec{v}_j)d^{3}v_{i}d^3v_{j}</math> | |||
Or, more compactly: <math>r_{i,j}=n_{i}n_{j}\langle\sigma v\rangle_{i;j}</math> | |||
Where: <math>\phi(\vec{v}_i)\phi(\vec{v}_j)=\frac{(m_{i}m_{j})^{3/2}}{(2\pi kT)^{3}}exp(-\frac{m_{i}v_{i}^{2}+m_{j}v_{j}^{2}}{2kT})</math> | |||
Now, if we transform this relationship into a center of mass frame using Newton's Laws, we can obtain an expression for <math>\langle\sigma v\rangle</math> and if we know the abundances of each species we can easily calculate their reaction rates: | |||
<math>\langle\sigma v\rangle(T)= (\frac{8}{\mu\pi})^{1/2}\frac{1}{(kT)^{3/2}}\int E\sigma(E)exp(-\frac{E}{kT})dE</math> | |||
Where "<math>E</math>" is integrated from infinity to zero (over all positive values). | |||
Now, from the above equation if we know the energy of a system of particles and can correctly solve it, then we can derive reaction rates for specific types of reactions such as Resonant Reactions (typical at relatively low temperatures), Non-Resonant Reactions for Neutrons (s-waves with l=0) and Non-Resonant Reactions for charged particles. | |||
== The "Big Bang" and Early Universe== | |||
Understanding our universe as it is today requires an understanding of what happened ''before'' today. In order to do this, we are required to maintain certain assumptions about the universe we live in. To begin with, it is a rather obvious assumption that the universe is ''extremely'' large. In addition to being unfathomably huge, and old, we assume that in general the universe is made of the same material as Earth. This can be summed up in the Cosmological Principle: "When averaged over a large enough volume, the universe appears the same in all locations." This speaks to the homogeneity of our universe and is a cornerstone in subsequent calculations. However this principle bears with it many other implications as well; such as the fact that the universe must not have boundaries and that any volume this principle is applied to must be greater than 500Mpc. | |||
'''The Friedman Equation''' is an equation which governs the expansion of an isotropic gas, and is able to be used because we assume the universe is more or less homogeneous on large enough scales. | |||
<math>(\frac{\dot{R}}{R})^{2}=H^{2}(t)=\frac{8 \pi G \rho}{3}-\frac{kc^{2}}{R^{2}}</math> | |||
Above, "<math>R(t)</math>" represents the scale parameter and "<math>k</math>" determines the geometry of the universe. Where here, we have three cases: | |||
<math>k\ge 0 \rightarrow Closed\ Universe\ (Big\ Crunch;\ the\ universe\ eventually\ shrinks\ back\ to\ the\ size\ it\ was\ before\ the\ Big\ Bang)</math> | |||
<math>k=0 \rightarrow Flat\ Universe\ (Universe\ continues\ to\ expand\ at\ a\ constant\ rate\ forever)</math> | |||
<math>k\le 0 \rightarrow Open\ Universe\ (Big\ Chill;\ the\ universe\ expands\ forever\ at\ an\ increasing\ rate)</math> | |||
==Main Sequence Stars== | |||
The Main Sequence contains stars in a distinctive band on the Hertzsprung-Russell diagram, correlating luminosity to temperature. A majority of stars are along the main sequence, which is predictable due to the fact that Main Sequence stars are fusing hydrogen, something stars will spend most of their time doing. | |||
== Hydrostatic Equilibrium and Equations of Stellar Structure == | |||
Hydrostatic Equilibrium in stellar structures is a very important idea because it allows us to approximate/calculate various equations of states of differing types of stars based on the idea that things "are not changing very much". More precisely, a "fluid element" (volume element of gas inside a star) is balanced and essentially held in place by the balancing forces of the inward pull of gravity with the outward force of the gas's pressure gradient. | |||
'''Force of Pressure Gradient:''' | |||
<math>F_{P}=PdA-(P+dP)dA-dPdA</math> | |||
'''Force of Gravity:''' | |||
<math>F_{G}=-GM(r)\rho (r)\frac{dAdr}{r^{2}}</math> | |||
For these two forces to balance we require that: <math>F_{P}=F_{G}</math> | |||
<math>\frac{dP}{dr}=-\frac{GM(r)\rho (r)}{r^{2}}</math> | |||
From these equations we can gather simple estimates for stellar structures and their equations of states: | |||
'''Pressure Equilibrium:''' | |||
<math>\frac{dP_{r}}{dr}=-\frac{GM_{r}\rho_{r}}{r^{2}}</math> | |||
'''Conservation of Mass:''' | |||
<math>\frac{dM_{r}}{dr}=4\pi r^{2} \rho_{r}</math> | |||
It is important to note (however obvious) that the mass of a star (and therefore it's density as well) is not uniformly distributed. The vast majority of the mass is concentrated at a star's center and therefore the star's core is incredibly dense; while the outer regions of a star's interior have very little mass and are therefore not very dense at all. | |||
However, the star looses energy everywhere at it's surface in the form of heat, and more importantly, light. We measure this loss of energy in a star as ''Luminosity''. In fact, in order to keep the temperature constant everywhere, luminosity ''must'' be generated. This generation of energy is comprised of all nuclear processes within the star that generate the star's energy. This rate of energy generation is known as "<math>\epsilon</math>". We approximate the star(s) as a spherical surface, radiating energy at a radius "<math>r</math>". Therefore, the energy equation can be described as (where "<math>L</math>" is the star's Luminosity): | |||
'''Energy Generation Equation:''' | |||
<math>\frac{dL(r)}{dr}=4\pi r^{2}\rho \epsilon</math> | |||
A star's luminosity is generated at it's center, and increases as various nuclear processes carry the energy to the surface of the star at which point the star's luminosity is a constant value. Therefore, the temperature ''inside'' a star must increase as you approach the center in order to allow for energy transportation from the star's center to it's surface. This energy transport (or convection) can be described by the Energy Transport Equation: | |||
'''Energy Transport Equation:''' | |||
<math>\frac{dT_{r}}{dr}=(1-\frac{1}{\gamma})\frac{T_{r}}{P_{r}}\frac{dP_{r}}{dr}=-\frac{3}{32\pi\sigma c}\frac{\kappa \rho L}{r^{2}T^{3}}</math> | |||
== Chain of Reactions/Reaction Rates == | |||
Inside stars (primarily main-sequence stars), the energy necessary to sustain the star derives from various chains of nuclear reactions. In general, these stars begin with consisting primarily of a species <math>Y_{i}</math> (usually Hydrogen) and burn it at a specific rate <math>\frac{dY_{i}}{dt}</math> into another species <math>Y_{i+1}</math>. The species <math>Y_{i+1}</math> is thus burned to create species <math>Y_{i+2}</math> and so on. | |||
When we look at this relationship, we see that the series (chain) of reactions depicts a specific pattern, which deems every species "i" that decays into a species "i+1" depend on the previous state "i". Likewise, the state "i+1" decays into "i+2" and so species "i+1" will also depend on species "i+2" as well. Therefore, if we begin with a species "1", which decays into species "2", and then decays into species "3", the abundance of species "2" can be defined as: | |||
<math>\frac{dY_{2}}{dt}=Y_{1}\lambda_{12}-Y_{2}\lambda_{23}</math> | |||
where: | |||
<math>\lambda_{12}=\frac{1}{1+\delta_{p1}}Y_{p}\rho N_{A}<\sigma \nu >_{1\rightarrow 2}</math> | |||
However, under these circumstances, we must make a couple assumptions regarding these reactions. First of all we assume that in the above example <math>Y_{1}</math> is a constant (essentially, because depletion is very slow due to the bottle neck) and that the capture rates are constant as well. | |||
However, under these assumtions where <math>Y_{1}\approx constant\ and Y_{p} \approx constant</math>, then after some time <math>Y_{2}</math> will reach an equilibrium abundance. Once at equilibrium: | |||
<math>\frac{dY_{2}}{dt}=Y_{1}\lambda_{12}-Y_{2}\lambda_{23}=0</math> and <math>Y_{2}\lambda_{23}=Y_{1}\lambda_{12}</math> | |||
This relationship continues for the remainder of the chain up to "<math>n</math>" species where the abundances times the rates are all equal. This is called "Steady State". | |||
== Neutrino Physics == | |||
Neutrinos are very lightweight (~eV), electrically neutral leptons which are necessary for weak reactions to commence. The lepton number of a system must be conserved, so whenever a beta-plus or beta-minus reaction occurs (<math>\beta^+</math> or <math>\beta^-</math>), a neutrino is required to keep the lepton number constant as well as to conserve linear and angular momentum. | |||
Historically, there were three massless neutrinos, one corresponding to each lepton: the electron neutrino (<math>\nu_e</math>), the muon neutrino (<math>\nu_\mu</math>), and the tau neutrino (<math>\nu_\tau</math>). This understanding produced problems when neutrinos developed by the sun's fusion were measured: only about a third of the expected neutrinos were actually detected by the Homestead Experiment, a late-1960's experiment conducted by Raymond Davis, Jr and John Bahcall. | |||
For the next thirty years, the neutrino deficit was a major unsolved problem in physics. It was only resolved in the early 2000's when it was found by the Sudbury Neutrino Observatory (which was capable of detecting tau and muon neutrinos as well as the expected electron neutrinos) that the neutrinos oscillated in their flavor as they propagated from the core of the sun to the Earth. Current theories of stellar structure and nuclear physics predicted that electron neutrinos from the PP chain reactions occurring in the sun's core would propagate to the Earth, when in fact these electron neutrinos were oscillating in their flavor, becoming tau and muon neutrinos. | |||
== Stellar Burning Cycles == | |||
[[Image:ElemOrigin.jpg|right|300px|thumbnail|The origins of various elements.]] | |||
Stars undergo a variety of different evolutions based on their original chemical composition, mass, density and other traits. Most stars in early burning stages are primarily composed of Hydrogen (the most abundant element in the universe). Through the series of PP (proton-proton) reactions, Hydrogen is fused together to form Helium. Helium is then (once it becomes abundant enough) fused together to make Carbon, Nitrogen, and Oxygen (CNO Cycle). This is the process by which Helium is consumed. | |||
However, stars can undergo a variety of different changes based on their mass. | |||
<math>M(r)> 11M_{\odot}</math>: Matter is not processed | |||
<math>8M_{\odot}< M(r)< 11M_{\odot}</math>: Star undergoes partial Hydrogen burning | |||
<math>6M_{\odot}< M(r)< 8M_{\odot}</math>: Complete Hydrogen burning, but no Helium burning | |||
<math>3.3M_{\odot}< M(r)< 6M_{\odot}</math>: There is incomplete Helium burning; and Carbon-12 is enhanced, while there is no Oxygen-16 produced | |||
<math>M(r)< 3.3M_{\odot}</math>: There is complete Hydrogen burning, then the star moves on to more advanced burning stages | |||
The mass of a star is directly correlated to the burning conditions observed, and the elements the star's burning produces. | |||
== Origin of Heavy Elements == | |||
When discussing the origin of "Heavy Elements", we typically refer to atomic masses heavier than FeI (Iron I). First of all, if we were to plot the universe's abundances of all elements/nuclides as a function of atomic mass number, we would notice that nuclides with mass numbers greater than Fe are far less abundant. These "heavy" atoms are formed from a series of neutron captures and subsequent decays. The process can be broken into two distinct forms of the process: the r-process and the s-process. | |||
[[Image:S-process-elem-Ag-to-Sb.png|200px|thumbnail|right|The characteristic "zig-zag" of the S-process demonstrated in the transition from Ag to Sb.]]'''S-Process:''' Referrs to "slow" neutron capture with respect to decays and weak interactions. The s-process is responsible for approximately half the stable, heavy elements beyond the iron peak and occurrs in stars with low neutron density and [relatively] low temperatures. Heavier elements are formed via the process of capturing a neutron and becoming an unstable isotope of the original element. Under the neutron conditions described above the average time for another neutron capture to occurr is far greater than the average time of a <math>\beta^{-}</math> decay to occurr so the nucleus almost immediately <math>\beta^{-}</math> decays to a heavier, stable element. Therefore the s-process propagates strictly in the valley of stable isotopes and "zig-zags" its way to the top of the table of nuclides diagonally. | |||
'''R-Process''' Referrs to "rapid" neutron capture with respect to deays and weak interaction. It is responsible for roughly the other half of all nuetron-rich atoms in the universe and is most common during core collapse of supernovae. Here, the neutron density is much higher and so neutron capture on stable elements occurrs much more rapidly. Stable "seed" elements are bombarded with rapid neutron captures and extend far into the neutron dripline territory on the table of nuclides. These highly unstable isotopes then subsequently <math>\beta^{-}</math> decay to form stable nuclei. | |||
It is important to note here that both these processes include neutron capture and subsequent decays, however the ''rate'' of neutron capture dictates how the heavier elements are built up. This capture rate is determined by the temperature of the region, and the neutron density. This process would extrapolate forever, except for the fact that once the elements' atomic mass number reaches <math>\approx</math>200, they begin to become very <math>\alpha</math> decay unstable and begin decaying faster than they are created. | |||
Under these processes, the rate equations governing atomic abundances reduces to: | |||
<math>\frac{dN_{A}}{d\tau}=-N_{n}<\sigma v>_{A}N_{A}+N_{n}<\sigma v>_{A-1}N_{A-1}</math> | |||
where: <math>\sigma \approx \frac{1}{v} \sigma_{A}</math> | |||
So, we're left with: | |||
<math>\frac{dN_{A}}{d\tau}=-\sigma_{A}N_{A}+\sigma_{A-1}N_{A-1}</math> | |||
When solving the above rate equation for the abundances of subsequent nuclei, it is important to state that it abides by "Stationarity". That is, given the conditions of the processes, we can essentially state each component is constant. | |||
It is also important to note that niether of these processes would be possible without "seed" nuclei. Seed nuclei are usually the elements Fe (s-process) or Ni (r-process) and serve as the somewhat heavy elements that must be present to begin capturing neutrons in the first place (in abundances of at least 0.04). | |||
Latest revision as of 00:40, 29 April 2011
Nuclear Astrophysics
Nuclear Astrophysics is a multidisciplinary field of modern physics which concerns most notably the studies of Nuclear Physics and Astrophysics. Nuclear Astrophysics involves many different branches of physics dealing with the "very small" (Quantum Mechanics, Electrodynamics and Atomic Modeling) to the "very large" (General and Special Relativity, stellar life-cycles and compositions, Galactic formations/constructions and space-time/gravitational effects), and everything in between (such as Statistical/Thermal Mechanics, Kepler Orbits, and Newtonian Mechanics approximations).
Some of the most important subject matters of Nuclear Astrophysics involve element origins and abundances, high energy physics, nuclear reactions and corresponding rates, universal studies (from the Big-Bang model and early universe to the subsequent evolution and expansion of our universe) all the way to structural and chemical modeling of various astronomical objects such as black holes, neutron stars, pulsars, stars, nebulae and supernovae. Nuclear Astrophysics is perhaps one of the most comprehensive and involved branches of modern physics in that it deals with the widest variety of sub-fields within the discipline.
Atomic Structure
Atoms are the basic units of matter, and are comprised of electrons, protons, and neutrons. The protons and neutrons are the densest part of the atom, and located in the nucleus. Electrons orbit this nucleus in quantized energy levels.
Electron
An electron is a subatomic particle with negative charge that orbits the nucleus in an atom. The electron is classified as a lepton. It interacts through the gravitational, electromagnetic, and weak forces.
Nucleus
The nucleus constituents protons and neutrons. The atomic nucleus can be denoted by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle _Z^A X_N} , where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z} denotes the number of protons in the nucleus or atomic number, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle N} denotes the number of neutrons, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A} denotes the number of nucleons or mass number, and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X} denotes the element symbol.
Particle Abundances
One of the most important aspects of Nuclear Astrophysics is being able to calculate elemental abundances in astronomical structures. Particle abundances are given by:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X_i= \frac{n_i}{\Sigma_j {n_j}}}
Where the mass fraction Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X_i} is the fraction of total mass of a sample that is made up by a nucleus of species "i".
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n_i= \frac{X_i \times \rho }{m_i}}
Where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {m_i}} is the mass of the nucleus of species "i" and rho the corresponding mass density.
Determination of solar abundances
Earth Material
Problem: chemical fractionation modified the local composition strongly compared to pre solar nebula and overall solar system. For example, Quarz is 1/3 Si and 2/3 Oxygen and not much else. This is not the composition of the solar system. But, isotopic compositions mostly unaffected (as chemistry is determined by number of electrons (protons), not the number of neurons).
Solar Spectra
Sun formed directly from presolar nebula - (largely) unmodified outer layers create spectral features.
Unfractionated meteorites
Certain classes of meteorites formed from material that never experienced high pressure or temperatures and therefore was never fractionated. These meteorites directly sample the presolar nebula
Limits of Classical Mechanics
When dealing with very small or quickly moving objects, the normal, classical laws of physics break down. With the advent of Quantum Mechanics, however, many stellar processes are more easily understood. Quantum Mechanics began to formulate in the early twentieth century, as scientists investigated the composition of atoms, and gained a better understanding of the properties of light. Famous experiments like the double-slit experiment demonstrated a need for a new theory to pick up where classical mechanics broke down. For example, an application of classical physics would predict that an electron would spiral inward towards the nucleus of the atom, whereas quantum theory proposes the Pauli-exclusion principle which dictates discrete energy levels, or steps, that the electron must be contained in. Major players in advancing quantum theory were Niels Bohr, Werner Heisenberg, Max Planck, Louis de Broglie, Albert Einstein, Erwin Schrödinger, Paul Dirac, Wolfgang Pauli, and many, many others.
Schrödinger Wave Function
Hamiltonian Mechanics present the energy of a particle as the sum of it's kinetic and potential energy;
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E = T + V = \frac{p^2}{2m} + V}
One can apply the following substitutions for p, momentum, and E, energy:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle{p \rightarrow \frac{\hbar}{i}\frac{d}{dx}}}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle{E \rightarrow i\hbar \frac{d}{dt}}}
Which results in the following equation for a one-dimensional particle:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i\hbar\frac{\partial}{\partial t}\psi(x,t)=\left[-\frac{\hbar^2}{2m}\frac{\partial^2}{\partial x^2}+V(x,t)\right]\psi(x,t) }
Thermodynamic Quantities/Applications
When performing calculations on the states and behaviors of particles to approximate much larger astronomical systems, thermal and statistical mechanics may be applied to systems. Particles (in an immediate, and abbreviated manner) fall into the category of either fermions or bosons. Fermions have a spin of 1/2 integer and therefore obey Fermi-Dirac Statistics. Only one fermion can occupy a quantum state at a given time; therefore for two fermions to occupy the same state (i.e. have a degeneracy of 2) they would have to have opposite spins (up or down). Bosons on the other hand obey Bose-Einstein Statistics and possess whole integer spins. Bosons are force-carrying particles while fermions are typically associated with matter constituents. Many different pertinent quantities may be calculated from these very basic concepts about particles, all of which are very useful in many astrophyical concepts.
Particle Density The number of particles per unit volume of any gas can be calculated as such:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n=\frac{N}{V}=\int\omega(p)f(p)dp} where "p" is integrated from Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0\rightarrow\infty}
Energy Density The energy per unit volume of any gas can be calculated as such:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u=\frac{U}{V}=\int E\omega(p)f(p)dp} where "p" is again integrated from Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0\rightarrow\infty}
Pressure The pressure of any ideal gas is:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P=\frac{1}{3}\int pv\omega(p)f(p)dp} integrated from Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0\rightarrow\infty}
In all three above cases v = velocity of the particles, p = momentum of the particles, E = energy of the state, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(p)} = occupation probability of state and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega(p)} = state density per unit volume, N = total number of particles, V = volume of system U = total energy of the system, and g = the degeneracy of the particles.
The number of states for a system of particles can be defined as:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi(E)=\frac{4 \pi g}{3\hbar^{3}}(2m)^{\frac{3}{2}}E^{\frac{3}{2}}}
While the state density Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega(p)} is defined as:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega(E)=(2\pi)\frac{g}{\hbar^{3}}(2m)^{\frac{3}{2}}E^{\frac{1}{2}}}
The occupation probabilities of different particles vary based on their different physical interactions/behaviors with each other (such as number of possible particles per state). Therefore because of these derivational differences there are three different occupation probabilities for each statistical distribution.
Fermi-Dirac Distribution Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(p)=\frac{1}{\exp{(\frac{E(p)-\mu}{kT}})+1}}
Bose-Einstein Distribution Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(p)=\frac{1}{\exp{(\frac{E(p)-\mu}{kT}})-1}}
Maxwell-Boltzman Distribution Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(p)=\exp{(\frac{-(E(p)-\mu)}{kT})}}
In the above expressions "Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu} " represents the particles' chemical energy, "k" is the Boltzman constant and "T" is the temperature of the gas.
Also, in any of the expressions above, the particles contain energy Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E=\frac{p^{2}}{2m}} where the momentum Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p=mv} can be used interchangeably.
Basic Nuclear Physics
All nuclei are formed from combinations of protons and neutrons. These two particles are similar in mass:
Mass of Proton: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m_{p}} =938.272 Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle MeV/c^{2}}
Mass of Neutron: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m_{n}} =939.565 Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle MeV/c^{2}}
however, the proton has charge Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle +1e} while the neutron is electrically neutral.
These two types of particles interact with each other within the nucleus via two forces, the strong nuclear force and the Coulomb (electromagnetic) force. Since the Coulomb interaction is coupled to charged particles, it only affects protons; both protons and neutrons are sensitive to the strong nuclear force. However, the strong nuclear force is a very short-range force, active at separations of ~ 1 fm.
Binding Energy
The mass of a specific nuclei will be lower than the sum of its constituent particles, and the difference is called the binding energy of the nucleus:
Binding Energy: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B(Z,N)=Zm_{p}+Nm_{n}-M(Z,N)}
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m_{p}} is the proton mass, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m_{n}} is the neutron mass, and M(Z,N) is the mass of the nucleus, and Z and N play their usual roles as the proton and neutron number, respectively.
Main Nuclear Decays Between Driplines
When dealing with the behavior of an atom, one must consider first the stability of the atom (element). Some atomic arrangements are naturally stable, while others are unstable and quickly (or slowly) decay into other constituents. By changing the proton and neutron numbers of atoms you obtain different isotopes or elements. Only a certain number are stable and do not decay into other, smaller, atoms. Driplines are the conceptualized boundaries between stable and unstable atoms. When plotted, all the atoms together form the Table of Nuclides; showm below.
The Table of Nuclides is essentially the Nuclear Physics analogy of the Periodic Table of Elements. It summarizes all nuclear arrangements which are observed or calculated as stable, or unstable. The driplines are the lines bordering the upper and lower boundaries of the main sequence of stable atoms. Around these driplines, the unstable atoms will decay into other atoms, releasing energy. It is important to understand the characteristics of these types of decay in order to understand the nature of the atoms in question. There are four forces of our universe which govern virtually all of physical nature: Gravitational Force, Electromagnetic Force, Strong Nuclear Force and Weak Nuclear Force. The strong and weak forces are responsible for stong and weak decay interactions.
Strong Decays (Short time spans)
1. Alpha decay: Alpha Decay refers to when an atom decays via expelling a Helium nucleus from it's own nucleus. The following reaction takes place:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (Z,A)\rightarrow(Z-2,A-4)+^4He} where:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle M_{nuc}(^4He)+M_{nuc}(Z-2,A-4)\le M_{nuc}(Z,A)} and:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle M_{at}(^{4}He)+M_{at}(Z-2,A-4)\le M_{at}(Z,A)}
2. Fission: Fission refers to the process of the atom decaying (splitting) into essentially two equal pieces (approximately). Under this type of decay, the following reaction takes place:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (Z,A)\rightarrow(\approx\frac{Z}{2},\approx\frac{A}{2})} where:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2*M_{nuc}(\frac{Z}{2},\frac{A}{2})\le M_{nuc}(Z,A)} and:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2*M_{at}(\frac{Z}{2},\frac{A}{2})\le M_{at}(Z,A)}
Weak Interactions (Long time spans)
3. Beta Decay (Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta^-} ): This type of decay refers to the type of beta decay where an electon is expelled from the atom along with an accompanying electron antineutrino. This decay is given by the following reaction:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (Z,A)\rightarrow (Z+1,A)+e^{-}+\bar{\nu_e}} where:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle M_{nuc}(Z,A)\ge M_{nuc}(Z+1,A)+m_e} and:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle M_{at}(Z,A)\ge M_{at}(Z+1,A)}
4. Beta Decay (Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta^+} ): This type of decay refers to the type of beta decay in which a positron is expelled from the atom along with an electron neutrino as well. This type of decay is given by the following reaction.
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (Z,A)\rightarrow (Z-1,A)+e^{+}+\nu_e} where:
and:
5. Electron Capture: Electron capture is a different type of decay, in which the atom actually gains an electron and expells a neutrino instead, giving off energy. This is sometimes known as "inverse beta decay", however is often looked at as a type of beta decay regardless. This type of decay is reserved for atoms which are very proton rich and do not have enough energy to expell a positron and a neutrino (typically in environments with very high density and temperatures). The reaction is given by:
where:
and:
Role of the Coulomb Barrier in Nuclear Decays
When a nucleus decays, the decay particles must quantum tunnel through the potential barrier created by the nucleus' Coulomb potential. The probability of tunneling is, in the WKB approximation,
, where and are the radial positions of the Coulomb barrier at the particle's energy level, i.e. is the distance the particle must tunnel.
When the potential is the Coulomb potential, , the tunneling probability can be written as
, where . The value of is called the Sommerfeld parameter. Here, and are the electric charge of the parent nucleus and the decay particle, and E is the energy of the decay particle.
Nuclear Cross Sections
A critical part of understanding nunclear reactions is understanding the cross sections associated with different situations. There are different quantum mechanical potentials unique to certain conditions (such as the Coulomb Potential illustrated above) which change the Hamiltonian of a system, and thus allow differing wavefuctions for their respective regions. Based on the way these wavefunctions should behave, we can calculate the direct Transition Probabilities (i.e. the probability a wave or particle will "tunnel" through a potential barrier) for any general case, as follows:
Where the quantum mechanical flux "" can be defined as the flux of incoming particles (waves) in the reaction:
The "cross section" of a nuclear reaction is essentially a probability that a nuclear reaction will occur at all given the parameters of the nuclei and particles involved. It is effected by many contributing factors; notably the quantum mechanical potential being dealt with and the flux of incoming particles . It can be defined most generally as:
However, the cross section for a nuclear reaction can be expressed in terms of a summation over all possible angular momentum values and the respective transmission coefficients for those values as follows:
Where the summation above sums all contributing values for
It is important to properly describe the wave functions involved in these types of problems as well. Incoming plane waves represent incoming particles and can be defined as:
Again, summing over all contributing values. And the Bessel Functions can be approximated at large Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle kr} as:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle j_{l}(kr)\rightarrow \frac{\sin(kr-\frac{\pi l}{2})}{kr}}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sin(x)=\frac{\imath}{2}(e^{-\imath x}-e^{\imath x})}
Now, we can obtain definitions for our incoming and outgoing wavefunctions:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi_{in}=\frac{\sqrt{\pi}}{kr}\Sigma\sqrt{2l+1}\imath^{l+1}(e^{-\imath(kr-\frac{\pi l}{2})}-e^{\imath(kr-\frac{\pi l}{2})})Y_{l,0}}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi_{trans}=\frac{\sqrt{\pi}}{kr}\Sigma\sqrt{2l+1}\imath^{l+1}(e^{-\imath(kr-\frac{\pi l}{2})}-\eta_{l}e^{\imath(kr-\frac{\pi l}{2})})Y_{l,0}}
(Where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \eta} is described in section above, and summations are, again, over all contribultions of the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle l} components.)
After many derivations from this information we can redefine the cross section as follows (in more succinct form):
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma=\frac{-\int\vec{e}_{r}\vec{j}_{t} r^{2} d \Omega}{\vert\vec{j}_{in}\vert}}
Therefore, the total cross section for reactions can be described as:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma=\frac{\pi}{k^{2}}\Sigma(2l+1)(1-\vert\eta_{l}\vert^{2})=\frac{\pi}{k^{2}}\Sigma(2l+1)T_{l}}
This is exactly as was stated above. However, it should be noted that at low energies (of incoming projectiles), S-waves will dominate because the scattering probability "Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \eta_{l}} " decreases.
Thermonuclear Reactions
Understanding thermonuclear reactions is a vital piece of understanding a great number of astrophysical phenomena. The primary goal of understanding the behavior of different thermonuclear reactions essentially boils down to determining the energy and abundance changes of different nuclides involved in a given system. Thermonuclear reactions are most notably referred to (generally) as a nuclear fusion process occurring at very high temperatures in the interiors of stars. To begin with, before we can explore the deeper workings of thermonuclear reactions, we need to define the rate of nuclear reactions Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r} of a certain species "Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i} " with another species "Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle j} ":
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma=\frac{number\ of\ reactions\ target^{-1}sec^{-1}}{flux\ of\ incoming\ particles}=\frac{r/n_i}{n_jv}}
In order to experiment either (theoretically or actually) with thermonuclear reactions, therefore, all one needs to know are the cross sections "Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma} " and the velocity distribution of the beam and the target.
Assuming we are dealing with a non-degenerate Blotzman gas, we can define the reaction rates as:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r_{i,j}=n_in_j\int\sigma(\vert\vec{v}_i-\vec{v}_j\vert)\vert\vec{v}_i-\vec{v}_j\vert\phi(\vec{v}_i)\phi(\vec{v}_j)d^{3}v_{i}d^3v_{j}}
Or, more compactly: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r_{i,j}=n_{i}n_{j}\langle\sigma v\rangle_{i;j}}
Where: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi(\vec{v}_i)\phi(\vec{v}_j)=\frac{(m_{i}m_{j})^{3/2}}{(2\pi kT)^{3}}exp(-\frac{m_{i}v_{i}^{2}+m_{j}v_{j}^{2}}{2kT})}
Now, if we transform this relationship into a center of mass frame using Newton's Laws, we can obtain an expression for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle\sigma v\rangle} and if we know the abundances of each species we can easily calculate their reaction rates:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle\sigma v\rangle(T)= (\frac{8}{\mu\pi})^{1/2}\frac{1}{(kT)^{3/2}}\int E\sigma(E)exp(-\frac{E}{kT})dE}
Where "Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E} " is integrated from infinity to zero (over all positive values).
Now, from the above equation if we know the energy of a system of particles and can correctly solve it, then we can derive reaction rates for specific types of reactions such as Resonant Reactions (typical at relatively low temperatures), Non-Resonant Reactions for Neutrons (s-waves with l=0) and Non-Resonant Reactions for charged particles.
The "Big Bang" and Early Universe
Understanding our universe as it is today requires an understanding of what happened before today. In order to do this, we are required to maintain certain assumptions about the universe we live in. To begin with, it is a rather obvious assumption that the universe is extremely large. In addition to being unfathomably huge, and old, we assume that in general the universe is made of the same material as Earth. This can be summed up in the Cosmological Principle: "When averaged over a large enough volume, the universe appears the same in all locations." This speaks to the homogeneity of our universe and is a cornerstone in subsequent calculations. However this principle bears with it many other implications as well; such as the fact that the universe must not have boundaries and that any volume this principle is applied to must be greater than 500Mpc.
The Friedman Equation is an equation which governs the expansion of an isotropic gas, and is able to be used because we assume the universe is more or less homogeneous on large enough scales.
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (\frac{\dot{R}}{R})^{2}=H^{2}(t)=\frac{8 \pi G \rho}{3}-\frac{kc^{2}}{R^{2}}}
Above, "" represents the scale parameter and "" determines the geometry of the universe. Where here, we have three cases:
Main Sequence Stars
The Main Sequence contains stars in a distinctive band on the Hertzsprung-Russell diagram, correlating luminosity to temperature. A majority of stars are along the main sequence, which is predictable due to the fact that Main Sequence stars are fusing hydrogen, something stars will spend most of their time doing.
Hydrostatic Equilibrium and Equations of Stellar Structure
Hydrostatic Equilibrium in stellar structures is a very important idea because it allows us to approximate/calculate various equations of states of differing types of stars based on the idea that things "are not changing very much". More precisely, a "fluid element" (volume element of gas inside a star) is balanced and essentially held in place by the balancing forces of the inward pull of gravity with the outward force of the gas's pressure gradient.
Force of Pressure Gradient:
Force of Gravity:
For these two forces to balance we require that:
From these equations we can gather simple estimates for stellar structures and their equations of states:
Pressure Equilibrium:
Conservation of Mass:
It is important to note (however obvious) that the mass of a star (and therefore it's density as well) is not uniformly distributed. The vast majority of the mass is concentrated at a star's center and therefore the star's core is incredibly dense; while the outer regions of a star's interior have very little mass and are therefore not very dense at all.
However, the star looses energy everywhere at it's surface in the form of heat, and more importantly, light. We measure this loss of energy in a star as Luminosity. In fact, in order to keep the temperature constant everywhere, luminosity must be generated. This generation of energy is comprised of all nuclear processes within the star that generate the star's energy. This rate of energy generation is known as "". We approximate the star(s) as a spherical surface, radiating energy at a radius "". Therefore, the energy equation can be described as (where "" is the star's Luminosity):
Energy Generation Equation:
A star's luminosity is generated at it's center, and increases as various nuclear processes carry the energy to the surface of the star at which point the star's luminosity is a constant value. Therefore, the temperature inside a star must increase as you approach the center in order to allow for energy transportation from the star's center to it's surface. This energy transport (or convection) can be described by the Energy Transport Equation:
Energy Transport Equation:
Chain of Reactions/Reaction Rates
Inside stars (primarily main-sequence stars), the energy necessary to sustain the star derives from various chains of nuclear reactions. In general, these stars begin with consisting primarily of a species (usually Hydrogen) and burn it at a specific rate into another species . The species is thus burned to create species and so on. When we look at this relationship, we see that the series (chain) of reactions depicts a specific pattern, which deems every species "i" that decays into a species "i+1" depend on the previous state "i". Likewise, the state "i+1" decays into "i+2" and so species "i+1" will also depend on species "i+2" as well. Therefore, if we begin with a species "1", which decays into species "2", and then decays into species "3", the abundance of species "2" can be defined as:
where:
However, under these circumstances, we must make a couple assumptions regarding these reactions. First of all we assume that in the above example is a constant (essentially, because depletion is very slow due to the bottle neck) and that the capture rates are constant as well.
However, under these assumtions where , then after some time will reach an equilibrium abundance. Once at equilibrium:
and
This relationship continues for the remainder of the chain up to "" species where the abundances times the rates are all equal. This is called "Steady State".
Neutrino Physics
Neutrinos are very lightweight (~eV), electrically neutral leptons which are necessary for weak reactions to commence. The lepton number of a system must be conserved, so whenever a beta-plus or beta-minus reaction occurs ( or ), a neutrino is required to keep the lepton number constant as well as to conserve linear and angular momentum.
Historically, there were three massless neutrinos, one corresponding to each lepton: the electron neutrino (), the muon neutrino (), and the tau neutrino (). This understanding produced problems when neutrinos developed by the sun's fusion were measured: only about a third of the expected neutrinos were actually detected by the Homestead Experiment, a late-1960's experiment conducted by Raymond Davis, Jr and John Bahcall.
For the next thirty years, the neutrino deficit was a major unsolved problem in physics. It was only resolved in the early 2000's when it was found by the Sudbury Neutrino Observatory (which was capable of detecting tau and muon neutrinos as well as the expected electron neutrinos) that the neutrinos oscillated in their flavor as they propagated from the core of the sun to the Earth. Current theories of stellar structure and nuclear physics predicted that electron neutrinos from the PP chain reactions occurring in the sun's core would propagate to the Earth, when in fact these electron neutrinos were oscillating in their flavor, becoming tau and muon neutrinos.
Stellar Burning Cycles
Stars undergo a variety of different evolutions based on their original chemical composition, mass, density and other traits. Most stars in early burning stages are primarily composed of Hydrogen (the most abundant element in the universe). Through the series of PP (proton-proton) reactions, Hydrogen is fused together to form Helium. Helium is then (once it becomes abundant enough) fused together to make Carbon, Nitrogen, and Oxygen (CNO Cycle). This is the process by which Helium is consumed. However, stars can undergo a variety of different changes based on their mass.
: Matter is not processed
: Star undergoes partial Hydrogen burning
: Complete Hydrogen burning, but no Helium burning
: There is incomplete Helium burning; and Carbon-12 is enhanced, while there is no Oxygen-16 produced
: There is complete Hydrogen burning, then the star moves on to more advanced burning stages
The mass of a star is directly correlated to the burning conditions observed, and the elements the star's burning produces.
Origin of Heavy Elements
When discussing the origin of "Heavy Elements", we typically refer to atomic masses heavier than FeI (Iron I). First of all, if we were to plot the universe's abundances of all elements/nuclides as a function of atomic mass number, we would notice that nuclides with mass numbers greater than Fe are far less abundant. These "heavy" atoms are formed from a series of neutron captures and subsequent decays. The process can be broken into two distinct forms of the process: the r-process and the s-process.
S-Process: Referrs to "slow" neutron capture with respect to decays and weak interactions. The s-process is responsible for approximately half the stable, heavy elements beyond the iron peak and occurrs in stars with low neutron density and [relatively] low temperatures. Heavier elements are formed via the process of capturing a neutron and becoming an unstable isotope of the original element. Under the neutron conditions described above the average time for another neutron capture to occurr is far greater than the average time of a decay to occurr so the nucleus almost immediately decays to a heavier, stable element. Therefore the s-process propagates strictly in the valley of stable isotopes and "zig-zags" its way to the top of the table of nuclides diagonally.
R-Process Referrs to "rapid" neutron capture with respect to deays and weak interaction. It is responsible for roughly the other half of all nuetron-rich atoms in the universe and is most common during core collapse of supernovae. Here, the neutron density is much higher and so neutron capture on stable elements occurrs much more rapidly. Stable "seed" elements are bombarded with rapid neutron captures and extend far into the neutron dripline territory on the table of nuclides. These highly unstable isotopes then subsequently decay to form stable nuclei.
It is important to note here that both these processes include neutron capture and subsequent decays, however the rate of neutron capture dictates how the heavier elements are built up. This capture rate is determined by the temperature of the region, and the neutron density. This process would extrapolate forever, except for the fact that once the elements' atomic mass number reaches 200, they begin to become very decay unstable and begin decaying faster than they are created.
Under these processes, the rate equations governing atomic abundances reduces to:
where:
So, we're left with:
When solving the above rate equation for the abundances of subsequent nuclei, it is important to state that it abides by "Stationarity". That is, given the conditions of the processes, we can essentially state each component is constant.
It is also important to note that niether of these processes would be possible without "seed" nuclei. Seed nuclei are usually the elements Fe (s-process) or Ni (r-process) and serve as the somewhat heavy elements that must be present to begin capturing neutrons in the first place (in abundances of at least 0.04).