Solution to Set 5: Difference between revisions

From PhyWiki
Jump to navigation Jump to search
 
(78 intermediate revisions by 5 users not shown)
Line 1: Line 1:
<font color="blue"> I have no idea what I'm doing - [[User:KimberlyWynne|KimberlyWynne]] 03:11, 2 March 2009 (EST)</font>
'''Diatomic harmonic chain'''
'''Diatomic harmonic chain'''


==Problem 1==
==Problem 1==
'''Given:'''
I found this site somewhat helpful and explanatory:
 
http://newton.ex.ac.uk/teaching/resources/rjh/phy2009/PHY2009handout13.pdf
 
===Given===
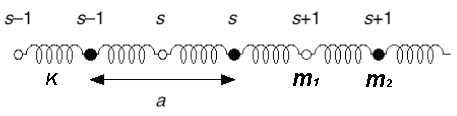
* a chain of atoms  
* a chain of atoms  
* with alternating masses <math>m_1\;</math> and <math>m_2\;</math>
* with alternating masses <math>m_A\;</math> and <math>m_B\;</math>
* connected with elastic springs with constant <math>K\;</math>
* connected with elastic springs with constant <math>Q\;</math>
* moving only in the x-direction
* moving only in the x-direction


Line 14: Line 16:
'''Derive the dispersion relation <math>\omega^{\alpha} (k)\;</math> for this chain'''
'''Derive the dispersion relation <math>\omega^{\alpha} (k)\;</math> for this chain'''


=== Index <math>\alpha = 1\;</math> for acoustic branch ===
When solving problem 1 one can arrive at the same solution in two different ways. Both methods will be solved for completeness of this solution.
===Model 1===


Potential Energy <math>U = 1, 2, 3, ... n \;</math>
Model 1 involves having two separate displacement vectors so that the equations of motion may be solved independently. Let u be the displacement vector for type A atoms and v be the displacement vector for the B atoms.
The equations of motion for any of these particles is given by:


<math>U \cong \frac{1}{2} k \sum_{n} (U_n - U_{n-1}) \;</math>
<math>m_A \ddot{u}_n = - Q [2u_n - v_{n} - v_{n-1}] \;</math>


<math>\Rightarrow m \ddot{U}_n = - k [2U_n - U_{n-1} - U_{n+1}] = -m \omega U(t) \;</math>
<math>m_B \ddot{v}_n = - Q [2v_n - u_{n} - u_{n+1}] \;</math>


Eigenvectors of Modes A and B (defined arbitrarily)
Then since this is a chain of harmonic oscillators one can assume a solution for u and v for a given n.


<math>u_m(t)=e^{i\omega t} u_m \;</math>
<math>u_n = C e^{i(kna-\omega t)}\;</math>


<math>\Rightarrow -m \omega ^2 \ddot{\vec{u}}_n = - k \mathbf{M} \vec{u} \;</math>
<math>v_n = D e^{i(kna-\omega t)}\;</math>


Band Matrix
These equations add the wavenumber k, the periodicity length a, and the frequency <math>\omega</math>. Then substituting these solutions into the equations of motion one gets:
 
<math>-\omega^2 m_A C e^{i(kna-\omega t)} = Q (De^{i(kna-\omega t)} + De^{i(k(n-1)a-\omega t)} - 2 C e^{i(kna-\omega t)}) \;</math>
 
<math>-\omega^2 m_B D e^{i(kna-\omega t)} = Q (Ce^{i(kna-\omega t)} + Ce^{i(k(n+1)a-\omega t)} - 2 D e^{i(kna-\omega t)}) \;</math>
 
Then dividing both equations by <math> e^{i(kna-\omega t)}</math> one gets:
 
<math>-\omega^2 m_A C = Q (D + De^{-ika} - 2  C) \;</math>
 
<math>-\omega^2 m_B D = Q (Ce^{ika} + C - 2 D) \;</math>
 
Rearranging these equations one gets:


<math>
<math>
\mathbf{M} = \begin{vmatrix}
\begin{vmatrix}
2 & 1 & 0 & 0\\  
2Q-m_A\omega^2 & -Q-Qe^{-ika}\\  
1 & 2 & 1 & 0\\  
-Q-Qe^{ika} & 2Q-m_B\omega^2
0 & 1 & 2 & 1\\  
\end{vmatrix}
0 & 0 & 1 & 2
\begin{vmatrix}
C \\ D
\end{vmatrix}
\end{vmatrix}
=0
</math>
</math>


Running waves through a solid
Since we are concerned with the non-trivial solutions of these equations the determinant must be zero. Therefore one gets
<math>(2Q-m_A\omega^2)(2Q-m_B\omega^2) - Q^2\left(1+e^{-ika}\right)(1+e^{ika}) = 0 </math>
 
<math>m_Am_B\omega^4 - 2Q\left(m_A + m_B\right)\omega^2 + 4Q^2 - 2Q^2 - Q^2e^{-ika} - Q^2e^{ika}</math>


<math>u_m (t) = e^{ik(na)- \omega t} = e^{i k R_n} \;</math>  
<math>m_Am_B\omega^4 - 2Q(m_A + m_B)\omega^2 + 4Q^2 - 4Q^2cos^2\left({ka \over 2}\right)</math>


where
<math>m_Am_B\omega^4 - 2Q(m_A + m_B)\omega^2 + 4Q^2sin^2\left({ka \over 2}\right)</math>


<math>u_m \rightarrow  u_n e^{ik(na)} \;</math>
Then one needs to solve this quadratic equation for omega squared.


<math>R_n \;</math> = distance on some coordinate system
<math>\omega^2 = \frac{2Q(m_A+m_B)\pm\sqrt{4Q^2(m_A+m_B)^2-4m_Am_B(4Q^2sin^2(ka/2))} }{2m_Am_B} \;</math>


<math>\Rightarrow -m \omega ^2 \vec{u} = - k [2 - e^{ik \alpha} - e^{-ik \alpha}] \;</math>
<math>\omega^2 = Q({1 \over m_B} + {1 \over m_A}) \pm Q\sqrt{( {1 \over m_B}+ {1 \over m_A})^2 - {4 \over m_A m_B} sin^2({ka \over 2})}</math>


Derive and get:
From here one can find the two branches of the frequency.


<math>\Rightarrow \omega (k) = 2 \sqrt{ \frac{k}{m} } |sin(ka)|</math>
Acoustical:
<math>\omega_A^2 = Q({1 \over m_B} + {1 \over m_A}) + Q\sqrt{( {1 \over m_B}+ {1 \over m_A})^2 - {4 \over m_A m_B} sin^2({ka \over 2})}</math>


=== '''Index<math>\alpha = 2\;</math> for optical branch''' ===
With individual frequencies
<math>\omega_A = \pm \sqrt{Q({1 \over m_B} + {1 \over m_A}) + Q\sqrt{( {1 \over m_B}+ {1 \over m_A})^2 - {4 \over m_A m_B} sin^2({ka \over 2})}}</math>


<math>u_m (t) = e^{ik(na)- \omega t} = e^{i k R_n} \;</math>  
And Optical:
<math>\omega_O^2 = Q({1 \over m_B} + {1 \over m_A}) - Q\sqrt{( {1 \over m_B}+ {1 \over m_A})^2 - {4 \over m_A m_B} sin^2({ka \over 2})}</math>


<math>u(R_n) \equiv e^{i k R_n} = cos (k a) \;</math>
With individual frequencies
<math>\omega_O = \pm \sqrt{Q({1 \over m_B} + {1 \over m_A}) - Q\sqrt{( {1 \over m_B}+ {1 \over m_A})^2 - {4 \over m_A m_B} sin^2({ka \over 2})}}</math>


<math>\Rightarrow - m \omega^2 e^{ikna} = -k [2e^{ik(na)} - e^{ik(n+1)a} - e^{ik(n-1)a}] \;</math>
===Model 2===


<math>\Rightarrow m \omega^2 = k [2 - (e^{ika}  + e^{-ika})] \;</math>
Model 2 involves having one displacement vector, U. Though there is only one displacement vector, there still will be two equations of motion, one for the even numbered atoms (type A) and one for the odd numbered atoms (type B).
The equations of motion for any of these particles is given by:


<math>\Rightarrow \omega^2 = \frac{2k}{m} [1 - cos(ka)] \;</math>
<math>m_A \ddot{U}_{2n} = - Q [2U_{2n} - U_{2n-1} - U_{2n+1}] </math>


<math>\Rightarrow \omega^2 = \frac{\Delta k}{m} \frac{1}{2} [1 - cos(ka)] \;</math>
<math>m_B \ddot{U}_{2n+1} = - Q [2U_{2n+1} - U_{2n} - U_{2n+2}] </math>


<math>\Rightarrow \omega^2 = \frac{\Delta k}{m} sin^{2}(\frac{ka}{2}) \;</math>
Note that the subscript 2n (rather than just n) is used to guarantee that the value is even.
Again since this is a chain of harmonic oscillators one can assume a solution for the even and odd entries of U.


<math>\Rightarrow \omega (k) = 2 \sqrt{ \frac{k}{m} } |sin(\frac{ka}{2})| \;</math>
<math>U_{2n} = C e^{i(2kna-\omega t)}\;</math>


[[Image:Dispersionrelation.jpg]]
<math>U_{2n+1} = D e^{i(k(2n+1)a-\omega t)}\;</math>
 
Then substituting these solutions into the equations of motion one gets:
 
<math>-\omega^2 m_A C e^{i(ka(2n)-\omega t)} = Q (De^{i(ka(2n+1)-\omega t)} + De^{i(k(2n-1)a-\omega t)} - 2 C e^{i(k(2n)a-\omega t)}) \;</math>
 
<math>-\omega^2 m_B D e^{i(ka(2n+1)-\omega t)} = Q (Ce^{i(k(2n)a-\omega t)} + Ce^{i(k(2n+2)a-\omega t)} - 2 D e^{i(k(2n+1)a-\omega t)}) \;</math>
 
Then dividing the top equation by <math>e^{i(ka(2n)-\omega t)}</math> and the bottom equation by <math> e^{i(ka(2n+1)-\omega t)}</math> one gets:
 
<math>-\omega^2 m_A C = Q (De^{ika} + De^{-ika} - 2 Q C) \;</math>
 
<math>-\omega^2 m_B D = Q (Ce^{ika} + Ce^{-ika} - 2 D) \;</math>
 
And after rearranging to a matrix system one gets:
 
<math>
\begin{vmatrix}
2Q-m_A\omega^2 & Q(e^{-ika}+e^{ika})\\
Q(e^{ika}+e^{-ika}) & 2Q-m_B\omega^2
\end{vmatrix}
\begin{vmatrix}
C \\ D
\end{vmatrix}
=0
</math>
 
Again we are concerned with the non-trivial solutions of these equations the determinant must be zero. And one gets
<math>(2Q-m_A\omega^2)(2Q-m_B\omega^2) - Q^2\left(e^{ika}+e^{-ika}\right)(e^{-ika}+e^{ika}) = 0 </math>
 
<math>m_Am_B\omega^4 - 2Q\left(m_A + m_B\right)\omega^2 + 4Q^2 - 2Q^2 - Q^2e^{-2ika} - Q^2e^{2ika}</math>
 
<math>m_Am_B\omega^4 - 2Q\left(m_A + m_B\right)\omega^2 + 4Q^2 - 2Q^2 - Q^2e^{-2ika} - Q^2e^{2ika}</math>
 
<math>m_Am_B\omega^4 - 2Q(m_A + m_B)\omega^2 + 4Q^2 - 4Q^2cos^2\left(ka\right)</math>
 
<math>m_Am_B\omega^4 - 2Q(m_A + m_B)\omega^2 + 4Q^2sin^2\left(ka\right)</math>
 
Note the difference of the argument of the sin function. This is the major change in the derivation of these two methods.
 
Then solving for omega squared:
 
<math>\omega^2 = \frac{2Q(m_A+m_B)\pm\sqrt{4Q^2(m_A+m_B)^2-4m_Am_B(4Q^2sin^2(ka))} }{2m_Am_B} \;</math>
 
<math>\omega^2 = Q({1 \over m_B} + {1 \over m_A}) \pm Q\sqrt{( {1 \over m_B}+ {1 \over m_A})^2 - {4 \over m_A m_B} sin^2(ka)}</math>
 
From here one can find the two branches of the frequency.
 
Acoustical:
<math>\omega_A^2 = Q({1 \over m_B} + {1 \over m_A}) + Q\sqrt{( {1 \over m_B}+ {1 \over m_A})^2 - {4 \over m_A m_B} sin^2(ka)}</math>
 
With individual frequencies
<math>\omega_A = \pm \sqrt{Q({1 \over m_B} + {1 \over m_A}) + Q\sqrt{( {1 \over m_B}+ {1 \over m_A})^2 - {4 \over m_A m_B} sin^2(ka)}}</math>
 
And Optical:
<math>\omega_O^2 = Q({1 \over m_B} + {1 \over m_A}) - Q\sqrt{( {1 \over m_B}+ {1 \over m_A})^2 - {4 \over m_A m_B} sin^2(ka)}</math>
 
With individual frequencies
<math>\omega_O = \pm \sqrt{Q({1 \over m_B} + {1 \over m_A}) - Q\sqrt{( {1 \over m_B}+ {1 \over m_A})^2 - {4 \over m_A m_B} sin^2(ka)}}</math>


==Problem 2==
==Problem 2==
Determine the speed of sound for this chain. What is the lowest frequency of long-wavelength sound corresponding to the optical branch?
Determine the speed of sound for this chain.  


<math>\omega _{\alpha }(k)\approx C_{\alpha } k \;</math>
<math>\omega _{\alpha }(k)\approx C_{\alpha } k \;</math>
Line 84: Line 169:
* <math>\omega_{\alpha } \;</math> = frequency
* <math>\omega_{\alpha } \;</math> = frequency
* <math> C_{\alpha } \;</math> = speed of sound
* <math> C_{\alpha } \;</math> = speed of sound
* <math> k \;</math> = ???
 
Therefore the speed of sound:
 
<math>C_{\alpha} = \frac{\omega}{k} = a \sqrt{\frac{k}{2(m_1+m_2)}} \;</math>
 
What is the lowest frequency of long-wavelength sound corresponding to the optical branch?
 
<math>\omega_{low} = \sqrt{\frac{2k}{m}}</math>


==Problem 3==
==Problem 3==
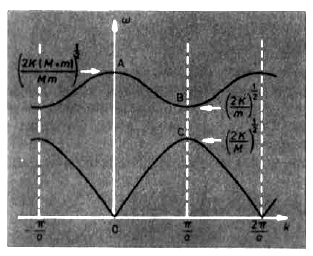
Sketch the motion of the atoms corresponding to the edge of the Brillouin zone, both for the optical and the acoustic branch.
Sketch the motion of the atoms corresponding to the edge of the Brillouin zone, both for the optical and the acoustic branch.
[[Image:Dispersionbranches.jpg]]
* Acoustic Branch: lower branch
* Optical Branch: upper branch, as <math>k \rightarrow 0 </math> on this branch the vibrations of the 2 types of atom are in antiphase and the resulting charge oscillation in an ionic craystal give a strong coupling to electromagnetic waves at the frequency of point A.


==Problem 4==
==Problem 4==
Determine the Debye temperature for this system, and determine the form of the specific heat <math>c_V (T)</math> in the limits of high and low temperatures.  
Determine the Debye temperature for this system, and determine the form of the specific heat <math>C_V (T)</math> in the limits of high and low temperatures.
 
===Debye Temperature <math>T_D \;</math>===
The Debye temperature, aka the effective sonic velocity, is a measure of the hardness of the crystal
 
From our class lectures:
 
<math>k_B T_D = \hbar \omega_D = \hbar c k_D \;</math>
 
or <math> T_D = \dfrac {\hbar \omega_D}{k_B}</math>
 
The Debye Frequency is defined as
 
<math>\omega_D = (\dfrac {3 N}{4 \pi V})^\frac {1}{3} \omega_s</math>
 
where <math>\omega_s</math> is the speed of sound defined above.
 
Considering the fact that this is a one-dimensional system, the Debye Frequency is going to be slightly different.
 
<math>\omega_D = \dfrac {N}{L} \omega_s</math>  is the frequency for the one-dimensional case.
 
===Specific Heat <math>C_V \;</math>===
Specific Heat in a solid is defined as
 
<math>C_v = \frac {\partial U}{\partial T}</math>
 
where U is the total energy of the system, and T is the temperature of the system.
 
We know that the energy of a phonon system is
 
<math> E = h \nu = \dfrac {h v_s n}{2 L}  </math>
 
And the total energy according to the Bose-Einstein Distribution is
 
<math>U = \int \limits _{0} ^{E_{max}} \dfrac {E} {e^{\frac {E}{k_b T}}-1} \, dE </math>
 
For the one-dimensional case, making the integral depend on n.
 
<math>U = \int \limits _{0} ^{n_{max}} \dfrac {h v_s n}{2 L} \dfrac {1}{e^{\frac {h v_s n} {2 L k_B T}}-1}\,dn</math>
 
Substituting in the equation
 
<math>x = \dfrac {h v_s n} {2 L k_B T}</math>
 
and <math>x_{max}=\dfrac {h v_s n_{max}} {2 L k_B T} = \dfrac {h v_s} {2 k_B T} \dfrac {N}{L} = \frac {T_D}{T}</math>
 
We are left with the following Equation:
 
<math>U=\dfrac {N k_b T^2}{T_D} \int \limits _0 ^{\frac {T_D}{T}} \dfrac {x}{e^x - 1} \, dx</math>
 
Now this is hard to solve overall for, but an approximation can be found for low temperatures and high temperatures.
 
 
==== Low Temperature Limit ====
We have the integral:
 
<math>U=\dfrac {N k_b T^2}{T_D} \int \limits _0 ^{\frac {T_D}{T}} \dfrac {x}{e^x - 1} \, dx</math>
 
And on low temperatures, much smaller than the Debye temperature it is as if the upper limit is infinite.  We can use the substitution for the integral:
 
<math>\int \limits _0 ^\infin \dfrac {x} {e^x-1}\, dx =\dfrac {\pi ^2}{6} </math>
 
Substituting that into the equation for the Energy, we are left with
 
<math>U=\dfrac {N k_b \pi^2}{6 T_D} \, T^2 </math>
 
and our Specific heat is now
 
<math>C_V=\dfrac {dU}{dT} =\dfrac {N k_b \pi^2}{3 T_D} \, T</math>
 
 
==== High Temperature Limit ====
We have the integral:
 
<math>U=\dfrac {N k_b T^2}{T_D} \int \limits _0 ^{\frac {T_D}{T}} \dfrac {x}{e^x - 1} \, dx</math>
 
which can not be solved analytically.  However, at high temperatures above the Debye Temperature, the value of x is very small and we can use the approximation that <math>e^x=1+x</math>.
 
Which leaves us with the (much easier to solve) integral of
 
<math>U=\dfrac { N k_b T^2}{T_D} \int \limits _0 ^{\frac {T_D}{T}} \, dx</math>
 
Which reduces to
 
<math>U= N k_b T \,</math>
 
Then the specific heat is equal to
 
<math>C_V=\dfrac {dU}{dT} = N k_b \,</math>


==Problem 5==
==Problem 5==
Consider low temperatures (<math> T \ll T_D\;</math>) and determine the wavelength of the most abundant phonons <math>\lambda_{max}</math> (Hint: note the analogy with Wien's Law!)
Consider low temperatures (<math> T \ll T_D\;</math>) and determine the wavelength of the most abundant phonons <math>\lambda_{max}</math>  
 
===Given===
 
* Bose-Einstein Distribution <math>f(E)=\frac{1}{e^{E / k_B T}-1} \;</math>
** <math>f(E) \;</math> = probability that a particle will have energy E
** <math>k_B \;</math> = Boltzmann constant
** <math>T \;</math> = Temperature
 
* Planck's Radiation Formula <math>E = \frac{h \omega}{e^{h \omega / k_B T} - 1} \;</math>
** Density by frequency: <math>\rho (\omega) = \frac{dn_s}{d\omega} = \frac{8 \pi}{c^3} \omega^{2} \;</math>
** Density by wavelength: <math>\rho (\lambda) = \frac{dn_s}{d\lambda} = \frac{8 \pi}{\lambda^{4}} \;</math>
 
* Wien's law <math>\lambda_{\mathrm{max}} = \frac{b}{T} \;</math>
** <math>\lambda_max \;</math> is the peak wavelength in meters,
** <math>T \;</math> = temperature of the blackbody in Kelvin
** <math>b \;</math> = Wien's displacement constant
 
===Planck's Radiation Formula===
 
<math>S_\lambda = \frac{8 \pi h c}{\lambda^3} \frac{1}{e^{\frac{hc}{\lambda k t}}-1} \;</math>
 
Take the derivative and set = 0 to find the maximum
 
<math>\frac {\partial S_\lambda}{\partial \lambda} = - \frac{(3kt\lambda-ch)e^{\frac{ch}{kt\lambda}}-3kt\lambda} {kt\lambda^5e^{\frac{2ch}{kt\lambda}}-2kt\lambda^5e^{\frac{2ch}{kt\lambda}}+kt\lambda^5} \;</math>
 
<math>0 = - \frac{(3kt\lambda-ch)e^{\frac{ch}{kt\lambda}}-3kt\lambda} {kt\lambda^5e^{\frac{2ch}{kt\lambda}}-2kt\lambda^5e^{\frac{2ch}{kt\lambda}}+kt\lambda^5} \;</math>
 
<math>0 = - (3kt\lambda-ch)e^{\frac{ch}{kt\lambda}}-3kt\lambda \;</math>
 
<math>\lambda_{max} T = 2.898 \times 10^{-3} m\cdot K \;</math>

Latest revision as of 21:50, 31 March 2009

Diatomic harmonic chain

Problem 1

I found this site somewhat helpful and explanatory:

http://newton.ex.ac.uk/teaching/resources/rjh/phy2009/PHY2009handout13.pdf

Given

  • a chain of atoms
  • with alternating masses Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m_A\;} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m_B\;}
  • connected with elastic springs with constant Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Q\;}
  • moving only in the x-direction

Chainatoms.jpg

Derive the dispersion relation Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega^{\alpha} (k)\;} for this chain

When solving problem 1 one can arrive at the same solution in two different ways. Both methods will be solved for completeness of this solution.

Model 1

Model 1 involves having two separate displacement vectors so that the equations of motion may be solved independently. Let u be the displacement vector for type A atoms and v be the displacement vector for the B atoms. The equations of motion for any of these particles is given by:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m_A \ddot{u}_n = - Q [2u_n - v_{n} - v_{n-1}] \;}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m_B \ddot{v}_n = - Q [2v_n - u_{n} - u_{n+1}] \;}

Then since this is a chain of harmonic oscillators one can assume a solution for u and v for a given n.

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u_n = C e^{i(kna-\omega t)}\;}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle v_n = D e^{i(kna-\omega t)}\;}

These equations add the wavenumber k, the periodicity length a, and the frequency Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega} . Then substituting these solutions into the equations of motion one gets:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -\omega^2 m_A C e^{i(kna-\omega t)} = Q (De^{i(kna-\omega t)} + De^{i(k(n-1)a-\omega t)} - 2 C e^{i(kna-\omega t)}) \;}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -\omega^2 m_B D e^{i(kna-\omega t)} = Q (Ce^{i(kna-\omega t)} + Ce^{i(k(n+1)a-\omega t)} - 2 D e^{i(kna-\omega t)}) \;}

Then dividing both equations by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e^{i(kna-\omega t)}} one gets:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -\omega^2 m_A C = Q (D + De^{-ika} - 2 C) \;}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -\omega^2 m_B D = Q (Ce^{ika} + C - 2 D) \;}

Rearranging these equations one gets:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{vmatrix} 2Q-m_A\omega^2 & -Q-Qe^{-ika}\\ -Q-Qe^{ika} & 2Q-m_B\omega^2 \end{vmatrix} \begin{vmatrix} C \\ D \end{vmatrix} =0 }

Since we are concerned with the non-trivial solutions of these equations the determinant must be zero. Therefore one gets Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (2Q-m_A\omega^2)(2Q-m_B\omega^2) - Q^2\left(1+e^{-ika}\right)(1+e^{ika}) = 0 }

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m_Am_B\omega^4 - 2Q\left(m_A + m_B\right)\omega^2 + 4Q^2 - 2Q^2 - Q^2e^{-ika} - Q^2e^{ika}}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m_Am_B\omega^4 - 2Q(m_A + m_B)\omega^2 + 4Q^2 - 4Q^2cos^2\left({ka \over 2}\right)}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m_Am_B\omega^4 - 2Q(m_A + m_B)\omega^2 + 4Q^2sin^2\left({ka \over 2}\right)}

Then one needs to solve this quadratic equation for omega squared.

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega^2 = \frac{2Q(m_A+m_B)\pm\sqrt{4Q^2(m_A+m_B)^2-4m_Am_B(4Q^2sin^2(ka/2))} }{2m_Am_B} \;}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega^2 = Q({1 \over m_B} + {1 \over m_A}) \pm Q\sqrt{( {1 \over m_B}+ {1 \over m_A})^2 - {4 \over m_A m_B} sin^2({ka \over 2})}}

From here one can find the two branches of the frequency.

Acoustical: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega_A^2 = Q({1 \over m_B} + {1 \over m_A}) + Q\sqrt{( {1 \over m_B}+ {1 \over m_A})^2 - {4 \over m_A m_B} sin^2({ka \over 2})}}

With individual frequencies Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega_A = \pm \sqrt{Q({1 \over m_B} + {1 \over m_A}) + Q\sqrt{( {1 \over m_B}+ {1 \over m_A})^2 - {4 \over m_A m_B} sin^2({ka \over 2})}}}

And Optical: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega_O^2 = Q({1 \over m_B} + {1 \over m_A}) - Q\sqrt{( {1 \over m_B}+ {1 \over m_A})^2 - {4 \over m_A m_B} sin^2({ka \over 2})}}

With individual frequencies Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega_O = \pm \sqrt{Q({1 \over m_B} + {1 \over m_A}) - Q\sqrt{( {1 \over m_B}+ {1 \over m_A})^2 - {4 \over m_A m_B} sin^2({ka \over 2})}}}

Model 2

Model 2 involves having one displacement vector, U. Though there is only one displacement vector, there still will be two equations of motion, one for the even numbered atoms (type A) and one for the odd numbered atoms (type B). The equations of motion for any of these particles is given by:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m_A \ddot{U}_{2n} = - Q [2U_{2n} - U_{2n-1} - U_{2n+1}] }

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m_B \ddot{U}_{2n+1} = - Q [2U_{2n+1} - U_{2n} - U_{2n+2}] }

Note that the subscript 2n (rather than just n) is used to guarantee that the value is even. Again since this is a chain of harmonic oscillators one can assume a solution for the even and odd entries of U.

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U_{2n} = C e^{i(2kna-\omega t)}\;}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U_{2n+1} = D e^{i(k(2n+1)a-\omega t)}\;}

Then substituting these solutions into the equations of motion one gets:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -\omega^2 m_A C e^{i(ka(2n)-\omega t)} = Q (De^{i(ka(2n+1)-\omega t)} + De^{i(k(2n-1)a-\omega t)} - 2 C e^{i(k(2n)a-\omega t)}) \;}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -\omega^2 m_B D e^{i(ka(2n+1)-\omega t)} = Q (Ce^{i(k(2n)a-\omega t)} + Ce^{i(k(2n+2)a-\omega t)} - 2 D e^{i(k(2n+1)a-\omega t)}) \;}

Then dividing the top equation by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e^{i(ka(2n)-\omega t)}} and the bottom equation by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e^{i(ka(2n+1)-\omega t)}} one gets:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -\omega^2 m_A C = Q (De^{ika} + De^{-ika} - 2 Q C) \;}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -\omega^2 m_B D = Q (Ce^{ika} + Ce^{-ika} - 2 D) \;}

And after rearranging to a matrix system one gets:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{vmatrix} 2Q-m_A\omega^2 & Q(e^{-ika}+e^{ika})\\ Q(e^{ika}+e^{-ika}) & 2Q-m_B\omega^2 \end{vmatrix} \begin{vmatrix} C \\ D \end{vmatrix} =0 }

Again we are concerned with the non-trivial solutions of these equations the determinant must be zero. And one gets Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (2Q-m_A\omega^2)(2Q-m_B\omega^2) - Q^2\left(e^{ika}+e^{-ika}\right)(e^{-ika}+e^{ika}) = 0 }

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m_Am_B\omega^4 - 2Q\left(m_A + m_B\right)\omega^2 + 4Q^2 - 2Q^2 - Q^2e^{-2ika} - Q^2e^{2ika}}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m_Am_B\omega^4 - 2Q\left(m_A + m_B\right)\omega^2 + 4Q^2 - 2Q^2 - Q^2e^{-2ika} - Q^2e^{2ika}}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m_Am_B\omega^4 - 2Q(m_A + m_B)\omega^2 + 4Q^2 - 4Q^2cos^2\left(ka\right)}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m_Am_B\omega^4 - 2Q(m_A + m_B)\omega^2 + 4Q^2sin^2\left(ka\right)}

Note the difference of the argument of the sin function. This is the major change in the derivation of these two methods.

Then solving for omega squared:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega^2 = \frac{2Q(m_A+m_B)\pm\sqrt{4Q^2(m_A+m_B)^2-4m_Am_B(4Q^2sin^2(ka))} }{2m_Am_B} \;}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega^2 = Q({1 \over m_B} + {1 \over m_A}) \pm Q\sqrt{( {1 \over m_B}+ {1 \over m_A})^2 - {4 \over m_A m_B} sin^2(ka)}}

From here one can find the two branches of the frequency.

Acoustical: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega_A^2 = Q({1 \over m_B} + {1 \over m_A}) + Q\sqrt{( {1 \over m_B}+ {1 \over m_A})^2 - {4 \over m_A m_B} sin^2(ka)}}

With individual frequencies Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega_A = \pm \sqrt{Q({1 \over m_B} + {1 \over m_A}) + Q\sqrt{( {1 \over m_B}+ {1 \over m_A})^2 - {4 \over m_A m_B} sin^2(ka)}}}

And Optical: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega_O^2 = Q({1 \over m_B} + {1 \over m_A}) - Q\sqrt{( {1 \over m_B}+ {1 \over m_A})^2 - {4 \over m_A m_B} sin^2(ka)}}

With individual frequencies Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega_O = \pm \sqrt{Q({1 \over m_B} + {1 \over m_A}) - Q\sqrt{( {1 \over m_B}+ {1 \over m_A})^2 - {4 \over m_A m_B} sin^2(ka)}}}

Problem 2

Determine the speed of sound for this chain.

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega _{\alpha }(k)\approx C_{\alpha } k \;}

where

  • Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega_{\alpha } \;} = frequency
  • Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C_{\alpha } \;} = speed of sound

Therefore the speed of sound:

What is the lowest frequency of long-wavelength sound corresponding to the optical branch?

Problem 3

Sketch the motion of the atoms corresponding to the edge of the Brillouin zone, both for the optical and the acoustic branch.

Dispersionbranches.jpg

  • Acoustic Branch: lower branch
  • Optical Branch: upper branch, as on this branch the vibrations of the 2 types of atom are in antiphase and the resulting charge oscillation in an ionic craystal give a strong coupling to electromagnetic waves at the frequency of point A.

Problem 4

Determine the Debye temperature for this system, and determine the form of the specific heat in the limits of high and low temperatures.

Debye Temperature Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_D \;}

The Debye temperature, aka the effective sonic velocity, is a measure of the hardness of the crystal

From our class lectures:

or

The Debye Frequency is defined as

where is the speed of sound defined above.

Considering the fact that this is a one-dimensional system, the Debye Frequency is going to be slightly different.

is the frequency for the one-dimensional case.

Specific Heat

Specific Heat in a solid is defined as

where U is the total energy of the system, and T is the temperature of the system.

We know that the energy of a phonon system is

And the total energy according to the Bose-Einstein Distribution is

For the one-dimensional case, making the integral depend on n.

Substituting in the equation

and

We are left with the following Equation:

Now this is hard to solve overall for, but an approximation can be found for low temperatures and high temperatures.


Low Temperature Limit

We have the integral:

And on low temperatures, much smaller than the Debye temperature it is as if the upper limit is infinite. We can use the substitution for the integral:

Substituting that into the equation for the Energy, we are left with

and our Specific heat is now


High Temperature Limit

We have the integral:

which can not be solved analytically. However, at high temperatures above the Debye Temperature, the value of x is very small and we can use the approximation that .

Which leaves us with the (much easier to solve) integral of

Which reduces to

Then the specific heat is equal to

Problem 5

Consider low temperatures () and determine the wavelength of the most abundant phonons

Given

  • Bose-Einstein Distribution
    • Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(E) \;} = probability that a particle will have energy E
    • = Boltzmann constant
    • = Temperature
  • Planck's Radiation Formula
    • Density by frequency:
    • Density by wavelength:
  • Wien's law
    • is the peak wavelength in meters,
    • = temperature of the blackbody in Kelvin
    • = Wien's displacement constant

Planck's Radiation Formula

Take the derivative and set = 0 to find the maximum

Retrieved from "http://wiki.physics.fsu.edu/index.php?title=Solution_to_Set_5&oldid=3190"