Solution to Set 6: Difference between revisions
(Begin) |
|||
| (33 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
==Problem 1.== | ==Problem 1== | ||
===Given=== | |||
''Aluminum''(Al) is trivalent with | |||
* atomic mass <math>m_{a} = 27</math> amu | |||
* density <math>n = 2.7 g/cm^3</math> | |||
* room temperature <math>T = 293 - 296.5 K</math> | |||
* mean free time between electron collisions <math>t_{avg} = 4{\rm x}10^{-14}</math> s. | |||
===(a) Resistivity === | |||
Calculate the resistivity <math>\rho</math> of aluminum(Al) at room temperature. | |||
<math>\rho = \frac{1}{\sigma} \;</math> | |||
<math> = \frac{1}{ 37.8 \times 10^{6} S m^{-1}} \;</math> | |||
<math> = 2.82 \times 10^{-8} \;</math>Ω·m | |||
===(b) Current === | |||
[[Image:wire cross section.gif|left|150px]] | |||
If a 2-V voltage is applied to the ends of an aluminum wire 10 m long and with a cross- sectional area of <math>1 mm^2</math> | |||
<math>R = \frac{\ell \cdot \rho}{A} \;</math> | |||
<math> = \frac{\left (10m \right ) \cdot \left (2.646 \times 10^{-8} \Omega \cdot m \right )}{\left (10^{-6}m \right )} \;</math> | |||
<math> = 0.2646 \Omega \;</math> | |||
What is the current flowing through it? | |||
<math>I = \frac{V}{R} = \frac{2V}{0.2646 \Omega} = 7.559 A \;</math> | |||
==Problem 2== | ==Problem 2== | ||
The resistivity of a certain material at room temperature is 0.02 Wm and the Hall coefficient is <math>5{\rm x}10^{-4}</math> <math>m^3 /C</math>. An electric field of 1 V/m is applied across it. Deduce all the information you can think of about this material. | The resistivity of a certain material at room temperature is 0.02 Wm and the Hall coefficient is <math>5{\rm x}10^{-4}</math> <math>m^3 /C</math>. An electric field of 1 V/m is applied across it. Deduce all the information you can think of about this material. | ||
===Given=== | |||
* Temperature <math>T = 20^{\circ} C \;</math> | |||
* Resistivity <math>\rho = 0.02 \Omega \cdot m \;</math> | |||
* Hall coefficient <math>R_{H} = 5{\rm x}10^{-4} \tfrac{m^{3}}{C} \;</math> | |||
* Electric field <math>E = 1 \tfrac{V}{m} \;</math> | |||
===Deduction=== | |||
[[Image:Detective.gif|right|250px]] | |||
* Conductivity | |||
<math>\sigma = \frac{1}{\rho} = \frac{1}{0.02 \Omega \cdot m} = 50 \tfrac{S}{m} \;</math> | |||
* Current Density | |||
<math>\mathbf{J} = \frac{E}{\rho} = \frac{1 \tfrac{V}{m}}{0.02 \Omega \cdot m} = 50 \tfrac {A}{m^{2}} \;</math> | |||
* Magnetic Field | |||
<math>R_{H} = \frac{E}{\mathbf{J} \cdot B} \;</math> | |||
<math>B = \frac{E}{\mathbf{J} \cdot R_{H}} \;</math> | |||
<math> = \frac{\left (1 \tfrac{V}{m} \right )}{\left ( 50 \tfrac{A}{m^{2}} \right ) \left ( 5 \times 10^{-4} m^3 \right )} \;</math> | |||
<math> = 40 T \;</math> | |||
==Problem 3.== | ==Problem 3.== | ||
a) Sketch | ===(a) Hall Effect Sketch=== | ||
Sketch a setup used to measure the Hall effect. Label each part. | |||
[[Image:Hall_Effect.jpg|center|frameless|400px]] | |||
===(b) Semiconductor Crystal=== | |||
A semiconductor crystal is 5 mm long, 4 mm wide, and 2 mm thick. A 40mA current flows across the length of the sample after a 2-V battery is connected to the ends. When a 0.1T magnetic field is applied perpendicular to the large surface of the specimen, a Hall voltage of 15mV develops across the width of the sample. | |||
====Given==== | |||
* Length <math>\ell</math> = 5 mm = 0.005 m | |||
* Width W = 4 mm = 0.004 m | |||
* Thickness H = 2 mm = 0.002 m | |||
* Current I = 40 mA = 0.04 A | |||
* Voltage V = 2 V | |||
* Mag Field B = 0.1 T | |||
* Hall Volt <math>V_H</math> = 15 mV = 0.015 V | |||
You can deduce that: | |||
* Area <math>A = L \times W = 2.0 \times 10^{-5} m^2</math> | |||
[[Image:Semiconductor.png|right|200px]] | |||
====Determine==== | |||
* Conductivity | |||
<math>\rho = R \cdot \frac {A}{\ell} \;</math> | |||
<math> = \frac{V}{I} \cdot \frac {A}{\ell} \;</math> | |||
<math> = \frac{2V}{0.04A} \cdot \frac{2 \times 10^{-5}m^2}{0.005m} \;</math> | |||
<math> = 0.2 \Omega \cdot m \;</math> | |||
<math>\sigma = \frac{1}{\rho} = \frac{1}{0.2 \Omega \cdot m} \;</math> | |||
<math> = 5 \tfrac{S}{m} \;</math> | |||
* Carrier density | |||
<math>R_H = \frac{E_y}{\mathbf{J_x} \cdot B} \;</math> | |||
<math> = \frac{V_H}{I \cdot \tfrac{B}{\ell}} \;</math> | |||
<math> = -\frac{1}{ne} \;</math> | |||
<math>n = -\frac{1}{e} \cdot \frac{I \cdot \tfrac{B}{\ell}}{V_H} \;</math> | |||
<math> = - \frac{1}{-1.602 \times 10^{-19}C} \cdot \frac{\left (0.04A \right ) \cdot \tfrac{\left (0.1T \right )}{\left (0.005m \right )}}{0.015V} \;</math> | |||
<math> = 3.329 \times 10^{20} m^{-3} \;</math> | |||
* Mobility | |||
<math>\mathbf{E} = \frac{1}{4 \pi \varepsilon_0 } \int \frac{\rho}{r^2} \mathbf{\hat{r}} dV \;</math> | |||
<math> = \frac{1}{4 \pi \left (8.854 \times 10^{-12} \tfrac{C^2}{N \cdot m^2} \right )} \int \frac{\left ( 0.2 \Omega \cdot m \right )}{\left ( 0.005m \right )^2} dV \;</math> | |||
<math> = 3.595 \times 10^{11} \tfrac{N}{C} \;</math> | |||
<math>\mathbf{F} = q \cdot \mathbf{E} \;</math> | |||
<math> = \left ( 1.602 \times 10^{-19} C \right ) \left ( 3.595 \times 10^{11} \tfrac{N}{C} \right ) \;</math> | |||
<math> = 5.759 \times 10^{-8} N \;</math> | |||
* Fermi velocity | |||
<math>E_f = \frac{\hbar^2 \pi^2}{2 m_e \ell^2} n_f^2 \;</math> | |||
<math> = \frac{\left (1.055 \times 10^{-34} J \cdot s \right )^2 \pi^2}{2 \cdot \left ( 9.109 \times 10^{-31} kg \right ) \left ( 0.005m \right )^2} \;</math> | |||
<math> = 2.412 \times 10^{-33} J \;</math> | |||
<math>V_f = \sqrt{\frac{2 E_f}{m_e}} \;</math> | |||
<math> = \sqrt{\frac{2 \left ( 2.412 \times 10^{-33} J \right ) }{\left ( 9.109 \times 10^{-31} kg \right )}} \;</math> | |||
<math> = 0.0727715501 \tfrac{m}{s} \;</math> | |||
==Problem 4== | ==Problem 4== | ||
a) Derive the expressions for the Fermi energy, Fermi velocity, and electronic density of states for a two-dimensional free electron gas. | ===(a) Fermi Derivations=== | ||
Derive the expressions for the Fermi energy, Fermi velocity, and electronic density of states for a two-dimensional free electron gas. | |||
====Fermi Energy==== | |||
<math>E_f = \frac{\hbar^2 \pi^2}{2 m_e \ell^2} n_f^2 \;</math> | |||
====Fermi Velocity==== | |||
Fermi energy is related to fermi velocity such that: | |||
:<math>E_F = \tfrac{1}{2}m_e v_F^2 \;</math> | |||
Solve for velocity | |||
:<math>v_F = \sqrt{\frac{2 E_F}{m_e}} \;</math> | |||
====Electronic Density==== | |||
In 1 dimension | |||
::''<math>E(k) = \frac{\hbar^2 k^2}{2m}</math>'' | |||
::''<math>k = \frac{2\pi m}{L}\;</math>; <math>m = 0, \pm 1, \pm 2,...</math>'' | |||
::''<math>n = \frac{N}{L} = \frac{2}{L} \sum_{k < |k_F |} = \frac{2}{2 \pi } \sum_{k < |k_F |}\frac{2 \pi}{L} = \frac{2}{2 \pi} 2\int_0^{k_F} dk = \frac{2k_F}{\pi}.</math> | |||
::''Here the extra factor of 2 is due to spin'' | |||
::''The other factor of two comes from the addition of the negative values for k'' | |||
::''<math>E_F = \frac{\hbar^2 \pi^2 n^2}{8m}.</math>'' | |||
===(b) Fermi Energy & Velocity of 2D Gas === | |||
A 2D electron gas formed in a GaAs/AlGaAs quantum well has a density of <math>2{\rm x}10^{11} cm^{-2}</math>. Assuming that the electrons there have the free electron mass, calculate the Fermi energy and Fermi velocity. | |||
<math>2{\rm x}10^{11} cm^{-2}</math>. Assuming that the electrons there have the free electron mass, calculate the | |||
Fermi energy and Fermi velocity. | |||
Latest revision as of 19:49, 28 April 2009
Problem 1
Given
Aluminum(Al) is trivalent with
- atomic mass Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m_{a} = 27} amu
- density Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n = 2.7 g/cm^3}
- room temperature Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T = 293 - 296.5 K}
- mean free time between electron collisions Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t_{avg} = 4{\rm x}10^{-14}} s.
(a) Resistivity
Calculate the resistivity Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho} of aluminum(Al) at room temperature.
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho = \frac{1}{\sigma} \;} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = \frac{1}{ 37.8 \times 10^{6} S m^{-1}} \;} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = 2.82 \times 10^{-8} \;} Ω·m
(b) Current
If a 2-V voltage is applied to the ends of an aluminum wire 10 m long and with a cross- sectional area of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1 mm^2}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle R = \frac{\ell \cdot \rho}{A} \;} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = \frac{\left (10m \right ) \cdot \left (2.646 \times 10^{-8} \Omega \cdot m \right )}{\left (10^{-6}m \right )} \;} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = 0.2646 \Omega \;}
What is the current flowing through it?
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I = \frac{V}{R} = \frac{2V}{0.2646 \Omega} = 7.559 A \;}
Problem 2
The resistivity of a certain material at room temperature is 0.02 Wm and the Hall coefficient is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 5{\rm x}10^{-4}} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m^3 /C} . An electric field of 1 V/m is applied across it. Deduce all the information you can think of about this material.
Given
- Temperature Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T = 20^{\circ} C \;}
- Resistivity Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho = 0.02 \Omega \cdot m \;}
- Hall coefficient Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle R_{H} = 5{\rm x}10^{-4} \tfrac{m^{3}}{C} \;}
- Electric field Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E = 1 \tfrac{V}{m} \;}
Deduction
- Conductivity
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma = \frac{1}{\rho} = \frac{1}{0.02 \Omega \cdot m} = 50 \tfrac{S}{m} \;}
- Current Density
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{J} = \frac{E}{\rho} = \frac{1 \tfrac{V}{m}}{0.02 \Omega \cdot m} = 50 \tfrac {A}{m^{2}} \;}
- Magnetic Field
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle R_{H} = \frac{E}{\mathbf{J} \cdot B} \;}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B = \frac{E}{\mathbf{J} \cdot R_{H}} \;} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = \frac{\left (1 \tfrac{V}{m} \right )}{\left ( 50 \tfrac{A}{m^{2}} \right ) \left ( 5 \times 10^{-4} m^3 \right )} \;} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = 40 T \;}
Problem 3.
(a) Hall Effect Sketch
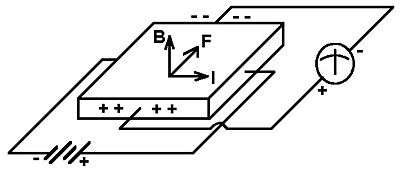
Sketch a setup used to measure the Hall effect. Label each part.
(b) Semiconductor Crystal
A semiconductor crystal is 5 mm long, 4 mm wide, and 2 mm thick. A 40mA current flows across the length of the sample after a 2-V battery is connected to the ends. When a 0.1T magnetic field is applied perpendicular to the large surface of the specimen, a Hall voltage of 15mV develops across the width of the sample.
Given
- Length Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ell} = 5 mm = 0.005 m
- Width W = 4 mm = 0.004 m
- Thickness H = 2 mm = 0.002 m
- Current I = 40 mA = 0.04 A
- Voltage V = 2 V
- Mag Field B = 0.1 T
- Hall Volt Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_H} = 15 mV = 0.015 V
You can deduce that:
- Area Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A = L \times W = 2.0 \times 10^{-5} m^2}
Determine
- Conductivity
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho = R \cdot \frac {A}{\ell} \;} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = \frac{V}{I} \cdot \frac {A}{\ell} \;} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = \frac{2V}{0.04A} \cdot \frac{2 \times 10^{-5}m^2}{0.005m} \;} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = 0.2 \Omega \cdot m \;}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma = \frac{1}{\rho} = \frac{1}{0.2 \Omega \cdot m} \;} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = 5 \tfrac{S}{m} \;}
- Carrier density
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle R_H = \frac{E_y}{\mathbf{J_x} \cdot B} \;} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = \frac{V_H}{I \cdot \tfrac{B}{\ell}} \;} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = -\frac{1}{ne} \;}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n = -\frac{1}{e} \cdot \frac{I \cdot \tfrac{B}{\ell}}{V_H} \;} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = - \frac{1}{-1.602 \times 10^{-19}C} \cdot \frac{\left (0.04A \right ) \cdot \tfrac{\left (0.1T \right )}{\left (0.005m \right )}}{0.015V} \;} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = 3.329 \times 10^{20} m^{-3} \;}
- Mobility
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{E} = \frac{1}{4 \pi \varepsilon_0 } \int \frac{\rho}{r^2} \mathbf{\hat{r}} dV \;} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = \frac{1}{4 \pi \left (8.854 \times 10^{-12} \tfrac{C^2}{N \cdot m^2} \right )} \int \frac{\left ( 0.2 \Omega \cdot m \right )}{\left ( 0.005m \right )^2} dV \;} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = 3.595 \times 10^{11} \tfrac{N}{C} \;}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{F} = q \cdot \mathbf{E} \;} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = \left ( 1.602 \times 10^{-19} C \right ) \left ( 3.595 \times 10^{11} \tfrac{N}{C} \right ) \;} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = 5.759 \times 10^{-8} N \;}
- Fermi velocity
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_f = \frac{\hbar^2 \pi^2}{2 m_e \ell^2} n_f^2 \;} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = \frac{\left (1.055 \times 10^{-34} J \cdot s \right )^2 \pi^2}{2 \cdot \left ( 9.109 \times 10^{-31} kg \right ) \left ( 0.005m \right )^2} \;} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = 2.412 \times 10^{-33} J \;}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_f = \sqrt{\frac{2 E_f}{m_e}} \;}
Problem 4
(a) Fermi Derivations
Derive the expressions for the Fermi energy, Fermi velocity, and electronic density of states for a two-dimensional free electron gas.
Fermi Energy
Fermi Velocity
Fermi energy is related to fermi velocity such that:
Solve for velocity
Electronic Density
In 1 dimension
- ;
- Here the extra factor of 2 is due to spin
- The other factor of two comes from the addition of the negative values for k
(b) Fermi Energy & Velocity of 2D Gas
A 2D electron gas formed in a GaAs/AlGaAs quantum well has a density of . Assuming that the electrons there have the free electron mass, calculate the Fermi energy and Fermi velocity.
