Liquid Crystals: Difference between revisions
SohamGhosh (talk | contribs) (New page: == Introduction == Homogeneous, isotropic liquids have an average structure that is invariant under arbitrary rotations and translations.It has no long range order, and has the highest po...) |
SohamGhosh (talk | contribs) |
||
| (59 intermediate revisions by 3 users not shown) | |||
| Line 3: | Line 3: | ||
Homogeneous, isotropic liquids have an average structure that is invariant under arbitrary rotations and translations.It has no long range order, and has the highest possible symmetry with maximum possible entropy.The crystalline state has long range translational and rotational order, with the lowest possible symmetry consistent with a regular filling of space. Between these two, there are systems which exhibit short range correlations in some directions and long range in others, and have symmetries intermediate between between those of liquids and crystals. | Homogeneous, isotropic liquids have an average structure that is invariant under arbitrary rotations and translations.It has no long range order, and has the highest possible symmetry with maximum possible entropy.The crystalline state has long range translational and rotational order, with the lowest possible symmetry consistent with a regular filling of space. Between these two, there are systems which exhibit short range correlations in some directions and long range in others, and have symmetries intermediate between between those of liquids and crystals. | ||
Among the materials that show intermediate order, the most widely studied are liquid crystals | [[Image:lc1.jpg]] [[Image:lc2.gif]] | ||
Among the materials that show intermediate order, the most widely studied are liquid crystals.Liquid crystals are usually made of strongly anisotropic organic molecules, either elongated (calamitic, rod-like molecules) or disk-like (discotic molecules). As a rule, the inner part of mesogenic molecules is rigid (e.g. phenyl groups) and the outer part flexible (aliphatic chains). This double character explains altogether the existence of steric interactions (between rod-like or disk-like cores) yielding orientational order and the fluidity of the mesomorphic phases. Typical examples are cyanobiphenyls and MBBA. These produce thermotropic mesophases,i.e. phases with a single component, whose phase transitions can be induced by a change in temperature.The other broad LC class is constituted by the lyotropic mesophases: they occur when anisotropic amphiphilic molecules (soaps, phospholipids, various types of surfactant molecules and biomolecules) are added to a solvent. Because amphiphiles have two distinct parts, a polar head and a non-polar tail,the building units of lyotropic phases are usually aggregates of many molecules(micelles) rather than single molecules. This microphase separation dominating the lyotropic behavior is partly present also in thermotropic LC, as for example in the smectic phases, where polar and non polar portions of the molecules form distinct alternatinig planes in the system.A typical example of lyotropics is a water solution of SDS, sodium dodecyl sulphate. For concentrations above the critical micellar concentration, cmc, these molecules form aggregates of different shapes, spherical or cylindrical micelles,bilayers, inverse cylinders, and inverse micelles.'''[1,2.3]''' | |||
[[Image:lc3.jpg]] | |||
== Classification of LC phases == | |||
LCs show many possible structures, which can belong to the same compound (polymorphism). There are four basic types of liquid crystalline phases, classified accordingly to the dimensionality of the translational correlations of building units: nematic (no translational correlations), smectic (1D correlation),columnar (2D) and various 3D-correlated structures, such as cubic phases. | |||
=== Density Correlation and Structure Factor === | |||
A lot of information about the bulk structure of LCs can be obtained via scattering of X-rays. let <math>|\boldsymbol{k}\rangle</math> and <math>|\boldsymbol{k}^{'}\rangle</math> be the incident and final plane wave state of the scattered particle with respective momenta <math>\hbar\boldsymbol{k}</math> and <math>\hbar\boldsymbol{k}^{'}</math> If the scattered particle interacts weakly with the scaterring medium via a sufficiently short-ranged interaction <math>U</math>, then by Fermi's Golden rule, the transition rate between <math>|\boldsymbol{k}\rangle</math> and <math>|\boldsymbol{k}^{'}\rangle</math> is proportional to the square of the matrix element, | |||
<math>M_{\boldsymbol{k},\boldsymbol{k^{'}}} = \langle\boldsymbol{k}|U|\boldsymbol{k^{'}}\rangle = \int d^{d}x e^{-i\boldsymbol{k}.\boldsymbol{x}}U(\boldsymbol{x})e^{i\boldsymbol{k^{'}}.\boldsymbol{x}} </math> | |||
where <math>U(\boldsymbol{x})</math> is the scattering potential in the coordinate representation of the scattered particle, and our plane wave states are unnormalized. | |||
In multiparticle systems, the scattering potential is the sum of terms from individual atoms in the material: | |||
\alpha<math>U(\boldsymbol{x}) = \sum_{\alpha} U_{\alpha}(\boldsymbol{x}-\boldsymbol{x_{'}})</math> | |||
where <math>\boldsymbol{x_{\alpha}}</math> is the position of the atom labeled <math>\alpha</math>. the matrix element, therefore, is | |||
<math>\langle\boldsymbol{k}|U|\boldsymbol{k^{'}}\rangle = \sum_{\alpha}\int d^{d}x e^{-i\boldsymbol{k}.\boldsymbol{x}}U_{\alpha}(\boldsymbol{x}-\boldsymbol{x_{\alpha}})e^{i\boldsymbol{k^{'}}.\boldsymbol{x}}</math> | |||
To seperate the potential interaction and the interatomic correlation factors, we shift our centers to each <math>x_{\alpha}</math>. Let <math>\boldsymbol{R}_{\alpha} = \boldsymbol{x}-\boldsymbol{x_{\alpha}}</math>. | |||
<math>\langle\boldsymbol{k}|U|\boldsymbol{k^{'}}\rangle = \sum_{\alpha}\int d^{d}R_{\alpha} e^{-i\boldsymbol{k}.(\boldsymbol{x}_{\alpha}+\boldsymbol{R}_{\alpha})}U_{\alpha}(\boldsymbol{R}_{\alpha})e^{i\boldsymbol{k^{'}}.(\boldsymbol{x}_{\alpha}+\boldsymbol{R}_{\alpha})} </math> | |||
<math>= \sum_{\alpha}[\int d^{d}R_{\alpha} e^{-i\boldsymbol{q}.\boldsymbol{R}_{\alpha}}U_{\alpha}(\boldsymbol{R}_{\alpha})]e^{-i\boldsymbol{q}.\boldsymbol{x}_{\alpha}}</math> | |||
<math>=\sum_{\alpha}U_{\alpha}(\boldsymbol{q})e^{-i\boldsymbol{q}.\boldsymbol{x}_{\alpha}}</math> | |||
Here the scattering wave vector is <math>\boldsymbol{q} = \boldsymbol{k} - \boldsymbol{k}^{'}</math> and <math>U_{\alpha}(\boldsymbol{q})</math> is the atomic form factor, which is nothing but the Fourier transform of the atomic potential. The differential cross-section is proportional to the matrix element squared: | |||
<math>|\langle\boldsymbol{k}|U|\boldsymbol{k^{'}}\rangle|^{2} = \sum_{\alpha,\alpha^{'}}U_{\alpha}(\boldsymbol{q})U_{\alpha^{'}}^{*}(\boldsymbol{q})e^{-i\boldsymbol{q}.\boldsymbol{x}_{\alpha}}e^{i\boldsymbol{q}.\boldsymbol{x}_{\alpha^{'}}}</math> | |||
If the positions of atoms are rigidly fixed,then this expression gives the exact answer. However, in real materials, the particles move around,probing large regions of phase space consistent with statistical mechanics, and we need an ensemble average of the ideal cross-section. Under ergodic hypothesis and assuming the particles are identical, | |||
<math>\frac{\mathrm{d}^{2}\sigma }{\mathrm{d} \Omega}\sim |U_{\alpha}(\boldsymbol{q})|^{2}\boldsymbol{I}(\boldsymbol{q})</math> | |||
where the function | |||
<math>\boldsymbol{I}(\boldsymbol{q}) = \left \langle\sum_{\alpha,\alpha^{'}}e^{-i\boldsymbol{q}.(\boldsymbol{x}_{\alpha}-\boldsymbol{x_{\alpha^{'}}})}\right \rangle</math> | |||
is called the structure function. As intensive version of the structure function is called the structure factor. | |||
<math>S(\boldsymbol{q}) = \frac{\boldsymbol{I}(\boldsymbol{q})}{N} </math> or <math>S(\boldsymbol{q}) = \frac{\boldsymbol{I}(\boldsymbol{q})}{V}</math> | |||
====Two point density correlation function and its relation with the structure factor==== | |||
The number density operator is defined as | |||
<math>n(\boldsymbol{x}) = \sum_{\alpha}\delta(\boldsymbol{x}-\boldsymbol{x}_{\alpha})</math> | |||
The two point density density correlation function is defined as | |||
<math>C_{nn}(\boldsymbol{x}_{1},\boldsymbol{x}_{2}) = \left \langle n(\boldsymbol{x}_{1})n(\boldsymbol{x}_{2})\right \rangle</math> | |||
) | |||
<math>=\left \langle \sum_{\alpha,\alpha^{'}}\delta(\boldsymbol{x}_{1}-\boldsymbol{x}_{\alpha})\delta(\boldsymbol{x}_{2}-\boldsymbol{x}_{\alpha^{'}})\right \rangle</math> | |||
The structure function is simply a Fourier transform of this function: | |||
<math>\boldsymbol{I}(\boldsymbol{q})= \left \langle n(\boldsymbol{q})n(-\boldsymbol{q})\right \rangle</math> | |||
where | |||
<math>n(\boldsymbol{q}) = \int d^{d}x e^{-i\boldsymbol{k}.\boldsymbol{x}}n(\boldsymbol{x}) = \sum_{\alpha}e^{-i\boldsymbol{k}.\boldsymbol{x}}</math> is the Fourier transform of the density. | |||
In a statistical ensemble, | |||
<math>\left \langle n(\boldsymbol{q})\right \rangle = \int d^{d}x e^{-i\boldsymbol{k}.\boldsymbol{x}}\left \langle n(\boldsymbol{x})\right \rangle = \left \langle\sum_{\alpha}e^{-i\boldsymbol{k}.\boldsymbol{x}} \right \rangle</math> | |||
So scattering measures density-density correlation. | |||
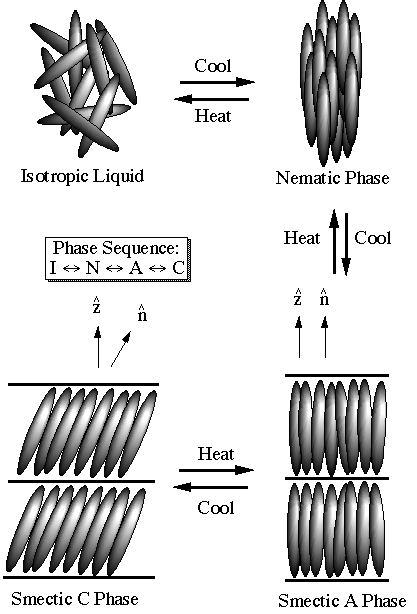
===Isotropic, nematic and cholesteric phases[4] === | |||
[[Image:lc4.gif]] | |||
In isotropic liquids, | |||
<math>\left \langle n(\boldsymbol{x})\right \rangle = \left \langle n \right \rangle</math>, a constant, so | |||
<math>\left \langle n(\boldsymbol{q})\right \rangle = V \left \langle n \right \rangle \delta _{q,0} </math> is nonzero only for <math>\boldsymbol{q} = 0</math>, and there is a contribution to the structure factor only for forward scattering. | |||
In a regularly periodic crystal, | |||
<math>\left \langle n(\boldsymbol{x})\right \rangle = \sum_{\boldsymbol{G}}\left \langle n_{\boldsymbol{G}} \right \rangle e^{-i\boldsymbol{G}.\boldsymbol{x}}</math> | |||
So there is a peak corresponding to each wavevector <math>\boldsymbol{G}</math> in the reciprocal space. | |||
In an Isotropic LCD, the structure factor is isotropic, but shows liquid-like rings at wave numbers corresponding to the two characteristic lengths of the individual molecules-their length ''l'' and diameter ''a''. | |||
When the isotropic liquid is cooled, the first phase rhat condenses in the ''nematic (N)''phase in which long molecules align so that they are on an average parallel to a particular direction specified by a unit vector <math>\boldsymbol{n}</math> called the ''director''The positions of the molecular centers of mass remains randomly distributed, like in an isotropic fluid. So the nematic phase breaks rotational invariance but maintains translational invariance. It is easy to visualize that in a statistical ensemble, rotations about <math>\boldsymbol{n}</math> leaves the phase unchanged, while rotation in a plane perpendicular to <math>\boldsymbol{n}</math> does not. The number density of the nematic phase has two peaks. The structure factor of the nematic phase is axially symmetric in any phase perpendicular to <math>\boldsymbol{n}</math> but has only two-fold symmetry in any plane containing <math>\boldsymbol{n}</math>. Two possible forms for the X-ray intensity can result. In the first there are diffuse spots at <math>\boldsymbol{q}=q_{0}\boldsymbol{n}</math> with <math>q_{0} = 2\pi/l</math>, and in the second there are diffuse rings cetered at the same values of ''q''. | |||
===Smectics-A and -C=== | |||
As temperature is further reduced, molecules begin to segregate into planes giving rise to a smectic-A (Sm-y4) liquid crystal. The usual picture of this smectic phase is one with molecules situated in well-defined layers with a spacing that is essentially the rod length. There is liquid-like motion of the rods in | |||
each layer and no correlation of the positions of the molecules from one layer to the next. In smectic-,4 liquid crystals, molecules are aligned perpendicular to the | |||
layers. The introduction of the layering indicates the presence of a mass density wave perpendicular to the layers. There is, therefore, positional correlation in | |||
the system which can be described as a sinusoidal modulation of the average molecular number-density, | |||
<math>\left \langle n(\boldsymbol{x})\right \rangle = n_{0} + 2n_{q_{0}}\cos({q_0}z)</math> | |||
where the z-axis is along the layer normals and parallel to <math>\boldsymbol{n}</math>. From this, we get | |||
<math>S(\boldsymbol{q}) = |\left \langle n_{q_{0}}\right \rangle|^{2}(2\pi)^{3}[\delta(\boldsymbol{q}_{z} - q_{0}\boldsymbol{e}_{z}) + \delta(\boldsymbol{q}_{z}+q_{0}\boldsymbol{e}_{z})]</math> | |||
In some systems, molecules align along an axis tilted relative to the smectic planes. This is the smectic-C phase. It has a lower symmetry than the smectic-,4 phase because the tilted molecules pick out a special direction in the smectic plane, i.e., their projections in the xy-plane align,like the molecules in a nematic, along a common direction denoted by a unit vector <math>\boldsymbol{e}</math>, called the '''e'''-director. There are in fact transitions from the smectic-A to the smectic-C phase in which the tilt angle grows continuously from zero. The structure factor of the nematic phase just above a smectic-C phase has diffuse rings rather than diffuse spots. | |||
===Hexatic Phases=== | |||
When smectic-A phases are cooled, they condense into what was historically called a smectic-B phase. It is now known that a smectic-B phase can be a crystalline-B phase with a three-dimensional crystal structure and Bragg scattering at points in a three-dimensional reciprocal lattice. In some cases, however, the smectic-B phase is not a true crystal. It has hexagonal orientational order manifested by the development of a six-fold modulation in the intensity of the diffuse ring at q = 2n/a in the X-ray scattering intensity of the smectic-,4 phase. Whereas the smectic-,4 phase is invariant with respect to arbitrary rotations about <math>\boldsymbol{n}</math>,this hexatic-B phase is invariant only with respect to rotations of 2n/6 about <math>\boldsymbol{n}</math>. | |||
===Discotic and Columnar Phases=== | |||
The nematic and smectic phases just discussed are generally found in materials consisting of rod-like molecules. Plate-like rather than rod-like molecules can form discotic nematic phases, in which the plate normals are aligned, as well as phases with crystalline order in two dimensions and liquid-like order in the third direction. The latter are called columnar. The plate-like molecules segregate into columns with the plate normals either parallel to or tilted at an angle to the columnar axes. There is no long-range positional order within a column. The columns themselves form any of the two-dimensional crystals. | |||
==The First Order Nematic-to-Isotropic Transition== | |||
Suppose that the liquid crystal is composed of rod-like molecules in which (i) the distribution function is cylindrically symmetric about the axis of preferred orientation n and (ii) the directions <math>\boldsymbol{n}</math> and <math>-\boldsymbol{n}</math> are fully equivalent, i.e., the preferred axis is non-polar. Subject to these two symmetry properties, and assuming the rods to be cylindrically symmetric, the simplest way of defining the degree of alignment is by the parameter s, first introduced by | |||
Tsvetkov[5] | |||
<math>S = \frac{1}{3}\left \langle 3\cos^{2}\theta -1\right \rangle</math> | |||
where <math>\theta</math> is the angle which the long molecular axis makes with <math>\boldsymbol{n}</math>. For perfectly parallel alignment <math>s=1</math>, while for random orientations <math>s = 0</math> | |||
The next task is to create an order parameter. Although it is tempting to associate the order parameter with an unit vector <math>\nu^{\alpha}</math>along the long axis direction of molecule <math>\alpha</math> located at <math>\boldsymbol{x}^{\alpha}</math>.However, we note that a rotation by <math>\pi</math> leaves the phase unchanged, and so the order prameter must be an even function of <math>\nu^{\alpha}</math>. So we look for the next option, which is a symmetric traceless tensor, which, as needed, yields zero when averaged over all directions | |||
<math>Q_{ij} = \frac{V}{N}\sum_{\alpha}(\nu_{i}^{\alpha}\nu_{j}^{\beta} -\frac{1}{3}\delta_{ij})\delta(\boldsymbol{x} - \boldsymbol{x}^{\alpha})</math> | |||
<math>\left \langle Q \right \rangle= S(n_{i}n_{j}-\frac{1}{3}\delta_{ij}) </math> | |||
Where the unit vector '''n''' is the Frank director, and | |||
<math>S = \frac{1}{3}\left \langle (3\cos\theta^{\alpha} -1)\right \rangle</math> where <math>theta^{\alpha}</math> is the angle between the molecular axis and the director '''n'''. | |||
Now the Landau free energy <math>f</math> must be invariant under all rotations. Since '''Q''' is a tensor, the only way, to the fourth order, is | |||
<math>f = Tr\left \langle Q \right \rangle\ + \frac{1}{2}r(\frac{3}{2}Tr\left \rangle Q \right \rangle^{2}) - w(\frac{9}{2}Tr\left \rangle Q \right \rangle^{3})+u(\frac{3}{2}Tr\left \rangle Q \right \rangle^{2})^{2}</math> | |||
Since '''Q''' is a traceless tensor, the first term is zero, so | |||
<math>f = \frac{1}{2}rS^{2} - wS^{3} + uS^{4}</math> | |||
We choose | |||
<math>r = a(T-T^{*})</math> | |||
w and u are temperature independent. | |||
Note the presence of the cubic term, which is a consequence of the quadrupolar symmetry of the molecules and the resultant tensor property of the order parameter. | |||
<math>f</math> is sketched as a function of <math>s</math> for various values of T in figure ??????.Note that the cubic term leads to an asymmetry in <math>f</math> as a function of S and the emergence of a secondary minimum at finite S. The value of <math>f</math>at this minimum is greater than zero at high temperature but becomes equal to zero at a critical temperature Tc that is greater than the temperature T* at which the extremum at the origin develops negative curvature. Since / is less than zero | |||
at the secondary minimum for all T < Tc, there is a phase transition with a discontinuous change in S at Tc, i.e. there is a first-order transition at Tc. T* is | |||
the limit of metastability of the isotropic phase since, for T* < T < Tc, the origin is still a local minimum even though it is not a global minimum. The limit of | |||
metastability of the nematic phase occurs at the temperature T" at which the secondary minimum disappears on heating. The first-order transition temperature Tc and the value Sc of S at Tc are calculated by requiring that / be an extremum with respect to S in equilibrium and that the free energies of the disordered and ordered phases be equal at the transition. The latter condition implies that the isotropic and nematic phases can coexist at the transition temperature. If other variables, such as pressure or density, were included in our treatment, the two phases would coexist along a line rather than at a single point. The equations determining Tc and Sc are, therefore, | |||
<math>\frac{\partial f}{\partial S} = (r-3wS+4uS^{2})S = 0</math> | |||
Thus, | |||
<math>S_{c} = \frac{w}{2u}</math>,<math>r_{c} = a(T_{c}-T^{*}) = \frac{w^{2}}{2u}</math> | |||
The transition being first order, there is an associated latent heat.heat. The entropy per unit volume of the disordered phase is zero in mean-field theory, whereas | |||
that of the nematic phase is negative. This result can be obtained from the freeenergy of the nematic phase, which to lowest order in <math>r-r_{c}</math> is | |||
<math>f = \frac{1}{2}(r-r_{c})\frac{w}{2u}^{2}</math> | |||
The entropy density relative to the isotropic phase is therefore | |||
<math>s = \frac{\partial f}{\partial T} = -\frac{1}{2}a\frac{w}{2u}^{2}</math> | |||
The latent heat absorbed in going from the nematic to the isotropic phase is | |||
<math>q = -T_{c}s = \frac{1}{2}aT_{c}\frac{w}{2u}^{2}</math> | |||
== Hydrodynamics of Liquid Crystals == | |||
===Basic introduction=== | |||
Thermodynamic equilibrium is produced and maintained by collisions between particles or elementary excitations that occur at a characteristic time interval math>\tau</math>. In classical fluids, <math>\tau</math> is of order <math>10^{-10}</math> to <math>10^{-14}</math> seconds. In low-temperature solids or in quantum liquids, <math>\tau</math> can be quite large, diverging as some inverse power of the temperature <math>T</math>. The mean distance A between collisions (mean free path) of particles or excitations is a characteristic velocity <math>v</math> times <math>\tau</math>. In fluids, <math>V</math> is determined by the kinetic energy, <math>v \sim (T/m)^{1/2}</math>, where <math>m</math> is a mass. In solids, <math>v</math> is typically a sound velocity. Imagine now a disturbance from the ideal equilibrium state that varies periodically in time and space with frequency <math>\omega</math> and wave number <math>q</math>. If <math>\omega\tau \ll 1</math> and <math>q\lambda \ll 1</math>, the disturbance varies slowly on time and length scales set by <math>\tau</math> and <math>\lambda</math>, and there will be many equilibrating collisions in each of its temporal and spatial cycles. Thus, each point in space is close to thermodynamic equilibrium at each instant of time, and one would expect to be able to treat such disturbances as perturbations from thermodynamic equilibrium even though they vary in time.Most disturbances in many body systems have characteristic frequencies that are of order <math>\tau^{-1}</math>. If excited, they decay rapidly to equilibrium. There are, however, certain classes of variables that are guaranteed to have slow temporal variations | |||
at long wavelengths. These are | |||
A) densities of conserved variables, and | |||
B) broken-symmetry elastic variables. | |||
A conserved density such as the number density n obeys a conservation law of the form | |||
<math>\frac{\partial n}{\partial t} + \nabla\cdot\mathbf{\boldsymbol{j}} = 0</math> | |||
where <math>\boldsymbol{j}</math> is the particle current.When Fourier transformed, such equations imply frequencies <math>\omega</math> that go to zero with wave number <math>q</math>. | |||
Out of our hydrodynamical analysis, we shall derive some important concepts, which are: | |||
• Long-wavelength, low-frequency excitations are associated with conservation laws and broken symmetry. | |||
• There is exactly one mode associated with each conservation law and each broken symmetry. | |||
• Currents of hydrodynamical variables contain reactive and dissipative parts.The reactive parts of currents couple variables of opposite sign under time reversal and lead to propagating modes. | |||
• In the absence of reactive couplings, the hydrodynamical modes are diffusive. | |||
• Diffusion constants are the ratio of a transport coefficient to a susceptibility. | |||
• The velocities of propagating modes are square roots of the ratio of a reactive transport coefficient to a susceptibility. | |||
===Hydrodynamics of Isotropic fluids=== | |||
====Conservation laws==== | |||
Due to the possibility of mass motion and possibility of relative motion of different parts of the fluid, there are conservation laws for mass <math>m</math> and momentum <math>p</math>in addition to that of energy, leading to five conserved hydrodynamical variables (2 for energy and mass, one each for each component of momentum) and five hydrodynamic modes. The respective density operators are | |||
<math>\hat{\varepsilon}(\boldsymbol{x},t) = \sum _{\alpha}\frac{(\boldsymbol{p}^{\alpha})^{2}}{2m} + \frac{1}{2}\sum_{\alpha \neq \beta}U(\boldsymbol{x}^{\alpha}-\boldsymbol{x}^{\beta})\delta(\boldsymbol{x}-\boldsymbol{x}^{\alpha})</math> | |||
<math>\hat{\rho}(\boldsymbol{x},t) = \sum_{\alpha}m\delta(\boldsymbol{x}-\boldsymbol{x}^{\alpha})</math> | |||
<math>\hat{\boldsymbol{g}}(\boldsymbol{x},t) = \sum_{\alpha}\boldsymbol{p}^{\alpha}\delta(\boldsymbol{x}-\boldsymbol{x}^{\alpha})</math> | |||
where <math>U(\boldsymbol{x})</math> is the two-body interaction potential.These densities obey local conservation laws | |||
<math>\frac{\partial \hat{\varepsilon}}{\partial t} + \nabla\cdot{\boldsymbol{j}^{\varepsilon}} = 0</math> | |||
<math>\frac{\partial \hat{\rho}}{\partial t} + \nabla\cdot{\hat{\boldsymbol{g}}} = 0</math> | |||
<math>\frac{\partial \hat{g_{i}}}{\partial t} + \nabla_{j}{\pi^{\varepsilon}_{ij}} = 0</math> | |||
where <math>\boldsymbol{j}^{\varepsilon}</math> is the energy current and <math>\pi^{\varepsilon}_{ij}</math> is the momentum current tensor.Note that the conserved | |||
momentum density is itself a current for another conserved density, the mass density.The conservation laws apply to averaged densities <math>\varepsilon(\boldsymbol{x},t) = \left \langle \hat{\varepsilon}(\boldsymbol{x},t) \right \rangle </math>, <math>\rho(\boldsymbol{x},t) = \left \langle \hat{\rho}(\boldsymbol{x},t) \right \rangle </math> and <math>\boldsymbol{g}(\boldsymbol{x},t) = \left \langle \hat{\boldsymbol{g}}(\boldsymbol{x},t) \right \rangle </math> as well as to other microscopic operators. Angular momentum is conserved but is not independent of <math>\boldsymbol{g}</math> | |||
====Thermodynamics==== | |||
The total Hamiltonian of this system is | |||
<math>H_{T} = H - \hat{P}\cdot{v}</math>, | |||
Where | |||
<math>\hat{P} = \sum_{\alpha}\boldsymbol{p}^{\alpha} = \int d^{d}x\hat{\boldsymbol{g}}(\boldsymbol{x},t) </math> is the total momentum operator and | |||
<math>H = \sum _{\alpha}\frac{(\boldsymbol{p}^{\alpha})^{2}}{2m} +U </math> | |||
the average of <math>H</math> is the internal energy <math>E</math>. The canonical partition function for a fluid with N particles in a volume V is then | |||
<math>Z(T,V,\boldsymbol{v}) = -Tre^{-\beta(H - \hat{P}\cdot{v})}</math> | |||
the thermodynamic potential, | |||
<math>F(T,V,N,\boldsymbol{v}) = -TlnZ_{N} = E - TS -\boldsymbol{P\cdot{v}}</math> | |||
satisfies | |||
<math>dF = -SdT-pdV+\mu dN-\boldsymbol{P\cdot{dv}}</math> | |||
We also get the entropy equation | |||
<math>Tds = d\varepsilon - \alpha d\rho - \boldsymbol{v\cdot{dg}}</math> | |||
====Constitutive relations from the entropy equation==== | |||
Using the entropy relation and the conservation laws, we get, | |||
<math>T\frac{\partial s}{\partial x} = \frac{\partial \varepsilon}{\partial t} - \alpha\frac{\partial\rho }{\partial t} - v_{j}\frac{\partial g_{j}}{\partial t}</math> | |||
We can write this as | |||
<math>T[\frac{\partial s}{\partial t} + \nabla \cdot{(\boldsymbol{v}s + \frac{1}{T}\boldsymbol{Q})}] = -\boldsymbol{Q}\cdot{(\nabla{T}/T)}-(\boldsymbol{g} - \rho \boldsymbol{v})\cdot \nabla \alpha - [\pi_{ji} - p\delta_{ij} -v_{i}g_{j}]\nabla_{i}v_{j}</math> | |||
Where <math>p</math> is the pressure derived from the thermodynamic potential and | |||
<math>Q_{i} = j^{\varepsilon}_{i}-\alpha(g_{i}-\rho v_{i})-v_{i}\varepsilon+(\boldsymbol{v\cdot g})v_{i}-v_{j}\pi{ji}</math> | |||
is the heat current | |||
Under dissipationless condition, <math>\frac{\partial S}{\partial t} = 0</math>, and trevious equation can be used to derive Eurel's equation | |||
<math>\frac{\partial \boldsymbol{v}}{\partial t} + \boldsymbol{(v\cdot \nabla)v} = -\frac{1}{\rho}\nabla p</math> | |||
When there is dissipation, | |||
<math>\frac{\partial S}{\partial t} > 0</math>. the dissipative couplings must be between fields and currents with the opposite sign under time reversal. The dissipative current <math>\boldsymbol{Q}</math> will be nonzero, and the stress tensor will acquire a dissipative contribution <math>\sigma^{'}_{ij}</math>, making it | |||
<math>\pi_{ij} = p\delta{ij} + \rho v_{i}v_{j} - sigma^{'}_{ij}</math> | |||
The dissipative Euler equation has the form | |||
<math>T[\frac{\partial \boldsymbol{v}}{\partial t} + \boldsymbol{v\cdot\nabla)v}] = - \nabla \rho + \eta\nabla^{2}\boldsymbol{v} + (\varsigma + \frac{1}{3}\eta)\nabla(\nabla\cdot\boldsymbol{v})</math> | |||
Where <math>\eta</math> is the shear viscocity and <math>\varsigma </math> is the bulk viscocity | |||
====Hydrodynamic Modes==== | |||
There are five conserved hydrodynamic variables, and we expect five low frequency hydrodynamic modes. If the reactive coupling between <math>\rho</math> and <math>\boldsymbol{g}</math> were absent, all of these modes would be diffusive; its presence leads to a pair of longitudinal sound modes. The linearized momentum equation expressed in terms of <math>\boldsymbol{g}</math> rather than <math>\boldsymbol{v}</math> is | |||
<math>\frac{\partial \boldsymbol{g}}{\partial t} + \nabla p - \frac{\eta}{\rho}\nabla^{2}\boldsymbol{g} - \frac{1}{\rho}(\varsigma + \frac{1}{3}\eta)\nabla(\nabla\cdot\boldsymbol{g}) = 0</math> | |||
Because <math>\rho</math> is dynamically coupled only to the longitudinal part of <math>\boldsymbol{g}</math> via the mass conservation equation, it is useful to introduce longitudinal and transverse parts of <math>\boldsymbol{g}</math>: | |||
<math>\boldsymbol{g} = \boldsymbol{g}_{l} + \boldsymbol{g}_{t}</math>,<math>\nabla \times \boldsymbol{g}_{l} = o</math>, <math>\nabla\dot \boldsymbol{g}_{t} = o</math> | |||
<math>\nabla p</math> is longitudinal, so we get | |||
<math>\frac{\partial \boldsymbol{g}_{t}}{\partial t} = \frac{\eta}{\rho}\nabla^{2}\boldsymbol{g}_{t}</math>. | |||
For two transverse components, there are two modes with angular frequency | |||
<math>\omega = -i\frac{\eta}{\rho}q^{2}</math> | |||
The three other modes involve the mass density, the longitudinal momentum and the energy density. | |||
===Hydrodynamics of Nematic Liquid Crystals=== | |||
In the nematic phase, the director <math>\boldsymbol{n}</math>liquid crystal is an elastic variable whose uniform changes do not change the free energy of the system. It is thus a hydrodynamical variable as well. In a theory linearized about a uniform state with <math>\boldsymbol{n} = \boldsymbol{n}_{0} = \boldsymbol{e}_{z}</math>, we may replace <math>\boldsymbol{n}</math> by its deviations <math>\delta n_{x}</math> and <math>\delta n_{y}</math> from <math>\boldsymbol{n}_{0}</math>. The linearized entropy equation for a nematic is, therefore | |||
<math>Tds = d\varepsilon - \alpha d\rho - \boldsymbol{v\cdot{dg}}-h_{ij}d(\nabla_{j}n{i})</math> | |||
where <math>h_{ij} = \frac{\partial \varepsilon}{\partial \nabla_{j}n{i}})_{\rho s g} = K_{jikl}\nabla_{k}n_{l}</math> | |||
Where <math>K_{ijkl}</math> is the Frank elastic constant tensor. | |||
When dissipation is inclued, the entropy production equation becomes | |||
<math>T\frac{\mathrm{d} S}{\mathrm{d} t} = -\int d^{3}x[\boldsymbol{Q}\cdot (\nabla T)/T - \sigma^{'}_{ij}\nabla_{i}v_{j} - X^{'}_{i}\nabla_{j}h_{ij}]</math> | |||
Since the nematic liquid crystal is uniaxial, all dissipative coefficients are tensors. | |||
There are two thermal conductivity coefficients, | |||
<math>k_{ij} = k_{p}n_{i}n_{j} + k_{t}\delta_{ij}^{T}</math> | |||
Five viscosities, | |||
<math>\sigma^{'}_{ij} = 2\nu_{2}A_{ij} + 2(\nu_{3}-\nu_{2})[A_{ik}n_{k}n_{l}+A_{jk}n_{i}n_{k}] - (\nu_{4}-\nu_{2})\delta_{ij}A_{kk} - 2(\nu_{1}+\nu_{2}-2\nu_{3})n_{i}n_{j}n_{k}n_{l}A_{kl} + (\nu_{5}-\nu_{4} +\nu_{2})[\delta_{ij}n_{k}n_{l}A_{kl} + n_{i}n_{j}A{kk}]</math> | |||
Where | |||
<math>A_{ij} = \frac{1}{2}(\nabla_{i}v{j}+\nabla_{j}v_{i})</math> is the strain tensor, and one dissipative coefficient for the director, | |||
<math>X^{'}_{i} = \gamma^{-1}\nabla_{j}h_{ij}</math> | |||
Since there are two additional broken-symmetry variables <math>\delta n_{x}</math> and <math>\delta n_{y}</math>, there are two more modes in a nematic than there are in a isotropic liquid. | |||
===References=== | |||
1. 'Liquid Crystals', Chandrashekhar, Cambridge University Press, 1992. | |||
2. The thesis of | |||
3. G. Friedel Ann. Phyque(Paris)18,273(1922) | |||
4 'Principles of Condensed Matter Physics', Chikin and Lubensky, Cambridge University Press | |||
5. V. Tsvetkov, Macromolecules, 1996, 29 (3), pp 807–808 | |||
Latest revision as of 17:12, 9 December 2010
Introduction
Homogeneous, isotropic liquids have an average structure that is invariant under arbitrary rotations and translations.It has no long range order, and has the highest possible symmetry with maximum possible entropy.The crystalline state has long range translational and rotational order, with the lowest possible symmetry consistent with a regular filling of space. Between these two, there are systems which exhibit short range correlations in some directions and long range in others, and have symmetries intermediate between between those of liquids and crystals.
Among the materials that show intermediate order, the most widely studied are liquid crystals.Liquid crystals are usually made of strongly anisotropic organic molecules, either elongated (calamitic, rod-like molecules) or disk-like (discotic molecules). As a rule, the inner part of mesogenic molecules is rigid (e.g. phenyl groups) and the outer part flexible (aliphatic chains). This double character explains altogether the existence of steric interactions (between rod-like or disk-like cores) yielding orientational order and the fluidity of the mesomorphic phases. Typical examples are cyanobiphenyls and MBBA. These produce thermotropic mesophases,i.e. phases with a single component, whose phase transitions can be induced by a change in temperature.The other broad LC class is constituted by the lyotropic mesophases: they occur when anisotropic amphiphilic molecules (soaps, phospholipids, various types of surfactant molecules and biomolecules) are added to a solvent. Because amphiphiles have two distinct parts, a polar head and a non-polar tail,the building units of lyotropic phases are usually aggregates of many molecules(micelles) rather than single molecules. This microphase separation dominating the lyotropic behavior is partly present also in thermotropic LC, as for example in the smectic phases, where polar and non polar portions of the molecules form distinct alternatinig planes in the system.A typical example of lyotropics is a water solution of SDS, sodium dodecyl sulphate. For concentrations above the critical micellar concentration, cmc, these molecules form aggregates of different shapes, spherical or cylindrical micelles,bilayers, inverse cylinders, and inverse micelles.[1,2.3]
Classification of LC phases
LCs show many possible structures, which can belong to the same compound (polymorphism). There are four basic types of liquid crystalline phases, classified accordingly to the dimensionality of the translational correlations of building units: nematic (no translational correlations), smectic (1D correlation),columnar (2D) and various 3D-correlated structures, such as cubic phases.
Density Correlation and Structure Factor
A lot of information about the bulk structure of LCs can be obtained via scattering of X-rays. let Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\boldsymbol{k}\rangle} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\boldsymbol{k}^{'}\rangle} be the incident and final plane wave state of the scattered particle with respective momenta Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hbar\boldsymbol{k}} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hbar\boldsymbol{k}^{'}} If the scattered particle interacts weakly with the scaterring medium via a sufficiently short-ranged interaction Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U} , then by Fermi's Golden rule, the transition rate between Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\boldsymbol{k}\rangle} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\boldsymbol{k}^{'}\rangle} is proportional to the square of the matrix element,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle M_{\boldsymbol{k},\boldsymbol{k^{'}}} = \langle\boldsymbol{k}|U|\boldsymbol{k^{'}}\rangle = \int d^{d}x e^{-i\boldsymbol{k}.\boldsymbol{x}}U(\boldsymbol{x})e^{i\boldsymbol{k^{'}}.\boldsymbol{x}} }
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U(\boldsymbol{x})} is the scattering potential in the coordinate representation of the scattered particle, and our plane wave states are unnormalized.
In multiparticle systems, the scattering potential is the sum of terms from individual atoms in the material:
\alphaFailed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U(\boldsymbol{x}) = \sum_{\alpha} U_{\alpha}(\boldsymbol{x}-\boldsymbol{x_{'}})} where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \boldsymbol{x_{\alpha}}} is the position of the atom labeled Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha} . the matrix element, therefore, is
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle\boldsymbol{k}|U|\boldsymbol{k^{'}}\rangle = \sum_{\alpha}\int d^{d}x e^{-i\boldsymbol{k}.\boldsymbol{x}}U_{\alpha}(\boldsymbol{x}-\boldsymbol{x_{\alpha}})e^{i\boldsymbol{k^{'}}.\boldsymbol{x}}}
To seperate the potential interaction and the interatomic correlation factors, we shift our centers to each Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_{\alpha}} . Let Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \boldsymbol{R}_{\alpha} = \boldsymbol{x}-\boldsymbol{x_{\alpha}}} .
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle\boldsymbol{k}|U|\boldsymbol{k^{'}}\rangle = \sum_{\alpha}\int d^{d}R_{\alpha} e^{-i\boldsymbol{k}.(\boldsymbol{x}_{\alpha}+\boldsymbol{R}_{\alpha})}U_{\alpha}(\boldsymbol{R}_{\alpha})e^{i\boldsymbol{k^{'}}.(\boldsymbol{x}_{\alpha}+\boldsymbol{R}_{\alpha})} } Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle = \sum_{\alpha}[\int d^{d}R_{\alpha} e^{-i\boldsymbol{q}.\boldsymbol{R}_{\alpha}}U_{\alpha}(\boldsymbol{R}_{\alpha})]e^{-i\boldsymbol{q}.\boldsymbol{x}_{\alpha}}} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle =\sum_{\alpha}U_{\alpha}(\boldsymbol{q})e^{-i\boldsymbol{q}.\boldsymbol{x}_{\alpha}}} Here the scattering wave vector is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \boldsymbol{q} = \boldsymbol{k} - \boldsymbol{k}^{'}} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U_{\alpha}(\boldsymbol{q})} is the atomic form factor, which is nothing but the Fourier transform of the atomic potential. The differential cross-section is proportional to the matrix element squared: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\langle\boldsymbol{k}|U|\boldsymbol{k^{'}}\rangle|^{2} = \sum_{\alpha,\alpha^{'}}U_{\alpha}(\boldsymbol{q})U_{\alpha^{'}}^{*}(\boldsymbol{q})e^{-i\boldsymbol{q}.\boldsymbol{x}_{\alpha}}e^{i\boldsymbol{q}.\boldsymbol{x}_{\alpha^{'}}}}
If the positions of atoms are rigidly fixed,then this expression gives the exact answer. However, in real materials, the particles move around,probing large regions of phase space consistent with statistical mechanics, and we need an ensemble average of the ideal cross-section. Under ergodic hypothesis and assuming the particles are identical,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\mathrm{d}^{2}\sigma }{\mathrm{d} \Omega}\sim |U_{\alpha}(\boldsymbol{q})|^{2}\boldsymbol{I}(\boldsymbol{q})} where the function
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \boldsymbol{I}(\boldsymbol{q}) = \left \langle\sum_{\alpha,\alpha^{'}}e^{-i\boldsymbol{q}.(\boldsymbol{x}_{\alpha}-\boldsymbol{x_{\alpha^{'}}})}\right \rangle} is called the structure function. As intensive version of the structure function is called the structure factor.
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S(\boldsymbol{q}) = \frac{\boldsymbol{I}(\boldsymbol{q})}{N} } or Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S(\boldsymbol{q}) = \frac{\boldsymbol{I}(\boldsymbol{q})}{V}}
Two point density correlation function and its relation with the structure factor
The number density operator is defined as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n(\boldsymbol{x}) = \sum_{\alpha}\delta(\boldsymbol{x}-\boldsymbol{x}_{\alpha})}
The two point density density correlation function is defined as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C_{nn}(\boldsymbol{x}_{1},\boldsymbol{x}_{2}) = \left \langle n(\boldsymbol{x}_{1})n(\boldsymbol{x}_{2})\right \rangle} ) Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle =\left \langle \sum_{\alpha,\alpha^{'}}\delta(\boldsymbol{x}_{1}-\boldsymbol{x}_{\alpha})\delta(\boldsymbol{x}_{2}-\boldsymbol{x}_{\alpha^{'}})\right \rangle}
The structure function is simply a Fourier transform of this function:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \boldsymbol{I}(\boldsymbol{q})= \left \langle n(\boldsymbol{q})n(-\boldsymbol{q})\right \rangle} where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n(\boldsymbol{q}) = \int d^{d}x e^{-i\boldsymbol{k}.\boldsymbol{x}}n(\boldsymbol{x}) = \sum_{\alpha}e^{-i\boldsymbol{k}.\boldsymbol{x}}} is the Fourier transform of the density. In a statistical ensemble, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left \langle n(\boldsymbol{q})\right \rangle = \int d^{d}x e^{-i\boldsymbol{k}.\boldsymbol{x}}\left \langle n(\boldsymbol{x})\right \rangle = \left \langle\sum_{\alpha}e^{-i\boldsymbol{k}.\boldsymbol{x}} \right \rangle} So scattering measures density-density correlation.
Isotropic, nematic and cholesteric phases[4]
In isotropic liquids, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left \langle n(\boldsymbol{x})\right \rangle = \left \langle n \right \rangle} , a constant, so Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left \langle n(\boldsymbol{q})\right \rangle = V \left \langle n \right \rangle \delta _{q,0} } is nonzero only for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \boldsymbol{q} = 0} , and there is a contribution to the structure factor only for forward scattering.
In a regularly periodic crystal, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left \langle n(\boldsymbol{x})\right \rangle = \sum_{\boldsymbol{G}}\left \langle n_{\boldsymbol{G}} \right \rangle e^{-i\boldsymbol{G}.\boldsymbol{x}}} So there is a peak corresponding to each wavevector Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \boldsymbol{G}} in the reciprocal space.
In an Isotropic LCD, the structure factor is isotropic, but shows liquid-like rings at wave numbers corresponding to the two characteristic lengths of the individual molecules-their length l and diameter a.
When the isotropic liquid is cooled, the first phase rhat condenses in the nematic (N)phase in which long molecules align so that they are on an average parallel to a particular direction specified by a unit vector Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \boldsymbol{n}}
called the directorThe positions of the molecular centers of mass remains randomly distributed, like in an isotropic fluid. So the nematic phase breaks rotational invariance but maintains translational invariance. It is easy to visualize that in a statistical ensemble, rotations about Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \boldsymbol{n}}
leaves the phase unchanged, while rotation in a plane perpendicular to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \boldsymbol{n}}
does not. The number density of the nematic phase has two peaks. The structure factor of the nematic phase is axially symmetric in any phase perpendicular to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \boldsymbol{n}}
but has only two-fold symmetry in any plane containing Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \boldsymbol{n}}
. Two possible forms for the X-ray intensity can result. In the first there are diffuse spots at Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \boldsymbol{q}=q_{0}\boldsymbol{n}}
with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle q_{0} = 2\pi/l}
, and in the second there are diffuse rings cetered at the same values of q.
Smectics-A and -C
As temperature is further reduced, molecules begin to segregate into planes giving rise to a smectic-A (Sm-y4) liquid crystal. The usual picture of this smectic phase is one with molecules situated in well-defined layers with a spacing that is essentially the rod length. There is liquid-like motion of the rods in each layer and no correlation of the positions of the molecules from one layer to the next. In smectic-,4 liquid crystals, molecules are aligned perpendicular to the layers. The introduction of the layering indicates the presence of a mass density wave perpendicular to the layers. There is, therefore, positional correlation in the system which can be described as a sinusoidal modulation of the average molecular number-density,
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left \langle n(\boldsymbol{x})\right \rangle = n_{0} + 2n_{q_{0}}\cos({q_0}z)}
where the z-axis is along the layer normals and parallel to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \boldsymbol{n}} . From this, we get
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S(\boldsymbol{q}) = |\left \langle n_{q_{0}}\right \rangle|^{2}(2\pi)^{3}[\delta(\boldsymbol{q}_{z} - q_{0}\boldsymbol{e}_{z}) + \delta(\boldsymbol{q}_{z}+q_{0}\boldsymbol{e}_{z})]}
In some systems, molecules align along an axis tilted relative to the smectic planes. This is the smectic-C phase. It has a lower symmetry than the smectic-,4 phase because the tilted molecules pick out a special direction in the smectic plane, i.e., their projections in the xy-plane align,like the molecules in a nematic, along a common direction denoted by a unit vector Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \boldsymbol{e}} , called the e-director. There are in fact transitions from the smectic-A to the smectic-C phase in which the tilt angle grows continuously from zero. The structure factor of the nematic phase just above a smectic-C phase has diffuse rings rather than diffuse spots.
Hexatic Phases
When smectic-A phases are cooled, they condense into what was historically called a smectic-B phase. It is now known that a smectic-B phase can be a crystalline-B phase with a three-dimensional crystal structure and Bragg scattering at points in a three-dimensional reciprocal lattice. In some cases, however, the smectic-B phase is not a true crystal. It has hexagonal orientational order manifested by the development of a six-fold modulation in the intensity of the diffuse ring at q = 2n/a in the X-ray scattering intensity of the smectic-,4 phase. Whereas the smectic-,4 phase is invariant with respect to arbitrary rotations about Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \boldsymbol{n}} ,this hexatic-B phase is invariant only with respect to rotations of 2n/6 about Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \boldsymbol{n}} .
Discotic and Columnar Phases
The nematic and smectic phases just discussed are generally found in materials consisting of rod-like molecules. Plate-like rather than rod-like molecules can form discotic nematic phases, in which the plate normals are aligned, as well as phases with crystalline order in two dimensions and liquid-like order in the third direction. The latter are called columnar. The plate-like molecules segregate into columns with the plate normals either parallel to or tilted at an angle to the columnar axes. There is no long-range positional order within a column. The columns themselves form any of the two-dimensional crystals.
The First Order Nematic-to-Isotropic Transition
Suppose that the liquid crystal is composed of rod-like molecules in which (i) the distribution function is cylindrically symmetric about the axis of preferred orientation n and (ii) the directions Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \boldsymbol{n}} and are fully equivalent, i.e., the preferred axis is non-polar. Subject to these two symmetry properties, and assuming the rods to be cylindrically symmetric, the simplest way of defining the degree of alignment is by the parameter s, first introduced by Tsvetkov[5]
where is the angle which the long molecular axis makes with . For perfectly parallel alignment , while for random orientations
The next task is to create an order parameter. Although it is tempting to associate the order parameter with an unit vector along the long axis direction of molecule located at .However, we note that a rotation by leaves the phase unchanged, and so the order prameter must be an even function of . So we look for the next option, which is a symmetric traceless tensor, which, as needed, yields zero when averaged over all directions
Where the unit vector n is the Frank director, and where is the angle between the molecular axis and the director n.
Now the Landau free energy must be invariant under all rotations. Since Q is a tensor, the only way, to the fourth order, is
Since Q is a traceless tensor, the first term is zero, so
We choose
w and u are temperature independent. Note the presence of the cubic term, which is a consequence of the quadrupolar symmetry of the molecules and the resultant tensor property of the order parameter. is sketched as a function of for various values of T in figure ??????.Note that the cubic term leads to an asymmetry in as a function of S and the emergence of a secondary minimum at finite S. The value of at this minimum is greater than zero at high temperature but becomes equal to zero at a critical temperature Tc that is greater than the temperature T* at which the extremum at the origin develops negative curvature. Since / is less than zero at the secondary minimum for all T < Tc, there is a phase transition with a discontinuous change in S at Tc, i.e. there is a first-order transition at Tc. T* is the limit of metastability of the isotropic phase since, for T* < T < Tc, the origin is still a local minimum even though it is not a global minimum. The limit of metastability of the nematic phase occurs at the temperature T" at which the secondary minimum disappears on heating. The first-order transition temperature Tc and the value Sc of S at Tc are calculated by requiring that / be an extremum with respect to S in equilibrium and that the free energies of the disordered and ordered phases be equal at the transition. The latter condition implies that the isotropic and nematic phases can coexist at the transition temperature. If other variables, such as pressure or density, were included in our treatment, the two phases would coexist along a line rather than at a single point. The equations determining Tc and Sc are, therefore,
Thus, ,
The transition being first order, there is an associated latent heat.heat. The entropy per unit volume of the disordered phase is zero in mean-field theory, whereas that of the nematic phase is negative. This result can be obtained from the freeenergy of the nematic phase, which to lowest order in is
The entropy density relative to the isotropic phase is therefore
The latent heat absorbed in going from the nematic to the isotropic phase is
Hydrodynamics of Liquid Crystals
Basic introduction
Thermodynamic equilibrium is produced and maintained by collisions between particles or elementary excitations that occur at a characteristic time interval math>\tau</math>. In classical fluids, is of order to seconds. In low-temperature solids or in quantum liquids, can be quite large, diverging as some inverse power of the temperature . The mean distance A between collisions (mean free path) of particles or excitations is a characteristic velocity times . In fluids, is determined by the kinetic energy, , where is a mass. In solids, is typically a sound velocity. Imagine now a disturbance from the ideal equilibrium state that varies periodically in time and space with frequency and wave number . If and , the disturbance varies slowly on time and length scales set by and , and there will be many equilibrating collisions in each of its temporal and spatial cycles. Thus, each point in space is close to thermodynamic equilibrium at each instant of time, and one would expect to be able to treat such disturbances as perturbations from thermodynamic equilibrium even though they vary in time.Most disturbances in many body systems have characteristic frequencies that are of order . If excited, they decay rapidly to equilibrium. There are, however, certain classes of variables that are guaranteed to have slow temporal variations at long wavelengths. These are
A) densities of conserved variables, and B) broken-symmetry elastic variables.
A conserved density such as the number density n obeys a conservation law of the form
where is the particle current.When Fourier transformed, such equations imply frequencies that go to zero with wave number . Out of our hydrodynamical analysis, we shall derive some important concepts, which are:
• Long-wavelength, low-frequency excitations are associated with conservation laws and broken symmetry.
• There is exactly one mode associated with each conservation law and each broken symmetry.
• Currents of hydrodynamical variables contain reactive and dissipative parts.The reactive parts of currents couple variables of opposite sign under time reversal and lead to propagating modes.
• In the absence of reactive couplings, the hydrodynamical modes are diffusive.
• Diffusion constants are the ratio of a transport coefficient to a susceptibility.
• The velocities of propagating modes are square roots of the ratio of a reactive transport coefficient to a susceptibility.
Hydrodynamics of Isotropic fluids
Conservation laws
Due to the possibility of mass motion and possibility of relative motion of different parts of the fluid, there are conservation laws for mass and momentum in addition to that of energy, leading to five conserved hydrodynamical variables (2 for energy and mass, one each for each component of momentum) and five hydrodynamic modes. The respective density operators are
where is the two-body interaction potential.These densities obey local conservation laws
where is the energy current and is the momentum current tensor.Note that the conserved momentum density is itself a current for another conserved density, the mass density.The conservation laws apply to averaged densities , and as well as to other microscopic operators. Angular momentum is conserved but is not independent of
Thermodynamics
The total Hamiltonian of this system is
, Where is the total momentum operator and
the average of is the internal energy . The canonical partition function for a fluid with N particles in a volume V is then
the thermodynamic potential,
satisfies
We also get the entropy equation
Constitutive relations from the entropy equation
Using the entropy relation and the conservation laws, we get,
We can write this as
![{\displaystyle T[{\frac {\partial s}{\partial t}}+\nabla \cdot {({\boldsymbol {v}}s+{\frac {1}{T}}{\boldsymbol {Q}})}]=-{\boldsymbol {Q}}\cdot {(\nabla {T}/T)}-({\boldsymbol {g}}-\rho {\boldsymbol {v}})\cdot \nabla \alpha -[\pi _{ji}-p\delta _{ij}-v_{i}g_{j}]\nabla _{i}v_{j}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0069603de698a0f3063a6b4753d235a2ef237e0f)
Where is the pressure derived from the thermodynamic potential and
is the heat current
Under dissipationless condition, , and trevious equation can be used to derive Eurel's equation
When there is dissipation,
. the dissipative couplings must be between fields and currents with the opposite sign under time reversal. The dissipative current will be nonzero, and the stress tensor will acquire a dissipative contribution , making it
The dissipative Euler equation has the form
![{\displaystyle T[{\frac {\partial {\boldsymbol {v}}}{\partial t}}+{\boldsymbol {v\cdot \nabla )v}}]=-\nabla \rho +\eta \nabla ^{2}{\boldsymbol {v}}+(\varsigma +{\frac {1}{3}}\eta )\nabla (\nabla \cdot {\boldsymbol {v}})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0281814bac1043d06b2b01b7e471181508517ad7)
Where is the shear viscocity and is the bulk viscocity
Hydrodynamic Modes
There are five conserved hydrodynamic variables, and we expect five low frequency hydrodynamic modes. If the reactive coupling between and were absent, all of these modes would be diffusive; its presence leads to a pair of longitudinal sound modes. The linearized momentum equation expressed in terms of rather than is
Because is dynamically coupled only to the longitudinal part of via the mass conservation equation, it is useful to introduce longitudinal and transverse parts of :
,,
is longitudinal, so we get
.
For two transverse components, there are two modes with angular frequency
The three other modes involve the mass density, the longitudinal momentum and the energy density.
Hydrodynamics of Nematic Liquid Crystals
In the nematic phase, the director liquid crystal is an elastic variable whose uniform changes do not change the free energy of the system. It is thus a hydrodynamical variable as well. In a theory linearized about a uniform state with , we may replace by its deviations and from . The linearized entropy equation for a nematic is, therefore
where
Where is the Frank elastic constant tensor.
When dissipation is inclued, the entropy production equation becomes
![{\displaystyle T{\frac {\mathrm {d} S}{\mathrm {d} t}}=-\int d^{3}x[{\boldsymbol {Q}}\cdot (\nabla T)/T-\sigma _{ij}^{'}\nabla _{i}v_{j}-X_{i}^{'}\nabla _{j}h_{ij}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3fbb8d42db19061ead850b2f6f2da536d8ad912f)
Since the nematic liquid crystal is uniaxial, all dissipative coefficients are tensors. There are two thermal conductivity coefficients,
Five viscosities,
![{\displaystyle \sigma _{ij}^{'}=2\nu _{2}A_{ij}+2(\nu _{3}-\nu _{2})[A_{ik}n_{k}n_{l}+A_{jk}n_{i}n_{k}]-(\nu _{4}-\nu _{2})\delta _{ij}A_{kk}-2(\nu _{1}+\nu _{2}-2\nu _{3})n_{i}n_{j}n_{k}n_{l}A_{kl}+(\nu _{5}-\nu _{4}+\nu _{2})[\delta _{ij}n_{k}n_{l}A_{kl}+n_{i}n_{j}A{kk}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/46a1714497414a1931262b70a4cd5f367ab13637)
Where
is the strain tensor, and one dissipative coefficient for the director,
Since there are two additional broken-symmetry variables and , there are two more modes in a nematic than there are in a isotropic liquid.
References
1. 'Liquid Crystals', Chandrashekhar, Cambridge University Press, 1992.
2. The thesis of
3. G. Friedel Ann. Phyque(Paris)18,273(1922)
4 'Principles of Condensed Matter Physics', Chikin and Lubensky, Cambridge University Press
5. V. Tsvetkov, Macromolecules, 1996, 29 (3), pp 807–808