Phy5670/HubbardModel 2: Difference between revisions
| (71 intermediate revisions by the same user not shown) | |||
| Line 7: | Line 7: | ||
== The Symmetries of Hubbard model == | == The Symmetries of Hubbard model == | ||
=== Global <math>U(1)</math> Symmetry (Charge | === Global <math>U(1)</math> Symmetry (Charge) === | ||
We are free to change he phase of the one-particle wavefunction | |||
:<math>a'_{\sigma}(\vec{r}) = e^{i\theta}a_{\sigma}(\vec{r})</math> | |||
Here, <math>e^{i\theta}</math> is an element of the group <math>U(1)</math>, and the group elements satisfy | |||
:<math>e^{i\theta}e^{i\theta'} = e^{i\left(\theta + \theta'\right)}</math> | |||
The hamiltonian is invariant under this <math>U(1)</math> transformation. This is nothing but charge conservation. For example, if we had terms which would not conserve charge, like | |||
:<math>a_{\sigma}^{\dagger}(\vec{r})a_{\sigma}^{\dagger}(\vec{r'}) \rightarrow e^{i2\theta}a_{\sigma}^{\dagger}(\vec{r})a_{\sigma}^{\dagger}(\vec{r'})</math> | |||
we would not have this invariance.<br> | |||
It is convenient to define the spin operator <math>\vec{S}_{\mathbf{i}}</math> as | It is convenient to define the spin operator <math>\vec{S}_{\mathbf{i}}</math> as | ||
:<math>\vec{S}_{\ | |||
:<math>\vec{S}(\vec{r}) = \frac{\hbar}{2}a_{\sigma}^{\dagger}(\vec{r})\vec{\tau}_{\sigma\sigma'}a_{\sigma}(\vec{r})</math> | |||
where <math>\vec{\tau}</math> are the (three) Pauli matrices | |||
:<math>\tau_{1} = \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix}, \tau_{2} = \begin{pmatrix} 0 & -i \\ i & 0 \end{pmatrix}, \tau_{3} = \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix}.</math> | |||
Suppose now that we couple this system to the electromagnetic field <math>\left(A_{0},\vec{A}\right)</math>. we expect three effects. | |||
:1) A Zeeman coupling given by | |||
::<math>H_{Zeeman} = g\sum_{\vec{r}}\vec{S}(\vec{r})\cdot\vec{B}(\vec{r})</math> | |||
which couples the spin <math>\vec{S}(\vec{r})</math> with the local magnetic field <math>\vec{B}(\vec{r})</math> so as to align it along the <math>\vec{B}(\vec{r})</math> direction. | |||
:2) An orbital coupling for electrons in a crystal with one-particle hamiltonian | |||
::<math>H(\vec{p}) = \frac{1}{2m_{e}}\left(\vec{p}-\frac{e}{c}\vec{A}\right)^{2}</math> + periodic potential. | |||
In the tight-binding approximation, we must therefore modify the kinetic energy term according to | |||
::<math>H_{0} \equiv -t\sum_{\left(\vec{r},\vec{r'}\right) \atop \sigma = \uparrow,\downarrow}\left(a_{\sigma}^{\dagger}(\vec{r})a_{\sigma}(\vec{r'}) + h.c.\right) \rightarrow -t\sum_{\left(\vec{r},\vec{r'}\right) \atop \sigma = \uparrow,\downarrow}\left(a_{\sigma}^{\dagger}(\vec{r})e^{\frac{ie}{\hbar c}\int_{\vec{r}}^{\vec{r'}}d\vec{x}\vec{A}(\vec{x})}a_{\sigma}(\vec{r'}) + a_{\sigma}^{\dagger}(\vec{r'})e^{-\frac{ie}{\hbar c}\int_{\vec{r}}^{\vec{r'}}d\vec{x}\vec{A}(\vec{x})}a_{\sigma}(\vec{r})\right)</math> | |||
It is easy to be verified that under the gauge transformation | |||
<math>\vec{A'} = \vec{A} + \vec{\Delta}\Lambda</math> | |||
the local change of phase is given by <math>\theta(\vec{r}) \equiv -\frac{e}{\hbar c}\Lambda(\vec{r})</math> | |||
:3)An electrostatic coupling | |||
::<math>H_{electrostatic} = \sum_{\vec{r},\sigma}eA_{0}(\vec{r})a_{\sigma}^{\dagger}(\vec{r})a_{\sigma}(\vec{r})</math><br> | |||
which couples the particle density to <math>A_{0}(\vec{r})</math> | |||
=== Global spin <math>SU(2)</math> symmetry === | |||
Suppose we rotate the local spin basis (i.e. the quantization axis) | |||
:<math>a_{\sigma}'(\vec{r}) = U_{\sigma\sigma'}a_{\sigma'}(\vec{r})</math> | |||
where <math>U</math> is an <math>SU(2)</math> matrix. Under such a unitary transformation, the spin operator <math>\vec{S}</math> transforms as follows | |||
:<math>\vec{S'}^{\alpha}(\vec{r}) = R^{\alpha\beta}\vec{S}^{\beta}(\vec{r}) = \frac{\hbar}{2}a^{\dagger}(\vec{r})(U^{-1}\vec{\tau}^{\alpha}U)a(\vec{r})</math> | |||
where <math>R^{\alpha\beta}</math> is a rotation matrix induced by the <math>SU(2)</math> transformation of the fermions:<br> | |||
:<math>R^{\alpha\beta}\vec{\tau}^{\beta} = U^{-1}\vec{\tau}^{\alpha}U</math> | |||
In other words, we have a rotation of the quantization axis. | |||
The axis of quantization can be chosen arbitrarily. Thus, the Hubbard model Hamiltonian should not change its form under a rotation of the spin quantization axis. This is not apparent in the standard form of the interaction term. | |||
:<math>H_{int} = U\sum_{\vec{r}}n_{\uparrow}(\vec{r})n_{\downarrow}(\vec{r})</math>. | |||
But we can write this in a somewhat different form in which the <math>SU(2)</math> symmetry become explicit. Consider the operator | |||
:<math>\vec{S}^{2}(\vec{r}) = \frac{\hbar^{2}}{4}a_{\sigma}^{\dagger}\tau_{\sigma\sigma'}^{i}a_{\sigma'}a_{\rho}^{\dagger}\tau_{\rho\rho'}^{i}a_{\rho'}</math> | |||
By the field identity | |||
:<math>\sum_{i = 1,2,3}\tau_{\sigma\sigma'}^{i}\tau_{\rho\rho'}^{i} = 2\delta_{\sigma\rho}\delta_{\sigma'\rho'} - \delta_{\sigma\sigma'}\delta_{\rho\rho'}</math> | |||
we get | |||
:<math>\sum_{\vec{r}}\vec{S}^{2}(\vec{r}) = \sum_{\vec{r}}\left(\frac{1}{4}n(\vec{r})-\frac{3}{2}n_{\uparrow}(\vec{r})n_{\downarrow}(\vec{r})\right)</math> | |||
Thus we can write | |||
:<math>H_{int} = U\sum_{\vec{r}}n_{\uparrow}(\vec{r})n_{\downarrow}(\vec{r}) = -\frac{2U}{3}\vec{S}^{2}(\vec{r}) + \frac{N_{e}U}{6}</math>. | |||
where <math>N_{e}</math> is the total number of electrons. The Hamiltonian now takes the form | |||
:<math>H = -t\sum_{\left(\vec{r},\vec{r'}\right) \atop \sigma = \uparrow,\downarrow}\left(a_{\sigma}^{\dagger}(\vec{r})a_{\sigma}(\vec{r'}) + h.c.\right) - \sum_{\vec{r}}\frac{2U}{3}\vec{S}^{2}(\vec{r}) + \frac{N_{e}U}{6}</math> | |||
which is manifestly <math>SU(2)</math> invariant. | |||
For <math>U > 0</math>, the interaction energy is lowered if the total spin at each site is maximized. Thus, one would expect some sort of magnetic ground state, at least each site has one particle (on the average). This state requires that the system somehow should pick a global quantization axis. In other words, the global <math>SU(2)</math> spin symmetry may be spontaneously broken. | |||
=== <math>SO_{4}</math> symmetry === | |||
For a simple Hubbard model, using a particle-particle paring operator <math>\eta</math> and a particle-hole pairing operator <math>\zeta</math>, it is shown that one can write down two commuting sets of angular momenta operators <math>\mathbf{J}</math> and <math>\mathbf{J}'</math>, both of which commute with the Hamiltonian. These considerations allow the introduction of quantum numbers <math>j</math> and <math>j'</math>, and lead to the fact that the system has <math>SO_{4} = \left(SU(2) \times SU(2)\right) / Z_{2}</math> symmetry. <math>j</math> is related to the existence of superconductivity for a state and <math>j'</math> to its magnetic properties. | |||
we may want to split the Hamiltonian into two parts | |||
:<math>H = V + T</math>, | |||
under Fourier transformation <math>a_{\sigma}(\mathbf{r}) = \frac{1}{(2\pi)^{3/2}}\sum_{\mathbf{k}}e^{i\mathbf{k}\mathbf{r}}a_{\mathbf{k},\sigma}</math>, | |||
:<math>T = -2t\sum_{\mathbf{k}}\left(\cos k_{x} + \cos k_{y} + \cos k_{z}\right)\left(a_{\mathbf{k}}^{\dagger}a_{\mathbf{k}} + b_{\mathbf{k}}^{\dagger}b_{\mathbf{k}}\right)</math>, | |||
:<math>V = 2W\sum_{\mathbf{r}}\left(a_{\mathbf{r}}^{\dagger}a_{\mathbf{r}} - \frac{1}{2}\right)\left(b_{\mathbf{r}}^{\dagger}b_{\mathbf{r}} - \frac{1}{2}\right)</math>, | |||
:<math>\mathbf{P} = \sum\left(\mathbf{k} - \frac{1}{2}\mathbf{\pi}\right)\left(a_{\mathbf{k}}^{\dagger}a_{\mathbf{k}} + b_{\mathbf{k}}^{\dagger}b_{\mathbf{k}}\right)(\mathbf{mod.}2\mathbf{\pi})</math>. | |||
1) Defining | |||
:<math>\eta^{\dagger} = J_{x} + iJ_{y}, \quad \eta = J_{x} - iJ_{y}, \quad J_{z} = \frac{1}{2}\sum\left(a_{\mathbf{k}}^{\dagger}a_{\mathbf{k}} + b_{\mathbf{k}}^{\dagger}b_{\mathbf{k}}\right) - \frac{1}{2}M</math>, | |||
It is easy to verify that <math>\eta^{\dagger}\eta - \eta\eta^{\dagger} = \sum\left(a_{\mathbf{k}}^{\dagger}a_{\mathbf{k}} + b_{\mathbf{k}}^{\dagger}b_{\mathbf{k}}\right) - M</math>, where <math>M = L^{3}</math>. One also finds that <math>J_{x}</math>, <math>J_{y}</math>, <math>J_{z}</math> commute with each other just like the components of an angular momentum. Hence the eigenvalue of <math>\mathbf{J}^{2}</math> is <math>j(j+1)</math> where <math>2j = integer \geq 0</math>. Fuether more | |||
:<math>[T,\mathbf{J}]_{-} = [V,\mathbf{J}]_{-} = [H,\mathbf{J}]_{-} = [\mathbf{P},\mathbf{J}]_{-} = 0</math>. | |||
2) We now define a particle-hole pairing operator | |||
:<math>\zeta = \sum a_{\mathbf{k}}b_{\mathbf{k}}^{\dagger} = a_{\mathbf{r}}b_{\mathbf{r}}^{\dagger}</math>, | |||
Then | |||
:<math>\zeta^{\dagger}\zeta - \zeta\zeta^{\dagger} = -\sum a^{\dagger}a + \sum b^{\dagger}b</math>. | |||
Similarly, by defining | |||
:<math>\zeta^{\dagger} = J'_{x} + iJ'_{y}, \quad \zeta = J'_{x} - iJ'_{y}, \quad J'_{z} = \frac{1}{2}\sum a^{\dagger}a - \frac{1}{2}\sum b^{\dagger}b</math>, | |||
one finds that <math>J'_{x}</math>, <math>J'_{y}</math>, <math>J'_{z}</math> commute with each other just like the components of an angular momentum. Hence the eigenvalue of <math>\mathbf{J}'^{2}</math> is <math>j'(j'+1)</math> where <math>2j' = integer \geq 0</math>. Furthermore all 3 components of <math>\mathbf{J}</math> commute with all 3 components of <math>\mathbf{J}'</math>, and | |||
:<math>[T,\mathbf{J}']_{-} = [V,\mathbf{J}']_{-} = [H,\mathbf{J}']_{-} = [\mathbf{P},\mathbf{J}']_{-} = 0</math>. | |||
<math>\zeta</math> is the usual spin lowering operator and <math>\mathbf{J}'</math> is the usual "spin" operator. | |||
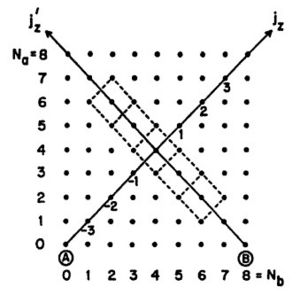
3) We diagonalize <math>\mathbf{J}^{2}</math>, <math>\mathbf{J}'^{2}</math>, <math>J_{z}</math>, <math>J'_{z}</math>, <math>H</math> and <math>\mathbf{P}</math> simultaneously with the definition in 1) and 2). We can find many eigenstates of H, which can be sort out into multiplets <math>\{j,j'\}</math>, each comprising of <math>(2j+1)(2j'+1)</math> states, as illustrated in the figure, where <math>N_{a}</math> and <math>N_{b}</math> are eigenvalues of <math>\sum a^{\dagger}a</math> and <math>\sum b^{\dagger}b</math>,<br> | |||
[[Image:HM_fig1.jpg|thumb|300px|right|Fig.1]] | |||
<br> | |||
Figure. 1 is the <math>(N_{a}, N_{b})</math> diagram for <math>M = 8</math>. The relationship between <math>(j_{z}, j'_{z})</math> with <math>(N_{a}, N_{b})</math> is given by | |||
:<math>j_{z} = \frac{1}{2}\left(N_{a} + N_{b} - M\right), \quad j'_{z} = \frac{1}{2}\left(N_{a} - N_{b}\right)</math>. | |||
Each multiplet <math>\{j, j'\}</math> is represented by a rectangular set of states centered at <math>j_{z} = j'_{z} = 0</math> in this diagram. The number of states in the multiplet is <math>(2j + 1)(2j' + 1)</math>. Illustrated is the multplet <math>\{\frac{1}{2}, \frac{5}{2}\}</math>. All states of a multiplet share the same eigenvalue of <math>H</math> and <math>\mathbf{P}</math>. The lowest corner in the multiplet is where <math>j_{z} = -j, j'_{z} = -j'</math>. One can generate all states of a multiplet by starting from its lowest corner and repeatly operate on it with <math>\eta^{\dagger} = J_{x} + iJ_{y}</math> (which increases <math>j_{z}</math>) and with <math>\zeta^{\dagger} = J'_{x} + iJ'_{y}</math> (which increases <math>j'_{z}</math>). Obviously <math>j + j' = </math>integer. Notice that for fixed <math>j</math> and <math>j'</math>, there are in general a large number of multiplets <math>\{j, j'\}</math>, except for <math>\{\frac{M}{2}, 0\}</math> and <math>\{0, \frac{M}{2}\}</math>, each of which occurs only once. For the former, the lowest corner is the point <math>A</math> where <math>N_{a} = N_{b} = 0</math> which is a single state. For the later, the lowest corner is B where <math>N_{a} = 0</math>, <math>N_{b} = M</math> which is also a single state. | |||
== References == | |||
[1] "η pairing and off-diagonal long-range order in a Hubbard model" C.N.Yang, Phys. Rev. Lett. 63, 2144–2147 (1989) [http://prl.aps.org/abstract/PRL/v63/i19/p2144_1] | |||
[2] "<math>SO_{4}</math> Symmetry in a Hubbard Model" C.N.Yang, Mod. Phys. Lett. B4 (1990) 759-766 | |||
[3] "New Approach to the Theory of Superexchange Interactions" P. W. Anderson, Phys. Rev. 115, 2 (1959) [http://prola.aps.org/abstract/PR/v115/i1/p2_1] | |||
[4] "Theory of Ferromagnetism and the Ordering of Electronic Energy Levels" E. Lieb and D.C. Mattis, Phys. Rev. 125, 164 (1962) [http://prola.aps.org/abstract/PR/v125/i1/p164_1] | |||
[5] "Field Theories of Condensed Matter Systems" E. Fradkin, Addson-Wesley Redwood City (1991) | |||
Latest revision as of 23:49, 9 December 2010
Introduction
The model referred to as the Hubbard model appeared in the literature for the first time in 1963, in two subsequent independent papers -- the first by Gutzwiller, and the second by Hubbard -- as an attempt to describe in a simplified way the effect of correlations for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle d}
-electrons in a transition metals, In deed in the latter case the feature that electrons form a (narrow) delocalized Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle d}
-band is in competition with the quasi-atomic behavior originated from correlations, which would make plausible an atomic description of the problem. The model hamiltonian Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H}
consists of two contributions,
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H = \sum_{\mathbf{i},\mathbf{j}}\sum_{\sigma}t_{\mathbf{i},\mathbf{j}}\left(a_{\mathbf{i},\sigma}^{\dagger}a_{\mathbf{j},\sigma} + h.c.\right) + U\sum_{\mathbf{i}}n_{\mathbf{i},\uparrow}n_{\mathbf{i},\downarrow}} , (1.1.1)
a kinetic term describing the motion of electrons between neighboring sites (the hopping integral Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t_{\mathbf{i},\mathbf{j}}} is usually restricted to nearest-neighbors, and is assumed translationally invariant, namely Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t_{\mathbf{i},\mathbf{j}} = -t, t > 0} ), and an on-site term, which approximates the interactions among electrons, whose strength is given by the parameter Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U} . Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U > 0} corresponds to repulsive Coulomb interaction, whereas Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U < 0} could eventually describe an effective attractive interaction mediated by the ions. Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{i},\mathbf{j}} label the sites of a Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D} -dimensional lattice Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{\Lambda}} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma = \uparrow,\downarrow} denotes the spin, and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_{\mathbf{i},\sigma}^{\dagger},a_{\mathbf{j},\sigma}} are the electrons creation and annihilation operators, with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n_{\mathbf{i},\sigma} = a_{\mathbf{i},\sigma}^{\dagger}a_{\mathbf{i},\sigma}} . Hamiltonian (1.1.1) is expected to be capable of describing the main collective features of above materials, namely itinerant magnetism and metal-insulator (Mott) transition. Indeed, for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U = 0} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H} reduces to a system of non-interacting moving electrons, while for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t = 0} (atomic limit) the electrons are fully localized, and at half-filling the ground state contains exactly one electron per site, i.e. the system is insulating. The later feature still holds for finite Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U = \infty} , and the corresponding system has been shown to be an anti-ferromagnetic insulator. A first question is then for which correlation strength one has the Mott transition, and under which conditions the system exhibits (anti-) ferromagnetic long-range order. Besides, one would like to know how these features depend on temperature, as well as on the filling band. The latter can be controlled, as usual, through the chemical potential Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu} , by adding to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H} a term Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -\mu\sum_{\mathbf{i},\sigma}n_{\mathbf{i},\sigma}} , and fixing then Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu} so that the expectation value of the electron number operator per site is equal to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2\delta} . At half-filling and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T = 0} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu = U/2} . Notice that the case Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta > \frac{1}{2}} can be discussed similarly to the case Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta < \frac{1}{2}} by considering holes instead of electrons, and changing the sign of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t} . A considerable amount of work has been devoted to the solution of the Hubbard model since its introduction in physics. Nevertheless, exact results are still very rare, and there validity is mainly confined to the one-dimensional case, in which the metal-insulator transition is absent at any Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T \neq 0} , according to the Mermin-Wagner theorem on the absence of long-range order in one- (and two-) dimensional systems. Even at Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T = 0} the exact solution exhibits no metal-insulator transition for any Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U > 0} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta} , and the magnetic properties of the model turn out to be peculiar of the dimension, in particular that of having always a total average spin equal to zero. Many diverse approaches have been proposed in order to gain information about the behavior of such an oversimplified system. See section 1.2 for details.
The Symmetries of Hubbard model
Global Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U(1)} Symmetry (Charge)
We are free to change he phase of the one-particle wavefunction
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a'_{\sigma}(\vec{r}) = e^{i\theta}a_{\sigma}(\vec{r})}
Here, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e^{i\theta}} is an element of the group Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U(1)} , and the group elements satisfy
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e^{i\theta}e^{i\theta'} = e^{i\left(\theta + \theta'\right)}}
The hamiltonian is invariant under this Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U(1)} transformation. This is nothing but charge conservation. For example, if we had terms which would not conserve charge, like
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_{\sigma}^{\dagger}(\vec{r})a_{\sigma}^{\dagger}(\vec{r'}) \rightarrow e^{i2\theta}a_{\sigma}^{\dagger}(\vec{r})a_{\sigma}^{\dagger}(\vec{r'})}
we would not have this invariance.
It is convenient to define the spin operator Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{S}_{\mathbf{i}}} as
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{S}(\vec{r}) = \frac{\hbar}{2}a_{\sigma}^{\dagger}(\vec{r})\vec{\tau}_{\sigma\sigma'}a_{\sigma}(\vec{r})}
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{\tau}} are the (three) Pauli matrices
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tau_{1} = \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix}, \tau_{2} = \begin{pmatrix} 0 & -i \\ i & 0 \end{pmatrix}, \tau_{3} = \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix}.}
Suppose now that we couple this system to the electromagnetic field Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(A_{0},\vec{A}\right)} . we expect three effects.
- 1) A Zeeman coupling given by
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H_{Zeeman} = g\sum_{\vec{r}}\vec{S}(\vec{r})\cdot\vec{B}(\vec{r})}
which couples the spin Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{S}(\vec{r})} with the local magnetic field Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{B}(\vec{r})} so as to align it along the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{B}(\vec{r})} direction.
- 2) An orbital coupling for electrons in a crystal with one-particle hamiltonian
- + periodic potential.
In the tight-binding approximation, we must therefore modify the kinetic energy term according to
It is easy to be verified that under the gauge transformation
the local change of phase is given by
- 3)An electrostatic coupling
which couples the particle density to
Global spin symmetry
Suppose we rotate the local spin basis (i.e. the quantization axis)
where is an matrix. Under such a unitary transformation, the spin operator transforms as follows
where is a rotation matrix induced by the transformation of the fermions:
In other words, we have a rotation of the quantization axis.
The axis of quantization can be chosen arbitrarily. Thus, the Hubbard model Hamiltonian should not change its form under a rotation of the spin quantization axis. This is not apparent in the standard form of the interaction term.
- .
But we can write this in a somewhat different form in which the symmetry become explicit. Consider the operator
By the field identity
we get
Thus we can write
- .
where is the total number of electrons. The Hamiltonian now takes the form
which is manifestly invariant. For , the interaction energy is lowered if the total spin at each site is maximized. Thus, one would expect some sort of magnetic ground state, at least each site has one particle (on the average). This state requires that the system somehow should pick a global quantization axis. In other words, the global spin symmetry may be spontaneously broken.
symmetry
For a simple Hubbard model, using a particle-particle paring operator and a particle-hole pairing operator , it is shown that one can write down two commuting sets of angular momenta operators and , both of which commute with the Hamiltonian. These considerations allow the introduction of quantum numbers and , and lead to the fact that the system has symmetry. is related to the existence of superconductivity for a state and to its magnetic properties.
we may want to split the Hamiltonian into two parts
- ,
under Fourier transformation ,
- ,
- ,
- .
1) Defining
- ,
It is easy to verify that , where . One also finds that , , commute with each other just like the components of an angular momentum. Hence the eigenvalue of is where . Fuether more
- .
![{\displaystyle [T,\mathbf {J} ]_{-}=[V,\mathbf {J} ]_{-}=[H,\mathbf {J} ]_{-}=[\mathbf {P} ,\mathbf {J} ]_{-}=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b250c12b685f43c0792c7fc0577f106e28f063b2)
2) We now define a particle-hole pairing operator
- ,
Then
- .
Similarly, by defining
- ,
one finds that , , commute with each other just like the components of an angular momentum. Hence the eigenvalue of is where . Furthermore all 3 components of commute with all 3 components of , and
- .
![{\displaystyle [T,\mathbf {J} ']_{-}=[V,\mathbf {J} ']_{-}=[H,\mathbf {J} ']_{-}=[\mathbf {P} ,\mathbf {J} ']_{-}=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/32aff094b4348b8bd25f72b1051d2d19495f9134)
is the usual spin lowering operator and is the usual "spin" operator.
3) We diagonalize , , , , and simultaneously with the definition in 1) and 2). We can find many eigenstates of H, which can be sort out into multiplets , each comprising of states, as illustrated in the figure, where and are eigenvalues of and ,
Figure. 1 is the diagram for . The relationship between with is given by
- .
Each multiplet is represented by a rectangular set of states centered at in this diagram. The number of states in the multiplet is . Illustrated is the multplet . All states of a multiplet share the same eigenvalue of and . The lowest corner in the multiplet is where . One can generate all states of a multiplet by starting from its lowest corner and repeatly operate on it with (which increases ) and with (which increases ). Obviously integer. Notice that for fixed and , there are in general a large number of multiplets , except for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \{\frac{M}{2}, 0\}} and , each of which occurs only once. For the former, the lowest corner is the point where which is a single state. For the later, the lowest corner is B where , which is also a single state.
References
[1] "η pairing and off-diagonal long-range order in a Hubbard model" C.N.Yang, Phys. Rev. Lett. 63, 2144–2147 (1989) [1]
[2] " Symmetry in a Hubbard Model" C.N.Yang, Mod. Phys. Lett. B4 (1990) 759-766
[3] "New Approach to the Theory of Superexchange Interactions" P. W. Anderson, Phys. Rev. 115, 2 (1959) [2]
[4] "Theory of Ferromagnetism and the Ordering of Electronic Energy Levels" E. Lieb and D.C. Mattis, Phys. Rev. 125, 164 (1962) [3]
[5] "Field Theories of Condensed Matter Systems" E. Fradkin, Addson-Wesley Redwood City (1991)