Midterm 2 Solutions: Difference between revisions
No edit summary |
|||
| Line 1: | Line 1: | ||
==Problem 1== | ==Problem 1== | ||
'''Consider a magnetic system described by an Ising model <math>(S_i = \pm1)</math> on a square lattice with <math>\ H = \sum_{\langle ij\rangle} J_{ij} s_i s_{j} + \sum_{\langle ij\rangle} K_{ij} s_i s_{j} </math>. Here, the ferromagnetic interaction <math> \ J_{ij} < 0 </math> couples only nearest-neighbor spins. In contrast,the antiferromagnetic interaction <math>\ K_{ij}>0 </math> couples only the the second neighbors, i.e. spins that are "across the square" ( diagonally placed relative to each other). | '''Consider a magnetic system described by an Ising model <math>(S_i = \pm1)</math> on a square lattice with <math>\ H = \sum_{\langle ij\rangle} J_{ij} s_i s_{j} + \sum_{\langle ij\rangle} K_{ij} s_i s_{j} </math>. Here, the ferromagnetic interaction <math> \ J_{ij} < 0 </math> couples only nearest-neighbor spins. In contrast,the antiferromagnetic interaction <math>\ K_{ij}>0 </math> couples only the the second neighbors, i.e. spins that are "across the square" ( diagonally placed relative to each other).''' | ||
===a)=== | |||
'''Sketch the suare lattice and determine the number of first neighbors <math>\Z_{FM}</math> which interact ferromagnetically with the given spin, and the number of second neighbors <math>\Z_{AFM}</math> which interact antiferromagnetically with the given spin. (5points)''' | |||
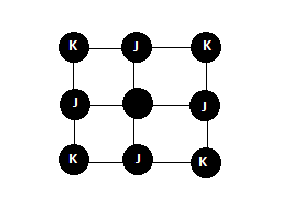
[[Image:lattice.png]] | [[Image:lattice.png]] | ||
Image of square lattice with ferromagnetic <math>J_{i,j} <0</math> coupling nearest neighbor spins. | Image of square lattice with ferromagnetic <math>J_{i,j} <0</math> coupling nearest neighbor spins. | ||
| Line 9: | Line 14: | ||
<math>Z_{AFM} =4</math> | <math>Z_{AFM} =4</math> | ||
b) | ===b)=== | ||
'''Use the mean-field approximation, where <math>\ S_{i} S_{j} \rightarrow S_{i} \langle S_{j} \rangle</math>. Assume that the magnitude of <math>\ J_{ij}</math> is appreciably larger then the magnitude of <math>\ K_{ij}</math>; then the system will order ferromagnetically at low temperatures, so that <math>\langle S_{i} \rangle = m </math> for any site. Derive the self consistency condition determining the magnetization "m". (15points)''' | |||
==Problem 2== | ==Problem 2== | ||
Revision as of 17:14, 7 April 2011
Problem 1
Consider a magnetic system described by an Ising model Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (S_i = \pm1)} on a square lattice with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ H = \sum_{\langle ij\rangle} J_{ij} s_i s_{j} + \sum_{\langle ij\rangle} K_{ij} s_i s_{j} } . Here, the ferromagnetic interaction Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ J_{ij} < 0 } couples only nearest-neighbor spins. In contrast,the antiferromagnetic interaction Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ K_{ij}>0 } couples only the the second neighbors, i.e. spins that are "across the square" ( diagonally placed relative to each other).
a)
Sketch the suare lattice and determine the number of first neighbors Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Z_{FM}} which interact ferromagnetically with the given spin, and the number of second neighbors Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Z_{AFM}} which interact antiferromagnetically with the given spin. (5points)
Image of square lattice with ferromagnetic Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle J_{i,j} <0}
coupling nearest neighbor spins.
Anti-ferromagnetic Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle K_{i,j} <0}
coupling only second nearest neighbors.
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z_{FM} =4}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z_{AFM} =4}
b)
Use the mean-field approximation, where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ S_{i} S_{j} \rightarrow S_{i} \langle S_{j} \rangle} . Assume that the magnitude of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ J_{ij}} is appreciably larger then the magnitude of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ K_{ij}} ; then the system will order ferromagnetically at low temperatures, so that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle S_{i} \rangle = m } for any site. Derive the self consistency condition determining the magnetization "m". (15points)
Problem 2
b) Since Coulomb interactions are long range by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e^2/r} high densities cause the formation of solids such as crystals.
f) where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T \rightarrow \infty}