Solution to Set 3

Ferromagnetism

Ferromagnetic ordering of microscopic magnets (the magnetic moments of individual particles).

This assignment corresponds to Section 8.3 and 8.4 in the Solid State Physics book. It deals with the topics of Magnetic Order, ferromagnetism, the Weiss molecular field.

Given Information

• Classical Ising antiferromagnet on a ”bipartite” lattice given by Hamiltonian Failed to parse (syntax error): {\displaystyle H = \frac{J}{2} \sum_{<ij>} S_i S_j -− h\sum_i S_i } ,

• Bipartite lattice: a lattice with 2 sublattices, so that each spin on sublattice A interacts only with some spin on the other sublattice B. In an antiferromagnetic state, each sublattice assumes a uniform magnetization.

• Magnetization for Lattice A: $m_{A}=<S^{(A)}>$

• Magnetization for Lattice B: $m_{B}=<S^{(B)}>$

• Average magnetization: $m={\frac {1}{2}}(m_{A}+m_{B}),$

• "Staggered” magnetization: $m^{\dagger }={\frac {1}{2}}(m_{A}-m_{B}),$ (Note: It's the difference between the two sublattices)

• $m=1\;$ for perfect ferromagnetic order

• $m^{\dagger }=1$ for perfect antiferromagnetic order

Part 1

Use Weiss mean-field decoupling to replace one of the spins in the Hamiltonian by its thermal average. The Weiss field experienced by a given spin is then proportional to the sublattice magnetization on the other sublattice. Write down self-consistent equations for $m_{A}\;$ and $m_{B}\;$, and express them through the order parameters $m\;$ and $m^{\dagger }$.

The Weiss Molecular Field

Chapter 8.3.1 of Solid State Physics The systematic way of replacing the spin operator in the Heisenberg Hamiltonian by their average values in order to obtain the Weiss molecular field approximation is to insert $S_{i}=<S>+(S_{i}-<S>)$ and $S_{j}=<S>+(S_{j}-<S>)$ into Failed to parse (syntax error): {\displaystyle H = \frac{J}{2} \sum_{<ij>} S_i S_j -− h\sum_i S_i }

The answer becomes $H\approx {\frac {1}{2}}\lambda \mu _{0}{\textbf {M}}^{2}-\sum _{i}\lambda \mu _{0}\mu _{i}{\textbf {M}}$

where

• $\lambda ={\frac {2\sum _{j\neq i}\jmath _{ij}}{N\mu _{0}g^{2}\mu _{b}^{2}}}$
• $\mu _{i}=-g\mu _{b}{\textbf {S}}_{i}$

Part 2

Assume that $h=0\;$, so that $m=0\;$, and solve the mean-field equations by expanding in $m^{\dagger }$. Determine the Neel (ordering) temperature, and calculate the order-parameter exponent.

The Néel Temperature

Chapter 8.4 of Solid State Physics

$T_{N}={\frac {C\lambda }{2}}$

where

• $T_{N}\;$ is Néel Temperature, the onset temperature for antiferromagnetism
• $C={\frac {N\mu _{0}g^{2}\mu _{b}^{2}}{k_{B}}}$ is Curie constant
• $\lambda ={\frac {4\sum _{j\neq i}\jmath _{ij}}{N\mu _{0}g^{2}\mu _{b}^{2}}}=-{\frac {4z\jmath }{N\mu _{0}g^{2}\mu _{b}^{2}}}$

Part 3

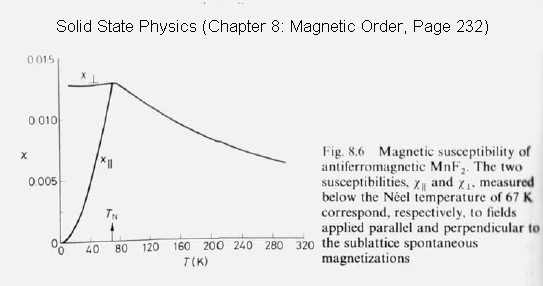
Now consider a small external field $h>0\;$, so that both order parameters can assume a nonzero value (Note: $m\;$ will be small). By keeping only the leading terms in $h\;$ and $m\;$, calculate the uniform spin susceptibility $\chi =\partial m/\partial h$, as a function of temperature. Plot $\chi \;$ as a function of temperature, and show that it has a cusp around $T_{N}\;$.

Part 4

Imagine adding a ”staggered” external field $h^{\dagger }$, which would be positive on sublattice A, but would be negative on sublattice B. Concentrate on the system with no uniform field $(h=0)\;$, and determine the behavior of the staggered susceptibility $\chi ^{\dagger }=\partial m^{\dagger }/\partial h^{\dagger }$. Show that $\chi ^{\dagger }$ blows up at the Neel temperature.