Solution to Set 5

I have no idea what I'm doing - KimberlyWynne 03:11, 2 March 2009 (EST)

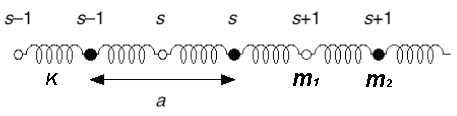
Diatomic harmonic chain

Problem 1

Given:

• a chain of atoms
• with alternating masses $m_{1}\;$ and $m_{2}\;$
• connected with elastic springs with constant $K\;$
• moving only in the x-direction

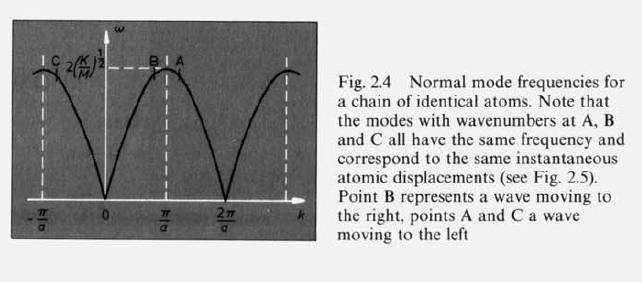
Derive the dispersion relation $\omega ^{\alpha }(k)\;$ for this chain

• Index $\alpha =1\;$ for acoustic branch

Potential Energy $U=1,2,3,...n\;$

$U\cong {\frac {1}{2}}k\sum _{n}(U_{n}-U_{n-1})\;$

$\Rightarrow m{\ddot {U}}_{n}=-k[2U_{n}-U_{n-1}-U_{n+1}]=-m\omega U(t)\;$

Eigenvectors of Modes A and B (defined arbitrarily)

$u_{m}(t)=e^{i\omega t}u_{m}\;$

$\Rightarrow -m\omega ^{2}{\ddot {\vec {u}}}_{n}=-k\mathbf {M} {\vec {u}}\;$

Band Matrix

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{M} = \begin{vmatrix} 2 & 1 & 0 & 0\\ 1 & 2 & 1 & 0\\ 0 & 1 & 2 & 1\\ 0 & 0 & 1 & 2 \end{vmatrix} }

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u_m (t) = e^{ik(na)- \omega t} = e^{i k R_n} \;}

where

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u_m \rightarrow u_n e^{ik(na)} \;}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle R_n \;} = distance on some coordinate system

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Rightarrow -m \omega ^2 \vec{u} = - k [2 - e^{ik \alpha} - e^{-ik \alpha}] \;}

Derive and get:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Rightarrow \omega (k) = 2 \sqrt{ \frac{k}{m} } |sin(ka)|}

• IndexFailed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha = 2\;} for optical branch

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u(R_n) \equiv e^{i k R_n} = cos (k a) \;<> <math>u_m (t) = e^{ik(na)- \omega t} = e^{i k R_n} \;}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Rightarrow - m \omega^2 e^{ikna} = -k [2e^{ik(na)} - e^{ik(n+1)a} - e^{ik(n-1)a}] \;}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Rightarrow m \omega^2 = k [2 - (e^{ika} + e^{-ika}] \;}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Rightarrow \omega^2 = \frac{2k}{m} [1 - cos(ka)] \;}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Rightarrow \omega^2 = \frac{\Delta k}{m} \frac{1}{2} [1 - cos(ka)] \;}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Rightarrow \omega^2 = \frac{\Delta k}{m} sin^{2}(\frac{ka}{2}) \;}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Rightarrow \omega (k) = 2 \sqrt{ \frac{k}{m} } |sin(\frac{ka}{2})| \;}

Problem 2

Determine the speed of sound for this chain. What is the lowest frequency of long-wavelength sound corresponding to the optical branch?

From my lecture notes: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega _{\alpha }(k)\approx C_{\alpha } k \;}

where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C_{\alpha } } = speed of sound

Problem 3

Sketch the motion of the atoms corresponding to the edge of the Brillouin zone, both for the optical and the acoustic branch.

Problem 4

Determine the Debye temperature for this system, and determine the form of the specific heat Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c_V (T)} in the limits of high and low temperatures.

Problem 5

Consider low temperatures (Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T \ll T_D\;} ) and determine the wavelength of the most abundant phonons Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda_{max}} (Hint: note the analogy with Wien's Law!)