Solution to Set 5: Difference between revisions
| Line 63: | Line 63: | ||
<math>\Rightarrow m \omega^2 = k [2 - (e^{ika} + e^{-ika}] \;</math> | <math>\Rightarrow m \omega^2 = k [2 - (e^{ika} + e^{-ika}] \;</math> | ||
<math>\Rightarrow \omega^2 = \frac{2k}{m} [1 - cos(ka)] = | <math>\Rightarrow \omega^2 = \frac{2k}{m} [1 - cos(ka)] \;</math> | ||
<math>\Rightarrow \omega^2 = \frac{\Delta k}{m} \frac{1}{2} [1 - cos(ka)] \;</math> | |||
<math>\Rightarrow \omega^2 = \frac{\Delta k}{m} sin^{2}(\frac{ka}{2}) \;</math> | |||
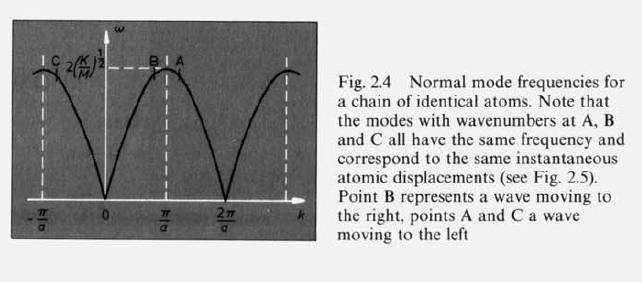
<math>\Rightarrow \omega (k) = 2 \sqrt{ \frac{k}{m} } |sin(\frac{ka}{2})| \;</math> | |||
[[Image:Dispersionrelation.jpg]] | [[Image:Dispersionrelation.jpg]] | ||
Revision as of 05:52, 2 March 2009
I have no idea what I'm doing - KimberlyWynne 03:11, 2 March 2009 (EST)
Diatomic harmonic chain
Problem 1
Given:
- a chain of atoms
- with alternating masses and
- connected with elastic springs with constant
- moving only in the x-direction
Derive the dispersion relation for this chain
- Index for acoustic branch
Potential Energy
Eigenvectors of Modes A and B (defined arbitrarily)
Band Matrix
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{M} = \begin{vmatrix} 2 & 1 & 0 & 0\\ 1 & 2 & 1 & 0\\ 0 & 1 & 2 & 1\\ 0 & 0 & 1 & 2 \end{vmatrix} }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u_m (t) = e^{ik(na)- \omega t} = e^{i k R_n} \;}
where
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u_m \rightarrow u_n e^{ik(na)} \;}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle R_n \;} = distance on some coordinate system
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Rightarrow -m \omega ^2 \vec{u} = - k [2 - e^{ik \alpha} - e^{-ik \alpha}] \;}
Derive and get:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Rightarrow \omega (k) = 2 \sqrt{ \frac{k}{m} } |sin(ka)|}
- IndexFailed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha = 2\;} for optical branch
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u(R_n) \equiv e^{i k R_n} = cos (k a) \;<> <math>u_m (t) = e^{ik(na)- \omega t} = e^{i k R_n} \;}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Rightarrow - m \omega^2 e^{ikna} = -k [2e^{ik(na)} - e^{ik(n+1)a} - e^{ik(n-1)a}] \;}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Rightarrow m \omega^2 = k [2 - (e^{ika} + e^{-ika}] \;}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Rightarrow \omega^2 = \frac{2k}{m} [1 - cos(ka)] \;}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Rightarrow \omega^2 = \frac{\Delta k}{m} \frac{1}{2} [1 - cos(ka)] \;}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Rightarrow \omega^2 = \frac{\Delta k}{m} sin^{2}(\frac{ka}{2}) \;}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Rightarrow \omega (k) = 2 \sqrt{ \frac{k}{m} } |sin(\frac{ka}{2})| \;}
Problem 2
Determine the speed of sound for this chain. What is the lowest frequency of long-wavelength sound corresponding to the optical branch?
From my lecture notes: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega _{\alpha }(k)\approx C_{\alpha } k \;}
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C_{\alpha } } = speed of sound
Problem 3
Sketch the motion of the atoms corresponding to the edge of the Brillouin zone, both for the optical and the acoustic branch.
Problem 4
Determine the Debye temperature for this system, and determine the form of the specific heat Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c_V (T)} in the limits of high and low temperatures.
Problem 5
Consider low temperatures (Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T \ll T_D\;} ) and determine the wavelength of the most abundant phonons Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda_{max}} (Hint: note the analogy with Wien's Law!)







![{\displaystyle \Rightarrow m{\ddot {U}}_{n}=-k[2U_{n}-U_{n-1}-U_{n+1}]=-m\omega U(t)\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/461b812664679855fe2267f3b2cb29ec477ba6b6)