Mott metal-insulator transition and magnetism: Difference between revisions
No edit summary |
No edit summary |
||
| Line 6: | Line 6: | ||
* Gravitational force | * Gravitational force | ||
* Magnetic force | * Magnetic force | ||
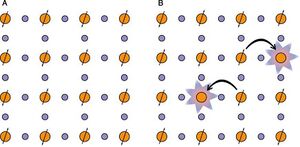
[[Image:doping cartoon.jpg|thumb|Fig. 2. The orange circles represent Cu atoms. In A, there is a one spin half state at every vertex. However, B shows after some spins are removed, allowing for the hopping of electrons]] | |||
For high <math>T_c</math> cuprate superconductors, the most studied are those with immediately adjacent Cu-O planes. This is due to the agreed upon (by both theorists and experimentalists) notion that charge transport and superconductivity are both in the CuO2 planes. For these Cu02 planes, electron hopping from Cu to Cu is prevented due to strong Coulomb repulsion. | |||
This coupled with the fact that an anti-ferromagnetic order is energetically favorable leads to the dominating electronic state being an anti-ferromagnetic '''Mott Insulator''' (as shown in Fig 2A). In order to allow for electrons to hop between Cu and Cu, some spins must be removed from these sites (as shown in Fig 2B). | |||
Through this process, the insulating <math>CuO_2</math> layer becomes doped with holes or electrons, yielding new electronic ordered states; one of these states being high <math>T_c</math> superconductivity. | |||
As previously mentioned, the properties and characteristics of these high <math>T_c</math> superconductors differ from conventional superconductors. The s-wave pairing symmetry exhibited by the conventional superconductors is absent in these high <math>T_c</math> cuprates, for which the pairing symmetry is <math>dx^2-y^2</math> symmetry. | |||
This is not the only notable difference between the two. The short coherence length, highly anisotropic critical current, and very high critical field are all different as well. One significant thing to note is that the length scales of these characteristics are all very similar in high <math>T_c</math> cuprates (~1 nm), while they often very by orders of magnitude in usual metals. Specifically: | |||
* the Fermi wavelength is ~1 nm | |||
* the Cu-Cu distance is ~.38 nm | |||
* the inter-dopant atomic distance ~1.5 nm | |||
* the superconducting coherence length is ~1-2 nm. | |||
Theorists and experimentalists agree that these distances suggest that different electronic phenomena can interact strongly with each other. | |||
Revision as of 07:34, 30 April 2009
The explanation of the nature of the Mott-Hubbard metal-insulator transition, i.e., the transition between a paramagnetic metal and a paramagnetic insulator driven by electronic interactions, is one of the classic and fundamental problems in condensed matter physics
Animal Magnetism
Action at a distance
- Coulomb forces and charges
- Gravitational force
- Magnetic force
For high cuprate superconductors, the most studied are those with immediately adjacent Cu-O planes. This is due to the agreed upon (by both theorists and experimentalists) notion that charge transport and superconductivity are both in the CuO2 planes. For these Cu02 planes, electron hopping from Cu to Cu is prevented due to strong Coulomb repulsion.
This coupled with the fact that an anti-ferromagnetic order is energetically favorable leads to the dominating electronic state being an anti-ferromagnetic Mott Insulator (as shown in Fig 2A). In order to allow for electrons to hop between Cu and Cu, some spins must be removed from these sites (as shown in Fig 2B).
Through this process, the insulating layer becomes doped with holes or electrons, yielding new electronic ordered states; one of these states being high superconductivity.
As previously mentioned, the properties and characteristics of these high superconductors differ from conventional superconductors. The s-wave pairing symmetry exhibited by the conventional superconductors is absent in these high cuprates, for which the pairing symmetry is symmetry.
This is not the only notable difference between the two. The short coherence length, highly anisotropic critical current, and very high critical field are all different as well. One significant thing to note is that the length scales of these characteristics are all very similar in high cuprates (~1 nm), while they often very by orders of magnitude in usual metals. Specifically:
- the Fermi wavelength is ~1 nm
- the Cu-Cu distance is ~.38 nm
- the inter-dopant atomic distance ~1.5 nm
- the superconducting coherence length is ~1-2 nm.
Theorists and experimentalists agree that these distances suggest that different electronic phenomena can interact strongly with each other.