Charge Density Wave

Introduction

Charge Density Wave (CDW) is a spatial modulation of the conduction electron density in a metal and an associated modulation of the lattice atom positions. In the relation to the symmetry breaking, CDW is a broken symmetry state of metals brought by the electron-phonon interactions whose ground states are the coherent superposition of electron-hole pairs, and it displays spatial variation.

CDW states was first discussed by Frohlich in 1954 and by Peierls in 1955. The latter pointed out that a one-dimensional metal coupled to the underlying lattice is not stable at low temperatures. The ground state of the coupled electron-phonon system is characterized by a gap in the single-particle excitation spectrum and by a collective mode formed by electron-hole pairs involving a wave vector $q=2k_{F}\!$ with the charge density $\rho ({\vec {r}})=\rho _{0}+\rho _{1}cos(2{\vec {k_{F}}}\cdot {\vec {r}}+\phi )$, where $\rho _{0}\!$ is the unperturbed electron density of the metal and the condensate is called the charge density wave. As with the superconductivity, CDW has a complex order parameter $\Delta e^{i\phi }\!$ with the magnitude of $\Delta \!$ determines the size of the electronic gap and the amplitude $\delta u\!$ of the atomic displacements. The phase $\phi \!$ determines the position of the CDW relative to the underlying lattice.

Materials

CDW primarily exists in the low-dimensional metals, that is metals whose Fermi surfaces exhibit high anisotropy (metal is defined as an object in which the Fermi surface exists). This anisotropy is the answer to the question why the conductivity along one axis is higher than it is in any other axis, hence although the material itself appears to be 3 dimensional, the conductivity exist only on a certain plane or a certain axis. The materials are typically conducting polymers, or also known as synthetic metals.

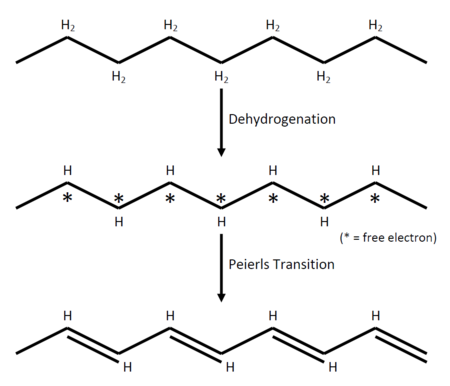
As a simple picture of how the CDW comes into the system, let's consider a thought experiment about making a polyacetylene out of polyethylene (although not so realistic) as shown in figure 1.

Figure 1. Dehydrogenating a polyethylene

This configuration with many free electrons is unstable because, of course, energetically unfavoured. For now, let's assume it is possible to make such a reaction and hold it "stable" for a while for observation. What we have after dehydrogenating the polyethylene is basically a metal (just looking at the free electrons). That being a metal, as we shall see later exhibits the so called nesting of the Fermi surface which gives rise to many interesting phenomena in the low dimensional metals, for example Kohn anomaly, Peierls transition, and density waves. Peierls transition deforms the lattice and an alternation of the double and single bonds will occur, producing polyacethylene.

(add polyacethylene picture here)

The double bonds is, naturally, stronger than the single bonds which results in the double bonds being shorter than the single bonds. The difference in the bond length implies that the charge density changes when one is moving along the axis. The alternation of the bonds gives the spatial variation.

Therefore, with this rather oversimplified picture, we see how the CDW develops and how some other phenomenon play their part.

Density Of States (DOS) of a 1-D Electron Gas (1DEG)

Fermi surface of a 1DEG consists of 2 sheets with a distance $2k_{F}\!$ apart, located at $\pm k_{F}$. The k-space DOS for 1DEG is just $L/2\pi \!$ and the number of states is $L/2\pi \times 2k_{F}=Lk_{F}/\pi \!$. The 2 orientations of the spin, when taken into account, gives a factor of 2, so the total number of states (or the number of electrons) is : $N={\frac {2Lk_{F}}{L}}$

And the Fermi wave vector is $k_{F}={\frac {N\pi }{2L}}$

The Fermi energy is ${\mathcal {E}}_{F}={\frac {\hbar ^{2}}{2m}}k_{F}^{2}={\frac {\hbar ^{2}}{2m}}\left({\frac {N\pi }{2L}}\right)^{2}\!$

The density of states of one spin is

${\begin{aligned}n({\mathcal {E}})&={\frac {L}{2\pi }}\int dk\delta \left({\mathcal {E}}-{\frac {\hbar ^{2}k^{2}}{2m}}\right)\\&={\frac {L}{2\pi }}\sum _{i=1}^{2}\int dk{\frac {\delta \left(k-{\sqrt {\frac {2m{\mathcal {E}}}{\hbar ^{2}}}}\right)}{\left|{\frac {\hbar ^{2}k_{i}}{m}}\right|}}\\&={\frac {L}{2\pi }}\left|{\frac {m}{\hbar ^{2}k}}\right|\\&={\frac {L}{\pi \hbar }}{\sqrt {\frac {m}{2{\mathcal {E}}}}}\end{aligned}}\!$

The result of our calculation shows that

1. We have $k_{F}={\frac {N\pi }{2L}}\!$ if N = 2 we will have a full band. Therefore $k_{F}=\pi /L\!$ gives an insulator (or intrinsic semiconductor). At this point, we shall consider $n<2/L$ so the system is metallic. Periodic potential contribution will be considered later.

2. The DOS is proportional to $E^{1/2}$, while it is constant and proportional to $E^{1/2}\!$ in the 2D and 3D system, respectively. Therefore, some quantities having a factor $dn({\mathcal {E}})/d{\mathcal {E}}\!$ changes sign going from 3D to 1D.

3. 1DEG Fermi wave vector $k_{F}~n\!$, while in 2D and 3D it is proportional to $n^{1/2}\!$ and $n^{1/3}\!$, respectively.

4. When the electron changes state by interacting with phonons, the only possible transition is from $k_{F}\!$ to $-k_{F}\!$ and vice versa by the conservation of energy and momentum.

Response Function of One-Dimensional Electron Gas (1DEG)

Electron in a material is attracted to the ions and feels repulsive force from any other electrons. As the result, in many-electron system there will be a spatial variation of the charge or known also as screening. One common example is electron will attract positive charged particles and creates a surplus of positive charge surrounding it and screens its field. Therefore we write the total charge density as a sum of the external (initial) and the induced charge density.

$\rho ({\vec {r}})=\rho _{ext}({\vec {r}})+\rho _{ind}({\vec {r}})\!$

From the theory of the dielectric media, the external potential is assumed to be linearly related to the total physical potential

$\phi ^{ext}({\vec {r}})=\int dr'\epsilon ({\vec {r}}-{\vec {r'}})\phi ({\vec {r'}})\!$

By using the Fourier transformation we can write this in the k-space as

$\phi ^{ext}({\vec {q}})=\epsilon ({\vec {q}})\phi ({\vec {q}})\!$

And the induced charge density satisfies the relation

$\rho ^{ind}({\vec {q}})=\chi ({\vec {q}})\phi ({\vec {q}})\!$

By using the perturbation theory and assuming linear response only, we get

INSERT THE STEPS FROM A&M HERE

$\chi ({\vec {q}})=-e^{2}\int {\frac {d^{D}k}{(2\pi )^{D}}}{\frac {f_{\vec {k}}-f_{\vec {k+q}}}{\epsilon _{\vec {k}}-\epsilon _{{\vec {k}}-{\vec {q}}}}}\!$

Now consider T = 0 (Lindhard response function), we see that each term does no vanish only when either $\epsilon _{\vec {k}}<\epsilon _{F}\!$ and $\epsilon _{{\vec {k}}+{\vec {q}}}>\epsilon _{F}\!$ (or to say that $f_{\vec {k}}=1\!$ and $f_{{\vec {k}}+{\vec {q}}}=0$) or the opposite. What it means is the nonvanishing value comes from the electron-hole pairs (occupied-unoccupied states).

Now by evaluating the integral (for 1D case)

$\chi (q)=-{\frac {e^{2}}{2\pi }}\int _{k_{F}}^{k_{F}}dk{\frac {1}{{\frac {-\hbar ^{2}}{2m}}(2kq+q^{2})}}\!$

The resulting prefactor is not that important, we are interested in the q dependence of the result, which is.

$\chi (q)\propto ln\left|{\frac {q+2k_{F}}{q-2k_{F}}}\right|\!$

INSERT PICTURE OF \CHI vs Q HERE