Notes 2: Difference between revisions
No edit summary |
No edit summary |
||
| Line 6: | Line 6: | ||
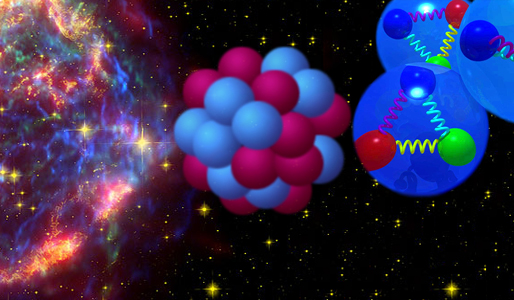
Atomic nuclei sizes are on the scale of <math>10^{-14} </math> meters and form the (relatively) small centers of atoms while carrying most of the mass. The basic constituents of atomic nuclei are protons and neutrons. Protons and neutrons are comprised of three quarks each, fundamental particles on a size scale of <math> 10^{-19} m </math>. The relevant interactions on these size/mass scales are the electro-weak and strong forces. The quarks in a nucleon are | Atomic nuclei sizes are on the scale of <math>10^{-14} </math> meters and form the (relatively) small centers of atoms while carrying most of the mass. The basic constituents of atomic nuclei are protons and neutrons. Protons and neutrons are comprised of three quarks each, fundamental particles on a size scale of <math> 10^{-19} m </math>. The relevant interactions on these size/mass scales are the electro-weak and strong forces. The quarks in a nucleon are | ||
==Definitions for Abundance== | |||
The particle abundance of isotope <math> i </math> is defined as | |||
:<math> | |||
X_{i} = \frac{n_i}{\sum_j n_j} \, | |||
</math> | |||
where <math> n_i </math> is the the number density of particle <math> i </math>, and the sum is taken over all isotopes present. It is also useful to define a relative particle abundance, which is set logarithmically and normalized to the abundance of hydrogen: | |||
:<math> | |||
\epsilon_i = \log_{10} X_i + 12 \ . | |||
</math> | |||
The mass fraction is the fraction of total mass in the sample constituted by species <math> i </math>: | |||
:<math> X_i = \frac{m_i}{m_{tot}} = \frac{m_i n_i}{\rho} \approx \frac{A_i n_i}{\rho N_A} </math> ( Note that <math> m_i \approx A_i m_u \ </math> and <math> m_u = \frac{m_{12C}}{12} = \frac{1}{N_A} </math> ) | |||
Denoting <math> Y_i\,</math> the mass per baryon, as | |||
:<math> | |||
Y_i \equiv \frac{X_i}{A_i} , | |||
</math> | |||
allows us to define the particle's number density by the density of the sample and this baryon fraction, | |||
:<math> | |||
n_i = Y_i \rho N_A \ . | |||
</math> | |||
Another useful quantity is the average mass number, or mean molecular weight, defined by | |||
:<math> | |||
\mu_i = \frac{\sum_i{A_i Y_i}}{\sum_i{Y_i}} = \frac{\sum_i{N_i}}{\sum_iY_i} = \frac{1}{\sum_i{Y_i}}</math> | |||
The electron abundance | |||
:<math> Y_e = \sum_i Z_i Y_i \ </math> , which can also be written as <math>Y_e = \frac{\sum_i{Z_i Y_i}}{\sum_i{A_i Y_i}} ,</math> | |||
is the ratio of protons to nucleons in the sample, and similarly to nuclei, the electron number density is found by | |||
:<math> | |||
n_e = Y_e \rho N_A \ . | |||
</math> | |||
Revision as of 18:40, 23 January 2011
Nuclear Astrophysics is a combination of nuclear physics and astrophysics. Nuclear physics is the study of atomic nuclei, their composition and their interactions, while astrophysics aims at studying galactic objects such as stars and galaxies. Nuclear astrophysics delves into the questions of where and when the elements were created and how nuclear reactions drive cosmic events.
The Nucleus
Atomic nuclei sizes are on the scale of meters and form the (relatively) small centers of atoms while carrying most of the mass. The basic constituents of atomic nuclei are protons and neutrons. Protons and neutrons are comprised of three quarks each, fundamental particles on a size scale of . The relevant interactions on these size/mass scales are the electro-weak and strong forces. The quarks in a nucleon are
Definitions for Abundance
The particle abundance of isotope is defined as
where is the the number density of particle , and the sum is taken over all isotopes present. It is also useful to define a relative particle abundance, which is set logarithmically and normalized to the abundance of hydrogen:
The mass fraction is the fraction of total mass in the sample constituted by species :
- ( Note that and )
Denoting the mass per baryon, as
allows us to define the particle's number density by the density of the sample and this baryon fraction,
Another useful quantity is the average mass number, or mean molecular weight, defined by
The electron abundance
- , which can also be written as
is the ratio of protons to nucleons in the sample, and similarly to nuclei, the electron number density is found by