Notes 3

Nuclear Astrophysics

Supernova Pathline

Nuclear Astrophysics is a multidisciplinary field of modern physics which concerns most notably the studies of Nuclear Physics and Astrophysics. Nuclear Astrophysics involves many different branches of physics dealing with the "very small" (Quantum Mechanics, Electrodynamics and Atomic Modeling) to the "very large" (General and Special Relativity, stellar life-cycles and compositions, Galactic formations/constructions and space-time/gravitational effects), and everything in between (such as Statistical/Thermal Mechanics, Kepler Orbits, and Newtonian Mechanics approximations).

Some of the most important subject matters of Nuclear Astrophysics involve element origins and abundances, high energy physics, nuclear reactions and corresponding rates, universal studies (from the Big-Bang model and early universe to the subsequent evolution and expansion of our universe) all the way to structural and chemical modeling of various astronomical objects such as black holes, neutron stars, pulsars, stars, nebulae and supernovae. Nuclear Astrophysics is perhaps one of the most comprehensive and involved branches of modern physics in that it deals with the widest variety of sub-fields within the discipline.

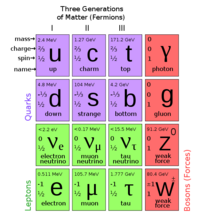
Atomic Structure

The Standard Model of Elementary Particles

Atoms are the basic units of matter, and are comprised of electrons, protons, and neutrons. The protons and neutrons are the densest part of the atom, and located in the nucleus. Electrons orbit this nucleus in quantized energy levels.

Electron

An electron is a subatomic particle with negative charge that orbits the nucleus in an atom. The electron is classified as a lepton. It interacts through the gravitational, electromagnetic, and weak forces.

Nucleus

The nucleus constituents protons and neutrons. The atomic nucleus can be denoted by $_{Z}^{A}X_{N}$, where $Z$ denotes the number of protons in the nucleus or atomic number, $N$ denotes the number of neutrons, $A$ denotes the number of nucleons or mass number, and $X$ denotes the element symbol.

Particle Abundances

One of the most important aspects of Nuclear Astrophysics is being able to calculate elemental abundances in astronomical structures. Particle abundances are given by:

$X_{i}={\frac {n_{i}}{\Sigma _{j}{n_{j}}}}$

Where the mass fraction $X_{i}$ is the fraction of total mass of a sample that is made up by a nucleus of species "i".

$n_{i}={\frac {X_{i}\times \rho }{m_{i}}}$

Where ${m_{i}}$ is the mass of the nucleus of species "i" and rho the corresponding mass density.

Determination of solar abundances

Earth Material

Problem: chemical fractionation modified the local composition strongly compared to pre solar nebula and overall solar system. For example, Quarz is 1/3 Si and 2/3 Oxygen and not much else. This is not the composition of the solar system. But, isotopic compositions mostly unaffected (as chemistry is determined by number of electrons (protons), not the number of neurons).

Solar Spectra

Sun formed directly from presolar nebula - (largely) unmodified outer layers create spectral features.

Unfractionated meteorites

Certain classes of meteorites formed from material that never experienced high pressure or temperatures and therefore was never fractionated. These meteorites directly sample the presolar nebula

Limits of Classical Mechanics

An image showing the double slit experiment.

When dealing with very small or quickly moving objects, the normal, classical laws of physics break down. With the advent of Quantum Mechanics, however, many stellar processes are more easily understood. Quantum Mechanics began to formulate in the early twentieth century, as scientists investigated the composition of atoms, and gained a better understanding of the properties of light. Famous experiments like the double-slit experiment demonstrated a need for a new theory to pick up where classical mechanics broke down. For example, an application of classical physics would predict that an electron would spiral inward towards the nucleus of the atom, whereas quantum theory proposes the Pauli-exclusion principle which dictates discrete energy levels, or steps, that the electron must be contained in. Major players in advancing quantum theory were Niels Bohr, Werner Heisenberg, Max Planck, Louis de Broglie, Albert Einstein, Erwin Schrödinger, Paul Dirac, Wolfgang Pauli, and many, many others.

Schrödinger Wave Function

Hamiltonian Mechanics present the energy of a particle as the sum of it's kinetic and potential energy;

$E=T+V={\frac {p^{2}}{2m}}+V$

One can apply the following substitutions for p, momentum, and E, energy:

$\displaystyle {p\rightarrow {\frac {\hbar }{i}}{\frac {d}{dx}}}$

$\displaystyle {E\rightarrow i\hbar {\frac {d}{dt}}}$

Which results in the following equation for a one-dimensional particle:

$i\hbar {\frac {\partial }{\partial t}}\psi (x,t)=\left[-{\frac {\hbar ^{2}}{2m}}{\frac {\partial ^{2}}{\partial x^{2}}}+V(x,t)\right]\psi (x,t)$