Superconducting Applications in Quantum Computation

Superconducting materials could potentially be used to implement a quantum computer, a device that utilizes quantum mechanical properties to produce significantly more powerful processors than we could possibly create in a classical computer. Typically, classical computers are composed of macroscopic integrated circuits made of semi-conducting materials, which are limited by classical mechanics. A quantum computer would be capable of accessing bit states unavailable to classical bits, making them exponentially more powerful.

Background

Bloch sphere depicting the states accessible to a qubit.

Computers perform computations using bits, a fundamental unit of information that is either in the state 1 or 0. One bit may not be particularly powerful but many bits can hold a lot of information; a string of n bits can be in any one of $2^{n}$ states. A quantum computer would significantly increase computational power by allowing each bit to occupy 1, 0, or any superposition of those two states. This strange phenomenon is possible due to the laws of quantum mechanics, which allow the states of the quantum bits - or qubits - to be transformed in a special way.

An easy way to understand the difference between a classical computer and a quantum computer is to look at a picture of a Bloch Sphere. Imagining the north pole of the sphere to correspond to the 1 state and the south pole to correspond to the 0 state, it's clear that a vector from the sphere's origin (representing a bit state) could only point along the z-axis in a classical computer. In a quantum computer, that vector could point to the 1 state or the 0 state along the z-axis but also to any other point on the sphere, representing the possible superpositions of the 1 and 0 states. This idea is summarized in the following formula for n qubits:

$\left|\psi \right\rangle =\sum _{i}^{2^{n}}\alpha _{i}\left|\varphi \right\rangle _{i}$

where $\varphi$ represents an allowed state and $\alpha$ is its probability coefficient. This can be simplified for a single qubit as:

$\left|\psi \right\rangle =\alpha \left|0\right\rangle +\beta \left|1\right\rangle$

where $\alpha$ and $\beta$ are complex numbers referred to as amplitudes, whose modulus squared gives the probability of the qubit being in the states $\left|1\right\rangle$ and $\left|0\right\rangle$ respectively.

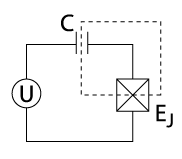
The Josephson Effect

The Josephson Effect is a phenomenon that occurs when two superconducting materials are separated by a thin layer of a non-superconducting material. This setup is consequently known as a Josephson Junction. Josephson Junctions may be useful in the future as quantum computational devices because of the quantum mechanical behavior that they exhibit under correct conditions.

DC Josephson Effect

The DC Josephson Effect refers to the current that arises due to cooper pair tunneling between the two superconducting materials. The current is given by

${\frac {}{}}I(t)=I_{c}\sin(\phi (t))$

where $I(t)$ is the current across the junction, $I_{c}$ is the critical current, and $\phi (t)$ represents the phase difference across the Josephson Junction (the phase difference between the two wave-functions that describe the cooper pairs that reside in the left and right sides). Below the critical current, there will be no voltage drop and zero resistance across the junction.

AC Josephson Effect

The AC Josephson Effect refers to the fact that the voltage across the junction is dependent on the derivative of the phase with respect to time. This relationship is given by

$U(t)={\frac {\hbar }{2e}}{\frac {\partial \phi }{\partial t}}$

where $U(t)$ represents the voltage across the junction, ${\frac {\hbar }{2e}}$ is the magnetic flux quantum, and $\phi (t)$ is the phase difference across the junction. When the current exceeds the critical current, the voltage is no longer zero. Instead, it oscillates in time.

Superconducting Qubits

There are three types of superconducting qubits, each of which depend on a different attribute to determine the computational state of the system.

Charge Qubits

The dotted line represents the Cooper-pair box.

Charge qubits predictably derive their states from charge states. They are composed of a Cooper-pair box coupled to a superconducting reservoir by a Josephson Junction. The state of a charge qubit is determined by the number of Cooper pairs that have tunneled across the junction, which is measured by a very sensitive electrometer.

Superconducting Quantum Interference Devices

SQUIDs may potentially be used to implement a quantum computer.