Superconducting Applications in Quantum Computation

Superconducting materials could potentially be used to implement a quantum computer, a device that utilizes quantum mechanical properties to produce significantly more powerful processors than we could possibly create in a classical computer. Typically, classical computers are composed of macroscopic integrated circuits made of semi-conducting materials, which are limited by classical mechanics. A quantum computer would be capable of accessing bit states unavailable to classical bits, making them exponentially more powerful.

Background

Bloch sphere depicting the states accessible to a qubit.

Computers perform computations using bits, a fundamental unit of information that is either in the state 1 or 0. One bit may not be particularly powerful but many bits can hold a lot of information; a string of n bits can be in any one of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2^n} states. A quantum computer would significantly increase computational power by allowing each bit to occupy 1, 0, or any superposition of those two states. This strange phenomenon is possible due to the laws of quantum mechanics, which allow the states of the quantum bits - or qubits - to be transformed in a special way.

An easy way to understand the difference between a classical computer and a quantum computer is to look at a picture of a Bloch Sphere. Imagining the north pole of the sphere to correspond to the 1 state and the south pole to correspond to the 0 state, it's clear that a vector from the sphere's origin (representing a bit state) could only point along the z-axis in a classical computer. In a quantum computer, that vector could point to the 1 state or the 0 state along the z-axis but also to any other point on the sphere, representing the possible superpositions of the 1 and 0 states. This idea is summarized in the following formula for n qubits:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left | \psi \right \rangle = \sum_{i}^{2^{n}} \alpha_{i} \left | \varphi \right \rangle_{i}}

where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \varphi} represents an allowed state and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha} is its probability coefficient. This can be simplified for a single qubit as:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left | \psi \right \rangle = \alpha \left | 0 \right \rangle + \beta \left | 1 \right \rangle }

where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha } and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta } are complex numbers referred to as amplitudes, whose modulus squared gives the probability of the qubit being in the states Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left | 1 \right \rangle } and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left | 0 \right \rangle } respectively.

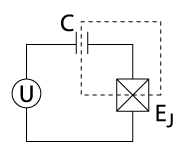
The Josephson Effect

The Josephson Effect is a phenomenon that occurs when two superconducting materials are separated by a thin layer of a non-superconducting material. This setup is consequently known as a Josephson Junction. Josephson Junctions may be useful in the future as quantum computational devices because of the quantum mechanical behavior that they exhibit under correct conditions.

DC Josephson Effect

The DC Josephson Effect refers to the current that arises due to cooper pair tunneling between the two superconducting materials. The current is given by

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{}{} I(t) = I_c \sin (\phi (t))}

where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I(t)} is the current across the junction, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I_c} is the critical current, and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi(t)} represents the phase difference across the Josephson Junction (the phase difference between the two wave-functions that describe the cooper pairs that reside in the left and right sides). Below the critical current, there will be no voltage drop and zero resistance across the junction.

AC Josephson Effect

The AC Josephson Effect refers to the fact that the voltage across the junction is dependent on the derivative of the phase with respect to time. This relationship is given by

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U(t) = \frac{\hbar}{2 e} \frac{\partial \phi}{\partial t}}

where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U(t)} represents the voltage across the junction, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\hbar}{2e}} is the magnetic flux quantum, and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi(t)} is the phase difference across the junction. When the current exceeds the critical current, the voltage is no longer zero. Instead, it oscillates in time.

Superconducting Qubits

There are three types of superconducting qubits, each of which depend on a different attribute to determine the computational state of the system.

Charge Qubits

The dotted line represents the Cooper-pair box.

Charge qubits predictably derive their states from charge states. They are composed of a Cooper-pair box coupled to a superconducting reservoir by a Josephson Junction. The state of a charge qubit is determined by the number of Cooper pairs that have tunneled across the junction, which is measured by a very sensitive electrometer.

Flux Qubits

Flux qubits are composed of a loop of superconducting material connected to a number of Josephson Junctions. The difference between a flux qubit and a charge qubit is that while in a charge qubit the charging energy dominates the coupling energy, the reverse is true for a flux qubit. The high ratio of coupling energy to charging energy in a flux qubit allows cooper pairs to move continuously around the superconducting loop instead of tunneling across junctions as they do in a charge qubit. The computational state of the flux qubit is determined by the direction of the current that flows through the loop. This may seem to model a classical bit, but the flux qubit can reach a "quantum" state by manipulating the applied flux (hence, "flux qubit"). When the applied flux is close to a half-integer multiple of flux quanta, the energy levels which correspond to the two directions of circulating current are brought close together and loop may be used as a qubit.

Phase Qubits

A Phase Qubit is yet another superconducting device that utilizes Josephson Junctions to simulate a qubit.

Superconducting Quantum Interference Devices

SQUIDs may potentially be used to implement a quantum computer.