Phy5645: Difference between revisions

From PhyWiki
Jump to navigation Jump to search
Line 102: Line 102:


                                               <math>{\lim}\limits_{x \to -\infty}V(x)=V_-              {\lim}\limits_{x \to +\infty}V(x)=V_+</math>
                                               <math>{\lim}\limits_{x \to -\infty}V(x)=V_-              {\lim}\limits_{x \to +\infty}V(x)=V_+</math>
    and assuming that:    eq=V_-<V_+
    Schrodinger equation:
                                                  eq=[-\frac{\hbar^2}{2m}\frac{d^2}{dx^2}+V(x)]\psi(x)=E\psi(x)
                                        eq=\rightarrow \frac{d^2}{dx^2}\psi(x)+\frac{2m}{\hbar^2}(E-V(x))\psi(x)=0
    From this equation we can discuss some general properties of 1-D motion as follows:
    If eq=E>V_+:
    eq=E-V(x)>0 at both eq=-\infty and eq=+\infty. Therefore, the solution of Schrodinger equation are trigonometric function (sine or cosine). The wave function is oscillating at both eq=-\infty and eq=+\infty. The particle is in unbound state. The energy spectrum is continous. Both oscillating solutions are allowed, the energy level are two-fold degenerate.
    If eq=V_-\le E \le V_+:
    eq=E-V(x)>0 at eq=-\infty but eq=E-V(x)<0 at eq=+\infty. Therefore, the wave function is oscillating at  eq=-\infty but decaying exponentially at eq=+\infty. The energy spectrum is still continous but no longer degenerate.
    If eq=E<V_-:
    eq=E-V(x)<0 at both eq=-\infty and eq=+\infty. Therefore, the wave function decays exponentially at both eq=-\infty and eq=+\infty. The particle is in bound state. The energy spectrum is discrete and non-degenerate.
    * 1D bound states
    Infinite square well
    Let's consider the motion of a particle in an infinite and symmetric square well: eq=V(x)=+\infty for eq=x \ge L/2,  otherwise  eq=V(x)=0
    A particle subject to this potential is free everywhere except at the two ends (eq=x = \pm L/2), where the infinite potential keeps the particle confined to the well.  Within the well the Schrodinger equation takes the form:
                                 
    or equivalently,
                                          where     
    Writing the Schrodinger equation in this form, we see that our solution are those of the simple harmonic oscillator:
                                 
    Now we impose that the solution must vanish at eq=x = \pm L/2:
                                        eq=-Asin(kL/2)+Bcos(kL/2)=0
                                          eq=Asin(kL/2)+Bcos(kL/2)=0
    Adding the two equation, we get:
                                    eq=Bcos(kL/2)=0
    It follows that either eq=B=0 or eq=cos(kL/2)=0.
    Case 1: eq=B=0.
    In this case eq=A\ne0, otherwise the wavefunction vanishes every where. Furthermore, it is required that:
              eq=sin(kL/2)=0    eq=\rightarrow k=2n\pi/L          where    eq=n=1,2,3,...
    And the wave functions are odd:
                                        eq=\psi(x)=Asin(2n\pi x/L)
    Case 2: eq=cos(kL/2)=0  eq=\rightarrow k=(2n+1)\pi/L  where    eq=n=0,1,2,...
    In this case eq=A=0 and eq=B\ne0, and the wavefunctions are even:
                                        eq=\psi(x)=Bcos[(2n+1)\pi x/L]
    Parity operator and the symmetry of the wavefunctions
    In the above problem, two basic solutions of Schrodinger equation are either odd or even. The general wavefunctions are combinations of odd and even functions. This properties originates from the fact that the potential is symmetric or invariant under the inversion eq=x \rightarrow -x, and so does the Hamiltonian. Therefore, the Hamiltonian commutes with the parity operator eq=\bold p (eq=\bold p \psi(x)=\psi(-x)). In this case, the wavefunctions themselves do not need to be odd or even, but they must be some combinations of odd and even functions.
    Non-degeneracy of the bound states
    Let's consider a more general property that is the Wronskian for 2 solutions of the 1-D Schrodinger equation must equal to a constant.
    Schrodinger equation :
                                          eq=-\frac{\hbar^2}{2m}\frac{d^2\psi}{dx^2}+V(x)\psi=E\psi                          (1)
    is a second-order differential equation. Such equation has 2 linearly independent eq=\psi_E^{(1)} and eq=\psi_E^{(2)} for each value of eq=E:
                                          eq=-\frac{\hbar^2}{2m}\frac{d^2\psi_E^{(1)}}{dx^2}+V(x)\psi_E^{(1)}=E\psi_E^{(1)}                (2)
                                          eq=-\frac{\hbar^2}{2m}\frac{d^2\psi_E^{(2)}}{dx^2}+V(x)\psi_E^{(2)}=E\psi_E^{(2)}                (3)
    By definition in mathematics, the Wronskian of these functions is:
                                            eq=W=\psi_E^{(1)}\frac{d\psi_E^{(2)}}{dx}-\frac{d\psi_E^{(1)}}{dx}\psi_E^{(2)}                    (4)
    Multiplying equation (2) by eq=\psi_E^{(2)}, equation (3) by eq=\psi_E^{(1)}, then subtracting one equation from the other, we get:
                                            eq=\frac{d^2\psi_E^{(1)}}{dx^2}\psi_E^{(2)}-\frac{d^2\psi_E^{(2)}}{dx^2}\psi_E^{(1)}=0
                                    eq=\rightarrow \frac{d}{dx}(\frac{d\psi_E^{(1)}}{dx}\psi_E^{(2)}-\frac{d\psi_E^{(2)}}{dx}\psi_E^{(1)})=0
                                    eq=\rightarrow \frac{dW}{dx}=0
                                    eq=\rightarrow W=C                                                  (5)
    where eq=C is constant.
    So, the Wronskian for 2 solutions of the 1-D Schrodinger equation must equal to a constant.
   
    For the bound states, the wave function vanish at infinity, i.e:
                                          eq=\psi_E^{(1)}(\infty)=\psi_E^{(2)}(\infty)=0                          (6)
    From (4), (5) and (6), it follows that    eq=W=0                                    (7)
    From (4) and (7), we get:
                                          eq=\psi_E^{(1)}\frac{d\psi_E^{(2)}}{dx}-\frac{d\psi_E^{(1)}}{dx}\psi_E^{(2)}=0
                                    eq=\rightarrow \frac{1}{\psi_E^{(1)}}\frac{d\psi_E^{(1)}}{dx}-\frac{1}{\psi_E^{(2)}}\frac{d\psi_E^{(2)}}{dx}=0
                                    eq=\rightarrow \frac{d}{dx}[ln(\psi_E^{(1)})-ln(\psi_E^{(2)})]=0
                                    eq=\rightarrow ln(\psi_E^{(1)})-ln(\psi_E^{(2)})=constant
                                    eq=\rightarrow \psi_E^{(1)}=constant.\psi_E^{(2)}                                  (8)
    From (8) it follows that eq=\psi_E^{(1)} and eq=\psi_E^{(2)} describe the same state. Therefore, the bound states are non-degenerate.
    *
      Scattering states
The scattering states are those not bound, where the energy spectrum is a continuous band.  Unlike the bound case, the wave-function does not have to vanish at plus/minus infinity, though a particle can not reflect from infinity often giving a useful boundary condition.  At any changes in the potentials, the wave-function must still be continuous and differentiable as for the bound states.
For the delta function potential the derivative of the wave-function is not differential, but has a step.  Integrating the schrodinger wave equation from just one side of the step to just the other and then taking the limit as the difference between the integral limits becomes zero.
    *
      Oscillation theorem
      Let us concentrate on the bound states of a set of wavefunctions. Let  be an eigenstate with energy  and  an eigenstate with energy , and . We also can set boundary conditions, where both  and  vanish at .This implies that
       
       
        Subtracting the second of these from the first and simplifying, we see that
       
        If we now integrate both sides of this equation from  to any position x' and simplify, we see that
       
        The key is to now let x' be the first position to the right of  where  vanishes.
       
        Now, if we assume that  does not vanish at or between x' and , then it is easy to see that the left hand side of the previous equation has a different sign from that of the
        right hand side, and thus it must be true that  must vanish at least once between x' and  if .
    *
      Transmission-Reflection, S-matrix
    *
      Motion in a periodic potential
      An example of a periodic potential is given in Figure 1 which consists of a series of continuous repeating form of potentials. In other words, the potential is translationally symmetric over a certain period (in Figure 1 it is over period of a).
      Figure 1.
      The Hamiltonian of system under periodic potential commutes with the Translation Operator defined as:
     
     
     
     
      This means that there is a simultaneous eigenstate of the Hamiltonian and the Translation Operator. The eigenfunction to the Schrodinger Equation,
       
      has the form of the following,
     
      ,
      where,
      This result is also known as the Bloch Theorem.
     
      Also, by operating the  operator on the wavefunction (also known as the Bloch wave), it can be seen that this waveform is also an eigenfunction of the  operator, as shown in the following,
      Using the same argument, it is clear that,
     
      Also, note that if k is complex, then after multiple  operations, the exponential will "blow-up". Thus, k has to be real. Applying the Bloch Theorem in solving Schrodinger Equation with known periodic potential will reveal interesting and important results such as a band gap opening in the Energy vs k spectrum. For materials with weak electron-electron interaction, given the Fermi energy of the system, one can then deduce whether such a system is metallic, semiconducting, or insulating.
     
     
      Figure 1. Energy band illustration showing the condition for metal, semiconductor, and insulator.
     
     
      Consider for example the periodic potential and the resulting Schrodinger equation,
                                                                                 
Focusing the attention for case when 0 < x < a, the solution to the Schrodinger equation is of the form:
From periodicity,
Thus, the wavefunction from x < 0 (left) and x > 0 (right) can be written as:
When the continuity requirement at x = 0 is also being imposed, the following relation is found:
          (1)
From differentiability and periodicity, the Schrodinger equation can be solved as the following:
where  is small, approaching zero. In this case, the term on the right hand side can be taken to be 0. Thus,
where,
Evaluating further, the following condition is found:
              (2)
By simultaneously solving equation (1) and (2), the relationship between q and k is found to be:
 
                        (3)  .
Where q is the energy band of the system, and k is the accessible energy band. By noting that the maximum value of the LHS is < the maximum value of the RHS of the relation above, it is clearly seen that there are some energy level that are not accessible as shown in Figure 2.
Figure 2. Graph of Eq.(3). Wave is representing the LHS function, gray box representing the range of RHS function. Red lines is the forbidden solution, black line is the allowed solution.
As k increases from 0 to  , there will be many solutions. Focusing only to two of the allowed solutions, it is seen that as k increases, there will be two solutions (one solution gives increasing q value, the other solution gives decreasing q value). Using the fact that the energy of the system is  , the dispersion relation (E vs. k) can be plotted as shown in Figure 3.
Figure 3. Energy vs k showing the existence of band gap for system of an electron under periodic potential.
Thus, in conjunction with Pauli exclusion principle, the single particle banspectrum such as the one we discussed here constitutes a simple description of band
insulators and band metals.


== Operators, eigenfunctions, symmetry, and time evolution ==
== Operators, eigenfunctions, symmetry, and time evolution ==

Revision as of 12:43, 16 December 2008

Welcome to the Quantum Mechanics A PHY5645 Fall2008

Schrodinger equation. The most fundamental equation of quantum mechanics which describes the rule according to which a state Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\Psi\rangle} evolves in time.

This is the first semester of a two-semester graduate level sequence, the second being PHY5646 Quantum B. Its goal is to explain the concepts and mathematical methods of Quantum Mechanics, and to prepare a student to solve quantum mechanics problems arising in different physical applications. The emphasis of the courses is equally on conceptual grasp of the subject as well as on problem solving. This sequence of courses builds the foundation for more advanced courses and graduate research in experimental or theoretical physics.

The key component of the course is the collaborative student contribution to the course Wiki-textbook. Each team of students is responsible for BOTH writing the assigned chapter AND editing chapters of others.

Outline of the course:


Physical Basis of Quantum Mechanics

Basic concepts and theory of motion in QM

In Quantum Mechanics, all of the information of the system of interest is contained in a wavefunction , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Psi\,\!} . Physical properties of the system such as position, linear and angular momentum, energy, etc. can be represented via linear operators, called observables. These observables are a complete set of commuting Hermitian operators, which means that the common eigenstates (in the case of quantum mechanics, the wavefunctions) of these Hermitian operators form an orthonormal basis. Through these mathematical observables, a set of corresponding physical values can be calculated.

In order to clarify the paragraph above, consider an analogous example: Suppose that the system is a book, and we characterize this book by taking measurements of the dimensions of this book and its mass (The volume and mass are enough to characterize this system). A ruler is used to measure the dimensions of the book, and this ruler is the observable operator. The length, width, and height (values) from the measurements are the physical values corresponding to that operator (ruler). For measuring the weight of the book, a balance is used as the operator. The measured mass of the book is the physical value for the corresponding observable. The two observable operators (the ruler and the mass scale) have to commute with each other, otherwise the system can not be characterized at the same time, and the two observables can not be measured with infinite precision.

In quantum mechanics, there are some measurements that cannot be done at the same time. For example, suppose we want to measure the position of an electron. What we would do is send a signal (a gamma ray, for example), which would strike the electron and return to our detectors. We have, then, the position of the electron. But as the photon struck the electron, the electron gained additional momentum, so then our simultaneous momentum measurement could not be precise. Therefore both momentum and position cannot be measured at the same time. These measurement are often called "incompatible observables." This is explained in the Heisenberg uncertainty principle and implies, mathematically, that the two operators do not commute.

This concept contrasts with classical mechanics, where the two observables that do not commute with each other can still be measured with infinite precision. This is because of the difference in dimension of the object: macroscopic (classical mechanics) and microscopic scale (quantum mechanics). However, the prediction of quantum mechanics must be equivalent to that of the classical mechanics when the energy is very large (classical region). This is known as the Correspondence Principle, formally expressed by Bohr in 1923.

We can explain this principle by the following: In quantum mechanics, particles cannot have arbitrary values of energy, only certain discrete values of energy. There are quantum numbers corresponding to specific values of energy and states of the particle. As the energy gets larger, the spacing between these discrete values becomes relatively small and we can regard the energy levels as a continuum. The region where the energy can be treated as a continuum is what is called the classical region.

UV Catastrophy (Blackbody Radiation)

Imagine a perfect absorber cavity (i.e. it absorbs all radiation at all wavelengths, so that its spectral radiance is only going to depend on the temperature). This emission is called the blackbody radiation. This blackbody radiation experiment shows an important failure of classical mechanics. Lord Rayleigh (John William Strutt) and Sir James Jeans applied classical physics and assumed that the radiation in this perfect absorber could be represented by standing waves with nodes at the ends. The result predicts that the spectral intensity will increase quadratically with the increasing frequency, and will diverge to infinite energy or intensity squared at a UV frequency, or so called "Ultraviolet Catastophy."

In 1900, Max Planck offered a successful explanation for blackbody radiation. He also assumed the the radiation was due to oscillations of the electron, but the difference between his assumption and Rayleigh's was that he assumed that the possible energies of an oscillator were not continuous. He proposed that the energy of this oscillator would be proportional to the frequency of a constant, the Planck constant.

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E=h\nu=\hbar\omega}

Here E is energy, h is the Planck constant (Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle h=6.626*10^{-34} Joule-seconds \!} ) and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \nu\!} is the frequency of the oscillator. With the concept of energy being discrete in mind, the result is that Planck's calculation avoided the UV catastrophy, and instead the energy approached zero as the frequency is increased. In summary, the energy of the electromagnetic radiation is proportional to frequency instead of the amplitude of the electromagnetic waves, defying the classical physics where the energy is proportional to the intensity.

Photoelectric Effect

Consider a system composed of light hitting a metal plate. From experimental observations, a current can be measured as light is incident on the metal plate. This phenomenon was first studied by Albert Einstein (1905). During this period, the classical point of view is that an electron is bound inside of an atom, and an excitation energy is needed in order to release it from the atom. This energy can be brought forth in the form of light. The classical point of view also includes the idea that the energy of this light is proportional to its intensity. Therefore, if enough energy (light) is absorbed by the electron, the electron eventually will be released. However, this is not the case.

The determining factor here is not the intensity of the light, but the frequency used on the electron. If the frequency of the light is the "specific" frequency, the electron will be released. This specific frequency of light is in resonance with the energy "frequency" of the electron. Einstein made the conclusion that the energy of a single photon is proportional to its frequency, not the intensity.

Einstein realized that the classical view that light is a wave was not true, but instead light must be a particle. If light were a wave, then the mechanism that the wave transmits its energy is due to its perturbation, which is the amplitude of the wave. The photoelectric effect clearly shows that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (amplitude)^2 = intensity } has no affect on the electron energy, instead, only a specific frequency will have an effect on the energy of the electron. Agreeing with the UV catastrophy conclusions, he stated that light is made of particles called "photons," with an energy equal to hv.

Stability of Matter

One of the most important problems to inspire the creation of Quantum Mechanics was the model of the Hydrogen Atom. After Thompson discovered the electron, and Rutherford, the nucleus (or Kern, as he called it), the model of the Hydrogen atom was refined to one of the lighter electron of unit negative elementary charge orbiting the larger proton, of unit positive elementary charge. However, it was well known that classical electrodynamics required that charges accelerated by an EM field must radiate, and therefore lose energy. For an electron that moves in circular orbit about the more massive nucleus under the influence of the Coulomb attractive force, here is a simple non-relativistic model of this classical system:

Where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r\,\!} is the orbital radius, and we neglect the motion of the proton by assuming it is much much more massive than the electron.

So the question is: What determines the rate Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho} of this radiation? and how fast is this rate?

The electron in the Bohr's model involves factors of: radius Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r_0\,\!} , angular velocity Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega\,\!} , charge of the particle Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e\,\!} , and the speed of light, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c\,\!} : Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho=\rho(r_0,\omega,e,c)\,\!}

The radius and charge will not enter separately, this is because if the electron is far from the proton, then the result can only depend on the dipole moment, which is .

Therefore the above parameters is now:Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho(er_0, \omega, c) \!}

What are the dimensions of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho\,\!} ?

Essentially, since light is energy, we are looking for how much energy is passed in a given time: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [\rho]=\frac{energy}{time} \!}

Knowing this much already imposes certain constraints on the possible dimensions. By using dimensional analysis, let's construct something with units of energy.

From potential energy for coulombic electrostatic attractions: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle energy=\frac{e^2 }{length} \!}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e} has to be with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r_0} , multiply by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r^2} , and divide Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle length^2} .

The angular velocity is in frequency, so to get the above equations in energy/time, just multiply it with the angular velocity, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle energy=\frac{e^2 }{length}\frac{r^2}{length^2}*\omega }

(Here, it is seen that the acceleration of the electron will increase with decreasing orbital radius. The radiation due to the acceleration a is given by the Larmor Formula: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle energy \sim \frac{e^2r_0^2 }{(c/w)^3} w = \frac{e^2r_0^2 }{c^3}w^4\sim\frac{1}{r_0^4 } \!}

It was known that the hydrogen atom had a certain radius on the order of .5 angstroms. Given this fact it can easily be seen that the electron will rapidly spiral into the nucleus, in the nanosecond scale. Clearly, the model depicts an unstable atom which would result in an unstable universe. A better representation of of an electron in an atom is needed.

Double Slit Experiment

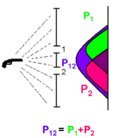
Bullet

Double slit thought experiment with classical bullets

Imagine a rattling gun which is shooting bullets in all directions. A histogram of the bullet's location after it passes through the two slits is plotted. If slit 2 is closed, but the slit 1 is open, then the green peak is observed which is given by the distribution function Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p_1} . Similarly, if the slit 1 is closed, but he slit 2 is open, the pink peak is observed which is given by the distribution function Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p_2} . When both slits are open, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle peak_{12}} (purple) is observed. This agrees with the classical view, where the bullet is the particle and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p_{12}} is simply a sum of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p_1} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p_2} .

The equation describing the probability of the bullet arrival if both of the slit are open is therefore

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p_{12}=p_1+p_2.}


Classical Waves

Double slit thought experiment with water waves


As waves are passed through the double slit, the intensity of the waves which are proportional to the squares of the height of the wave motion Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H1^2} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H2^2} are observed when slit 1 and 2 are closed respectively. These intensities are similar to the histograms for the bullets in the previous demonstration. However, an interference pattern of the intensity (Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H12} ) is observed when both slits are opened. This is due to constructive and destructive interferences of the two waves. The resultant interference is the square of the sum of the two individual wave heights Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H12 = (H1 +H2 )^2}

Stationary states and Heisenberg Uncertainty relations

Schrodinger equation and motion in one dimension

The time dependent Schrodinger equation is

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i\hbar \frac{\partial}{\partial t}|\psi\rangle=\mathcal{H}|\psi\rangle}

where the state Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\psi\rangle} evolves in time according to the Hamiltonian operator Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{H}} .

Motion in 1D

Overview

Let's consider the motion in 1 direction of a particle in the potential V(x). Supposing that V(x) has finite values when x goes to infinity 

                                             Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\lim}\limits_{x \to -\infty}V(x)=V_-              {\lim}\limits_{x \to +\infty}V(x)=V_+}

Operators, eigenfunctions, symmetry, and time evolution

Commutation relations and simulatneous eigenvalues

COMMUTATORS

The commutator of two operators A and B is defined as follows:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [A,B]=AB-BA\,\!.}

If Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [A,B]=0} , we say that the operators Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B} commute. Conversely, if , we say that the operators and do not commute. We can think of the commutator between two operators as a measure of how badly the two fail to commute.

Identities:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [A,B]+[B,A]=0 \!}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [A,A]= 0 \!}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [A,B+C]=[A,B]+[A,C]\!}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [A+B,C]=[A,C]+[B,C]\!}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [AB,C]=A[B,C]+[A,C]B\!}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [A,BC]=[A,B]C+B[A,C]\!}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [A,[B,C]]+[C,[A,B]]+[B,[C,A]]=0\!}



Some more complicated commutator identities can be found here http://sites.google.com/site/phy5645fall2008/some-useful-commutator-identites

COMPATIBLE OBSERVABLES

An operator which corresponds to some physically measurable property of a system is called an observable. All observables are Hermitian. If two Obersvables have simultaneous eigenkets, meaning for two obervables A and B,


Then we have that, also, .

So we can see that,

The same logic works in reverse. So if two observables, A & B commute, i.e. if , then they have simultaneous eigenkets, and they are said to be compatible observables. Conversely, if , we say that the operators and do not commute and are incompatible observables.


POSITION AND MOMENTUM OPERATORS An extremely useful example is the commutation relation of and . In 1D position space, = x and .

Applying , to an arbitrary state ket we can see that:



The position and momentum operators are incompatible. This provides a fundamental contrast to classical mechanics in which x and p obviously commute.

We can further generalize this relation between a position coordinate with its own and other conjugate momenta with what are known as the canonical commutation relations:




where the indices stand for x, y, or z.


CONNECTION BETWEEN CLASSICAL MECHANICS AND QUANTUM MEACHNICS

There is a wonderful connection between Classical mechanics and Quantum Mechanics. The Hamiltonian is a concept in the frame of classical mechanics. In this frame, the Hamiltonian is defined as:



There are two possibilities.

1. If the Lagrangian does not depend explicitly on time the quantity H is conserved. 2. If the Potential and the constraints of the system are time independent, then H conserves and also H is the Energy of the system.

It's clear from the above equation that:




This pair of the equations is called Hamilton's equations of motions. now let's define the following classical commutator:



This commutator is called Poisson Bracket, and it has interesting properties. To see, let's calculate commutation relationships between coordinates and momenta.






This relations clearly shows how close are the quantum commutators with classical world. If we perform the following identification:



Then we get quantum commutators. This identifications is called canonical quantization. As a final an important remark, the fact that we have classical commutators doesn't mean that we will have Heisenberg uncertainty relation for conjugate classical variables. This is because in classical mechanics the object of study are points (or body as a collection of points). In quantum mechanics we object of study is the state of a particle or system of particles - which describes the probability of finding a particle, and not it's exact, pointlike, location of momentum.


HAMILTONIAN

In Quantum Mechanics, an important property that one needs to check on a given operator (let's say ) is if it commutes with the Hamiltonian . If commutes with , then the eigenfunctions of can always be chosen to be eigenfunctions of . If commutes with the Hamiltonian and does not explicitly depend on time, then is a constant of motion.


COMMUTATORS & SYMMETRY

We can define an operator called the parity operator, which does the following:



The parity operator commutes with the Hamiltonian if the potential is symmetric, . Since the two commute, the eigenfunctions of the Hamiltonian can be written as eigenfunctions of the parity operator. This means that if the potential is symmetric, the solutions will be linear combinations of functions which have definite parity (even and odd functions).

GENERALIZED HEISENBERG UNCERTAINTY RELATION

Heisenberg and interaction picture: Equations of motion for operators

Feynman path integrals

Discrete eigenvalues and bound states. Harmonic oscillator and WKB approximation

Harmonic oscillator spectrum and eigenstates Coherent states Feynman path integral evaluation of the propagator Motion in magnetic field WKB

Angular momentum

Commutation relations, angular momentum as generator of rotations in 3D, eigenvalue quantization Orbital angular momentum eigenfunctions

Central forces

Free particle in spherical coordinates Hydrogen atom

Continuous eigenvalues and collision theory

Differential cross-section and the Green's function formulation of scattering Central potential scattering and phase shifts Born approximation and examples of cross-section calculations Coulomb potential scattering Two particle scattering

Retrieved from "http://wiki.physics.fsu.edu/index.php?title=Phy5645&oldid=126"