Electron-phonon interactions and Kohn anomalies

Electron-phonon interactions

The study of interactions between electrons and phonons, is an interesting and classical topic in quantum many body theory as well as condensed matter physics. The electron-phonon interaction leads to many novel properties in metals, for instance, electrical resistance, thermal resistance, superconductivity and the renormalization of linear electronic specific heat. [1]

Free electrons in lattice

In contrary to the independent electron model, where electrons experience weak periodic potential, the interaction of an electron with all other electrons and nuclei is represented by ‘effective potential’ in some average way, in the tight-binding approximation, electrons move in strong periodic potentials which cannot be approximated by an average background. In this situation, we can assume that the atoms are very widely separated and atomic orbitals remain undistorted.

As an example, the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H^+_2} problem will be revisited in the second quantization language. States Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |1>} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |2>} denote the states of electrons locate on atom 1 and 2, respectively. The state of the two-electron system is thus given by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |n_1, n_2>} , where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |n_i>} is the occupation number for each atom. Define creation and annihilation operators Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c^+_i} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c_i} , which obey anti-commutation relations:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left\{c_i, c^+_j\right\}=\delta_i,j} ,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left\{c_i, c_j\right\}=0} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left\{c^+_i, c^+_j\right\}=0} .

The Hamiltonian has the following form:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H=E_0(c^+_1c_1+c^+_2c_2)-t(c^+_1c_2+c^+_2c_1)}

Note that this Hamiltonian is non-diagonal. In order to diagonalize it, we could define the following bonding and anti-bonding operators:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c_B=1/\sqrt{2}(c_1+c_2)}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c_A=1/\sqrt{2}(c_1-c_2)}

Both bonding and anti-bonding operators obey anti-commutation relations. The Hamiltonian can be expressed by these operators as

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H=(E_0+t)c^+_Ac_A+(E_0-t)c^+_Bc_B}

The state of the system is thus given by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |n_A, n_B>} .

It is easy to generalize the above single molecule problem to electrons moving in crystal. Assume that the tight binding approximation is valid and only one atomic orbital (say, orbital A) is taken into consideration. Moreover, assume that only nearest neighbor hopping term is significant. The Hamiltonian of the system is given by

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H=E_A\sum_{i,\sigma}c^+_{i,\sigma}-t_A\sum_{<i,j>,\sigma}(c^+_{i,\sigma}c_{j,\sigma}+c^+_{j,\sigma}c_{i,\sigma})}

where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle <i,j>} means that the summation goes over only nearest neighbor sites. Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle R_i} is the site position and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c_{i,\sigma}} is the annihilation operator which destroys one electron in orbital A at site i with spin Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma} . Apply Fourier transformation on electron operator

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c_{\vec{p},\sigma}=\frac{1}{\sqrt{N}}\sum_{j} e^{i\vec{p}\cdot\vec{R_j}}c_{j,\sigma}}

The momentum Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{p}} is defined in the first Brillouin zone. Hence, the Hamiltonian can be written in terms of the operators in momentum space as

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H=\sum_{\vec{p},\sigma}E_{\vec{k}}c^+_{\vec{k},\sigma}c_{\vec{k},\sigma}}

Phonons: crystal vibrations

Lattice vibrations in a 3D crystal is a realistic model for the study of sound waves. Dynamics of lattice vibration generates phonon propagation in crystal. Let us first ignore the the discret properties of crystal and treat it as a continuous media. Let Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{u}(\vec{r})} be the displacement field which describes the elastic deformations of media. For small fluctuations, the kinetic energy is given by

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T=\frac{1}2\rho_0\int{d^3\vec{r}|\dot{\vec{u}}(\vec{r})|^2}}

where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho_0} is the mass density. The potential energy is given by

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V=\frac{1}2\rho_0\int{d^3\vec{r}}\{\Gamma_L(\vec{\nabla})^2+\Gamma_T\vec{\nabla}\times{\vec{u}}|^2\}}

The first term is from longitudinal contribution and the second term is from transverse contribution. However, these expressions are too crude to describe lattice vibrations in general.

If we abandon the ‘continuum’ frame and treat the crystal as a discrete lattice system, the Hamiltonian has the following form

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H=\sum_{j}\frac{P^2_j}{2M}+U(\vec{r}_1,…,\vec{r}_N)}

where j denotes the lattice sites and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{r}_j=\vec{R}_j+\vec{u}_j} . Assume that the adiabatic approximation is valid, due to the more massive nuclei than electrons. In this sense, the electrons could follow the movement of nuclei quite fast as if they are fixed on nuclei and move together. Within harmonic approximation, we could expand the potential energy U in Taylor series up to the second order:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U(\vec{r}_1,…,\vec{r}_N)=U(\vec{R}_1,…,\vec{R}_N)+\sum^{N}_{j=1}\vec{u}_j\cdot\vec{\nabla}_jU|_{\vec{r}=\vec{R}}+\frac{1}2\sum_{j,k}(\vec{u}_j\cdot\vec{\nabla}_j)(\vec{u}_k\cdot\vec{\nabla}_k)U|_{\vec{r}=\vec{R}}+\cdot\cdot\cdot }

Lattice Vibration and Phonons in 1D

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H^0_{ph} = \sum_{k \lambda}\hbar\omega_{k \lambda}( b^\dagger_{k \lambda} b_{k \lambda} + \frac{1}{2} )}

---

Acoustical and Optical Phonon in 3D

In moatomic Bravais lattice.

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U \approx U_0 + \frac{1}{2}\sum_{ \mathbf{R}^0_1 \mathbf{R}^0_2 } \sum_{\alpha\beta} u_\alpha ( \mathbf{R}^0_1) \frac{\partial^2 U}{\partial u_\alpha (\mathbf{R}^0_1) \partial u_\beta (\mathbf{R}^0_2) }|_{\mathbf{u}=0} u_\beta(\mathbf{R}^0_2) }

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H^0_{ph} = \sum_{\mathbf{k} \lambda} \hbar \omega_{\mathbf{k} \lambda}( a^\dagger_{\mathbf{k} \lambda} + \frac{1}{2} ), [a_{\mathbf{k} \lambda} , a^\dagger_{\mathbf{k} \lambda}] = \delta_{\mathbf{k,k^\prime}} \delta_{ \lambda , \lambda^\prime} }

Derivation of Hamiltonian Electron-Phonon Coupling

The Hamiltonian for the electron-phonon interaction can be described as

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H = H^0_{el} + H^0_{ph} + H_{coul} + H_{int}}

Where

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H^0_{el} = \sum_{k \sigma}E_k c^\dagger_{k \sigma} c_{k \sigma}}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H^0_{ph} = \sum_{k \lambda}\omega_{k \lambda}( a^\dagger_{k \lambda} + \frac{1}{2} )}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H_{coul} = \frac{1}{2} \sum_{k k^\prime q \atop \sigma \sigma^{\prime} } V(q)c^\dagger_{k ^\prime + q \sigma^\prime } c^\dagger_{k \sigma} c_{k+q \sigma} c_{k^{\prime} \sigma^{\prime}} }

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H_{int} = \sum_{k k^{\prime} \sigma \lambda} g_{k k^{\prime}} c^{\dagger}_{k+q \sigma} c_{k^{\prime} \sigma} ( b^\dagger_{-q \lambda} + b_{q \lambda} ) }

---

Jellium model

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V^{jel}_{el-ph} = \frac{1}{\nu} \sum_{\mathbf{k}\sigma}\sum_{\mathbf{q}}g^{jel}_{\mathbf{q}} }

Kohn anomalies

Screening

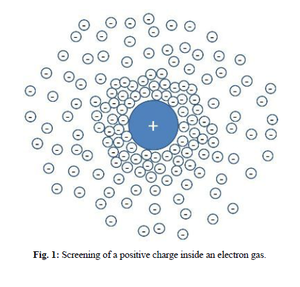
What is a free electron gas? A metal can be considered as an ionic lattice embedded inside an electron sea. The periodic ion lattice causes a periodic potential. In the free electron model we treat the ions as a uniform background of positive charge.

Screening is an important phenomena in a free electron gas. When an external positive charge density Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho_{\text{ext}} \left(\mathbf{\vec r}\right)} is applied, the electrons will be attracted to surround the positive charge (Fig. 1). The re-arrangement of the electrons generates an induced charge distribution Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho_{\text{el}} \left(\mathbf{\vec r}\right)} . Therefore, the total charge density Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho \left(\mathbf{\vec r}\right) } = Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho_{\text{ext}} \left(\mathbf{\vec r}\right)} + Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho_{\text{el}} \left(\mathbf{\vec r}\right)} is less positive than Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho \left(\mathbf{\vec r}\right) } . Thus, The total potential Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi \left(\mathbf{\vec r}\right) } is weaker than the external potential Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi_{\text{ext}} \left(\mathbf{\vec r}\right) } caused by the positive charge only. The phenomenon is called screening.

Kohn anomalies

the coupling function refers to the scattering of a quasi-particle from a point Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{k}_1} to a point Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{k}_2} in momentum space with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{p} = \mathbf{k}_1 - \mathbf{k}_2} . Energy and momentum conservation require that both $\mathbf {k} _{1}$ and $\mathbf {k} _{2}$ lie on the Fermi surface. This immediately introduces a restriction on the phonon wave vector $\mathbf {q}$: phonon wave vectors connecting nested parts of the Fermi surface will strongly interact with the electrons leading to a large phonon damping, whereas those which do not span the Fermi surface will not interact with electrons. Kohn pointed out that the interaction of phonons with the conduction electrons in a metal should cause anomalies in the phonon spectra.

$\mathbf {p} =\mathbf {k} _{1}-\mathbf {k} _{2}$