Bose Hubbard model: Difference between revisions
MattMartens (talk | contribs) |
JoeBelarge (talk | contribs) No edit summary |
||
| Line 37: | Line 37: | ||
Adjusting the potential depth via frequency variations allowed for Greiner et al. to essentially set the phase of the condensate. When they would set a potential, they would then turn it off. The atomic wavefunctions then expand freely and interfere with eachother. This allowed for a test of phase coherence of the system via diffraction patterns. | Adjusting the potential depth via frequency variations allowed for Greiner et al. to essentially set the phase of the condensate. When they would set a potential, they would then turn it off. The atomic wavefunctions then expand freely and interfere with eachother. This allowed for a test of phase coherence of the system via diffraction patterns. | ||
The phase was also tested by measuring the excitation spectrum of the condensate, as the superfluid state and the Mott insulator state should have markedly different spectrum's. | The phase was also tested by measuring the excitation spectrum of the condensate, as the superfluid state and the Mott insulator state should have markedly different spectrum's. In the Mott insulator phase the atoms are well localized in the lattice. An excitation occurs when a particle hole pair is created. For example if we had exactly one particle per lattice site, then an excitation would be when one particle tunnels to an adjacent site, creating a site with no particles and a site with two. | ||
=== Superfluid Phase === | === Superfluid Phase === | ||
For the superfluid phase it was expected to observe sharp diffraction patterns. This is due to the fact that in the superfluid phase all atoms are delocalized, with equal relative phases between different lattice sites. Therefore the sharp diffraction patterns represent extreme phase coherence in the system. | For the superfluid phase it was expected to observe sharp diffraction patterns. This is due to the fact that in the superfluid phase all atoms are delocalized, with equal relative phases between different lattice sites. Therefore the sharp diffraction patterns represent extreme phase coherence in the system. | ||
Revision as of 15:17, 14 December 2012
Introduction
The Bose-Hubbard Model (BHM) was first studied in detail in 1989 by Fisher et al.[1] They studied a three dimensional Bose gas in several different types of systems, including the most simple case at zero temperature. --> This is just an idea, I havent finished it yet, and dont know if it is necessary so let me know what you guys think about it.
Hamiltonian
Solving the Hamiltonian
The single site Hamiltonian for interacting bosons is:
Where and , are c-numbers.
In this case the Hamiltonian can be rewritten as:
.
Unnormalized eigenstates of this Hamiltonian are.
The normalized eigenstate is
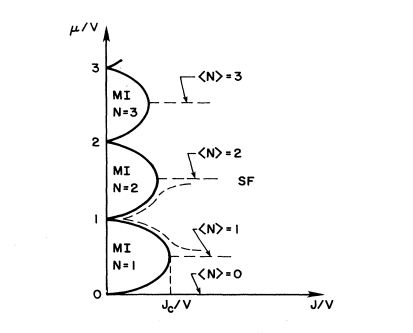
Phase Transition
Experimental Evidence - Bose-Einstein Condensate
Experimental Setup
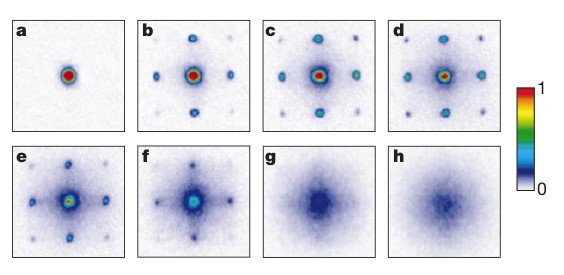
The first experimental evidence in support of the BHM was observed in 2002.[2]
Greiner and collaborators created a Bose-Einstein condensate that was spherically symmetric, and magnetically trapped. To form the three dimensional lattice potential three optical standing waves were set up perpendicular to eachother with the crossing point of the three beams positioned at the center of the condensate. The magnetically trapped condensate was then transferred to the optical lattice by slowly increasing the beam intensity. By increasing slowly it was ensured that the atoms stayed in the many body ground state. When the beams reached full intensity the condensate was spread over more than 150,000 lattice sites with an average of 2.5 atoms per lattice cite in the center of the condenstate
Adjusting the potential depth via frequency variations allowed for Greiner et al. to essentially set the phase of the condensate. When they would set a potential, they would then turn it off. The atomic wavefunctions then expand freely and interfere with eachother. This allowed for a test of phase coherence of the system via diffraction patterns.
The phase was also tested by measuring the excitation spectrum of the condensate, as the superfluid state and the Mott insulator state should have markedly different spectrum's. In the Mott insulator phase the atoms are well localized in the lattice. An excitation occurs when a particle hole pair is created. For example if we had exactly one particle per lattice site, then an excitation would be when one particle tunnels to an adjacent site, creating a site with no particles and a site with two.
Superfluid Phase
For the superfluid phase it was expected to observe sharp diffraction patterns. This is due to the fact that in the superfluid phase all atoms are delocalized, with equal relative phases between different lattice sites. Therefore the sharp diffraction patterns represent extreme phase coherence in the system.
Mott Insulator Phase
For the Mott insulator phase it was expected to have a blurred diffraction pattern. This is because the system should lose all phase coherence which will result in no observable diffraction pattern. It can be observed in figure 2 X that there is a clear loss of sharp diffraction patterns in box g, this corresponds to the onset of the Mott insulator phase.









