Phy5645/doubledelta

The potential is not affected by inversion. This implies that the wave functions have definite parity. The above potential is an attractive one. An attractive potential always has a ground state. The 1D space is divided into 3 regions. If we consider a particle with E<0, then in the leftmost and rightmost regions the wave function is of the type $Ae^{\left|-x\right|}$ and $De^{\left|-x\right|}$ respectively. The solution in the second region is $Be^{-\alpha x}+Ce^{\alpha x}$. For functions of even parity A=D, B=C. By continuity of wavefunction Ae^{-\alpha a}=Be^{-\alpha a}+Ce^{-\alpha a}. Integrating the Schrodinger equation from – ε to + ε and where ε tending to zero,

    ${\psi }'\left(a+\right)-{\psi }'\left(a-\right)={\frac {-2mg}{\hbar ^{2}}}\psi \left(a\right)$

Therefore,

               $\alpha e^{2\alpha a}={\frac {mg}{\hbar ^{2}}}\left(e^{2\alpha a}+1\right)$

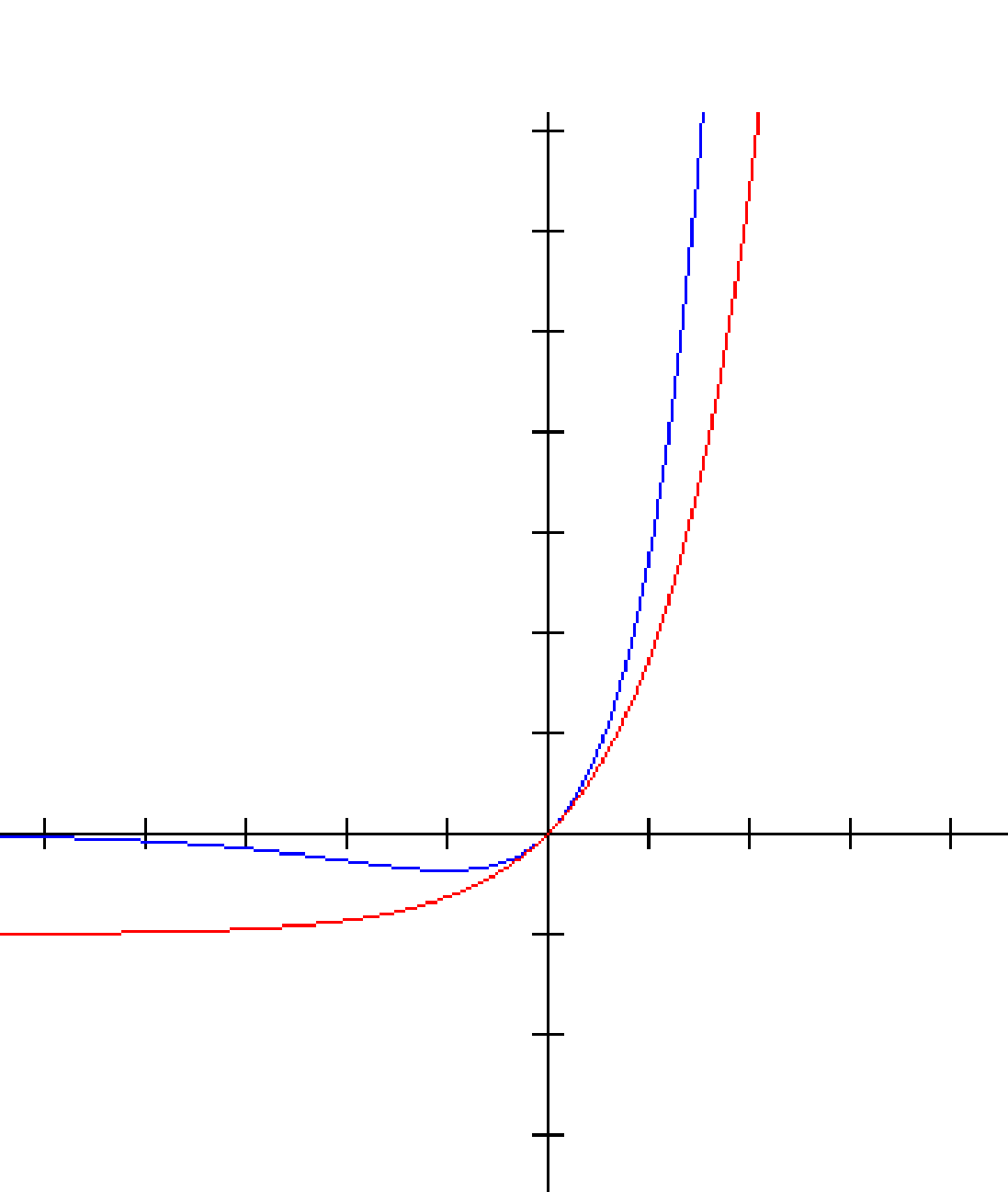
For function of odd parity, A= -D and B= -C. Using the same method as we followed above,we get

                $\alpha e^{2\alpha a}={\frac {mg}{\hbar ^{2}}}\left(e^{2\alpha a}-1\right)$

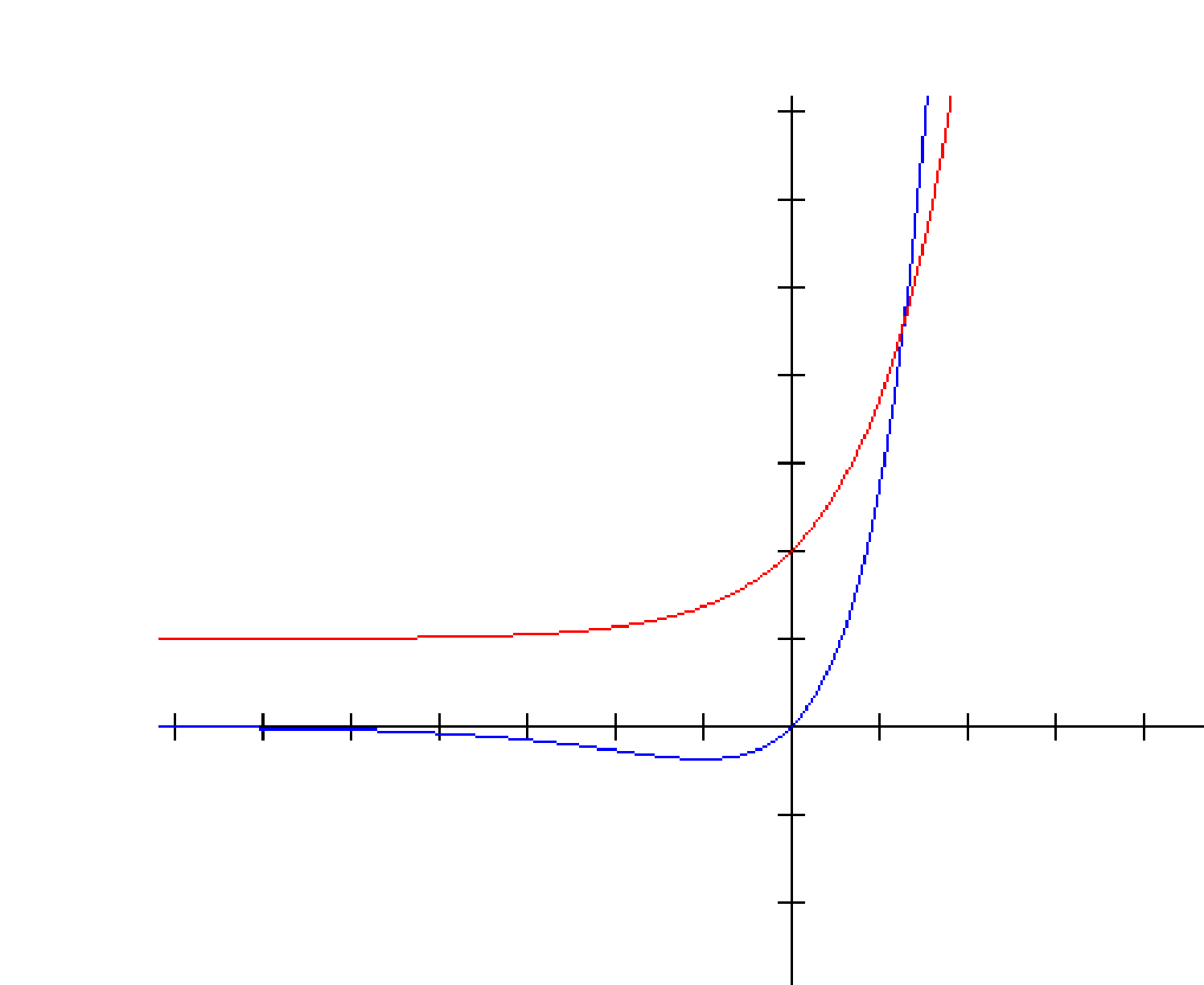
The first equation always has a solution whereas the second does not always have one. This is seen easily from the fact that for positive values of α, the right hand side of the second equation is zero only at the origin and increases slower than the left hand side (except if the coefficient is adjusted so that it increases faster in the beginning).

Blue: $xe^{x}$ Red: $e^{x}-1$

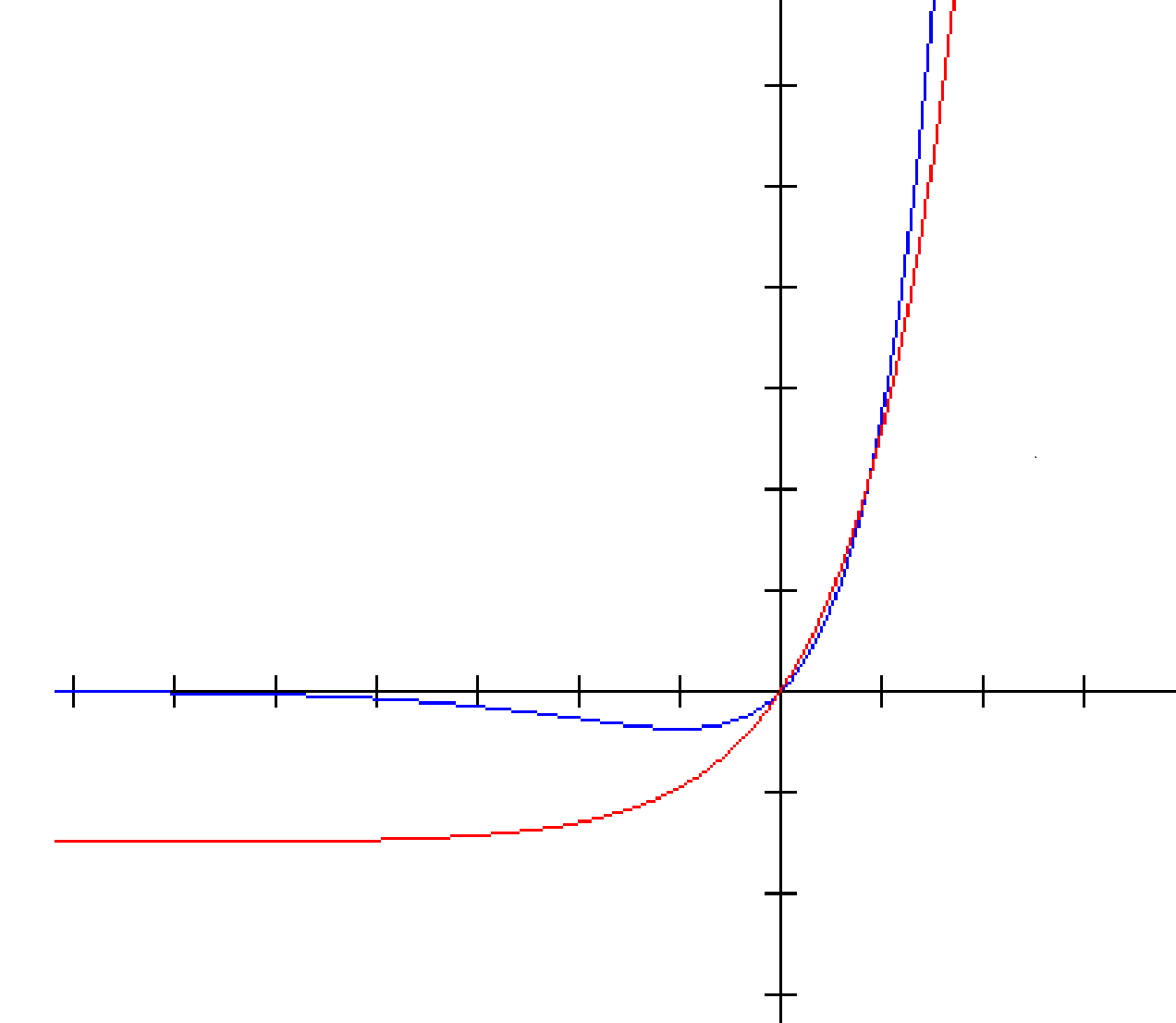
The blue is as before. The red curve corresponds to $1.5\left(e^{x}-1\right)$. On the other hand, for the first equation, when $\alpha =0$ , the right hand side is non-zero whereas the left hand side is zero. Yet, the right hand side increases slower. Therefore it shall be equal to the left hand side inevitably. Hence the state that always exists corresponds to the solution of the first equation. Hence that is the ground state.

The blue curve is $xe^{x}$. The red curve is $e^{x}-1$. Therefore the ground state has even parity. If the value of the separation is large enough (so that the right hand side increases faster than the left hand side), then the odd parity solution exists. Therefore the first excited state exists for large enough values of 2a.