2nd Week: Properties of Astrophysical Plasmas

The remnant of "Tycho's Supernova", a huge ball of expanding plasma.

Plasma is a state of matter in which the atoms and the molecules are so hot, that they have ionized into negatively charged electrons and positively charged ions. The plasma found in the universe, whose physical properties are studied in astrophysics is known as astrophysical plasma. To study the properties of astrophysical plasma the equation of state of matter is very important. Here, we will bring some basic tools from thermodynamics and derive the equation of state for non-relativistic and relativistic plasma.

Basic thermodynamics for quantum systems

The particle density is determined as follows

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n = \frac{N}{V} =\int_{0}^{\infty }{w(p)f(p)dp} \ , }

where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(p)} is the occupation probability and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle w(p)} is the state density per unit volume.

The energy density is given by

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u = \frac{U}{V} =\int_{0}^{\infty }{Ew(p)f(p)dp} \ , }

where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E} in the energy of the particle.

The pressure is defined as

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P = \frac{1}{3}\int_{0}^{\infty }{pvw(p)f(p)dp} \ , }

where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p} is the value of the momentum of the particle and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle v} is its velocity.

Distribution functions

In statistical physics the density of states of a system describes the number of states at each energy level that are available to be occupied. The general form of the density of state is as follows:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega(E) = \frac{d\Phi}{dE} \ , }

where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi} is the number of states.

For the non-relativistic system

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi(E) = \frac{4\pi}{3}\frac{g}{h^3}(2mE)^{3/2} \ , }

where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle g=2s+1} is the statistical weight. Then the density of state is

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega(E) = 2\frac{g}{h^3}(2mE)^{1/2} \ . }

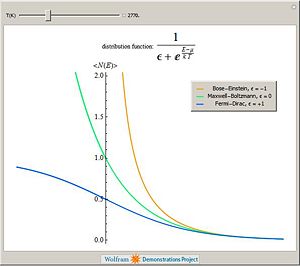
There are four probability distribution functions in statistical physics that are known with infinite support: Gibbs distribution, Maxwell-Boltzmann distribution, Fermi-Dirac distribution and Bose-Einstein distribution. The occupation probability, i.e. the probability of occupation of a given energy states are as follows.

• Maxwell-Boltzmann distribution

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(p)=e^{-\frac{E(p)-\mu}{kT}} \ , }

• Bose-Einstein distribution

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(p)=\frac{1}{e^{\frac{E(p)-\mu}{kT}}-1} \ , }

• Fermi-Dirac distribution

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(p)=\frac{1}{e^{\frac{E(p)-\mu}{kT}}+1} \ , }

where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k} is the Boltzmann constant.

Thermodynamical variables and potentials

Now we provide with the expressions of thermodynamic potentials. The internal energy is given by

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U = TS - PV + \sum_i \mu_i N_i \ , }

where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T} is the temperature, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S} is the entropy, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P} is the pressure and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V} is the volume of the system, while Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle N_i} is the number of particles in the state Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i} of the system and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu_i} is is the chemical potential associated to those particles. These quantities are also known as thermodynamical variables.

The so called Helmholtz free energy is given by

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F = U-TS \ . }

The enthalpy of the system can be found using the expression

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H = U+PV \ .}

The Gibbs free energy is

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G = U+PV -TS \ .}

The so called Landau potential is expressed by

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Omega = U-TS-\sum_i \mu_i N_i \ . }

Equation of state

Comparsion of the Fermi-Dirac, Bose-Einstein, and Boltzmann distributions. All for the same value Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu} .

In physics equations of state are thermodynamic equations that describe the state of matter under a given set of physical conditions. these equations provide relationships between two or more macroscopically measurable quantities (such as pressure, volume, temperature and Energy) in a given state of matter.

A classic example of an EOS is the Ideal Gas Law by Benoît Paul Émile Clapeyron

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\ pV = nRT} \ .}

Important Equations of State for Nuclear Astrophysics as given in class:

Particle density for a given system is

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n = \sum{n_i} \ , }

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n_i = \frac{4\pi g_i}{h^3}\int_{0}^{\infty }{\frac{p_i^2 dp_i}{exp[\frac{E_i-\mu_i}{kT}]\pm 1}} \ ,}

where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_i = \sqrt{p_i^2c^2 + (m_ic^2)^2}} in general.

Pressure for a given system is

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P = \sum{P_i} \ , }

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P_i = \frac{4\pi c^2g_i}{3h^3}\int_{0}^{\infty }{\frac{p_i^4 dp_i}{E_i(exp[\frac{E_i-\mu_i}{kT}]\pm 1)}} \ .}

Photon Gas

A photon is a particle viewed as an elementary form of radiation on the electromagnetic spectrum. Although, photons behave as both a particle and a wave so giving rise to particle-wave duality. They have integer spin,so being a boson. As a result must obey Bose-Einstein statistics.