Solution to Set 2

Part 1

First one is to find the isothermal compressibility of a Van der Waals gas for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T > T_c\;} .

The Van der Waals equation of state is: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(P + {N^2a \over V^2}\right) \left(V - Nb\right) = Nk_BT}

Solving this for P gives: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P = \left({Nk_BT \over V-Nb}\right) - {N^2a \over V^2}}

Then taking the partial derivative with respect to V at constant T: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left( {\partial P \over \partial V} \right)_T = -{ Nk_BT \over \left( {V-Nb} \right)^2 } + { 2N^2a \over V^3}}

Bringing the terms over a common denominator looks like: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left( {\partial P \over \partial V} \right)_T = {2N^2a \left( {V-Nb} \right)^2 - Nk_BTV^3 \over V^3 \left( {V-Nb} \right)^2} }

Then finding the negative reciprocal of this function gives the isothermal compressibility: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \kappa_T = -\left( {\partial V \over \partial P} \right)_T = - {1 \over {\left( {\partial P \over \partial V} \right)_T}} = {V^3 \left( {V-Nb} \right)^2 \over Nk_BTV^3 - 2N^2a\left( {V-Nb} \right)^2 } }

For those of you wondering why the 1/V is missing in the isothermal compressibility equation (it was added to the homework around 5 PM the day the homework was due and is there now), the answer is because it depends on the result desired. The formula used here to solve for the isothermal compressibility gives the total volume change per change in pressure. However, should that 1/V be kept it would give the fractional change in volume per change in pressure. For completeness, the result for the fractional isothermal compressibility is:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \kappa_T = -{1 \over V} \left( {\partial V \over \partial P} \right)_T = - {1 \over V} {1 \over {\left( {\partial P \over \partial V} \right)_T}} = {V^2 \left( {V-Nb} \right)^2 \over Nk_BTV^3 - 2N^2a\left( {V-Nb} \right)^2 } }

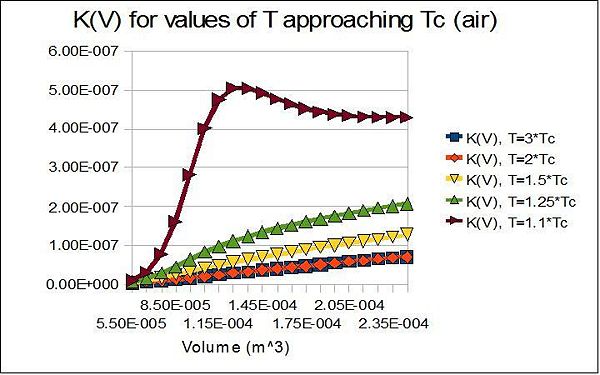
Part 2

We find the critical points for Volume and Temperature when

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac {\partial P} {\partial V} = 0} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac {\partial^2 P} {\partial V^2} =0 }

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\partial P \over \partial V} = -{ Nk_BT \over \left( {V-Nb} \right)^2 } + { 2N^2a \over V^3}=0}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\partial^2 P \over \partial V^2} = { Nk_BT \over \left( {V-Nb} \right)^3 } - { 2N^2a \over V^4}=0}

Using the two equations to solve for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_c} we find that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_c=3 N b}

Plugging Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_c} into the first equation it is found that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k_B T_c={8 a \over 27 b}}

These two critical points are all that is necessary to solve for in order to find the isothermal compressibility.

Part 3

In this part of the homework one is to find that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \kappa \left(t\right)} is proportional to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(T - T_c\right)^{-\gamma}} . First remember the identities for the critical volume and temperature:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_c = 3Nb}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_c = {8a \over 27 k_B b}}

Recall from part 1 that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P = \left({Nk_BT \over V-Nb}\right) - {N^2a \over V^2}} Then taking the partial derivative with respect to V at constant T: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left( {\partial P \over \partial V} \right)_T = -{ Nk_BT \over \left( {V-Nb} \right)^2 } + { 2N^2a \over V^3}}

Here is the best point to evaluate this function at the critical volume and pressure. This changes the function to: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left( {\partial P \over \partial V} \right)_T = -{ Nk_BT \over \left( {V_c-Nb} \right)^2 } + { 2N^2a \over V_c^3}}

Then one can use the identity for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_c} to get:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left( {\partial P \over \partial V} \right)_T =-{ Nk_BT \over \left( {V_c-Nb} \right)^2 } + { 2N^2a \over V_c^3} = -{ Nk_BT \over \left( {3Nb-Nb} \right)^2 } + { 2N^2a \over \left(3Nb\right)^3}}

Then reducing: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -{ Nk_BT \over \left( {3Nb-Nb} \right)^2 } + { 2N^2a \over \left(3Nb\right)^3} = -{ k_BT \over 4Nb^2 } + { 2a \over 27Nb^3} }

At this point we can take Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {k_B \over 4Nb^2} } out of both fractions:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {k_B \over 4Nb^2} \left( T - {8a \over 27k_Bb} \right) }

If one looks at the equation for the critical temperature one can see that one has:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {k_B \over 4Nb^2} \left( T - {8a \over 27k_Bb} \right) = {k_B \over 4Nb^2} \left( T - T_c \right)}

Now one just needs to solve for the compressibility which is the negative reciprocal of our result (as seen in part 1).

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \kappa_T = -\left( {\partial V \over \partial P} \right)_T = {1 \over {k_B \over 4Nb^2} \left( T - T_c \right)} = {4Nb^2 \over k_B} \left( T - T_c \right)^{-1}}

So this means that the critical exponent gamma is 1.