Solution to Set 5: Difference between revisions
(Layout) |
(Formatting) |
||
| Line 4: | Line 4: | ||
==Problem 1== | ==Problem 1== | ||
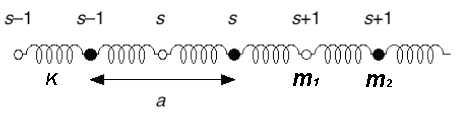
Consider a chain of atoms with alternating masses <math>m_1\;</math> and <math>m_2\;</math>, connected with elastic springs with constant <math>K\;</math>, moving only in the x-direction. | |||
[[Image:chainatoms.jpg]] | |||
Derive the dispersion relation <math>\omega^{\alpha} (k)\;</math> for this chain, with the index <math>\alpha = 1,2\;</math> coresponding to the acoustic and the optical branch, respectively. | |||
==Problem 2== | ==Problem 2== | ||
Determine the speed of sound for this chain. What is the lowest frequency of long-wavelength sound corresponding to the optical branch? | |||
==Problem 3== | ==Problem 3== | ||
Sketch the motion of the atoms corresponding to the edge of the Brillouin zone, both for the optical and the acoustic branch. | |||
==Problem 4== | ==Problem 4== | ||
Determine the Debye temperature for this system, and determine the form of the specific heat <math>c_V (T)</math> in the limits of high and low temperatures. | |||
==Problem 5== | ==Problem 5== | ||
Consider low temperatures (<math> T \ll T_D\;</math>) and determine the wavelength of the most abundant phonons <math>\lambda_{max}</math> (Hint: note the analogy with Wien's Law!) | |||
Revision as of 03:08, 2 March 2009
Let's help each other, considering the importance of this HW, and get started on the solution to this thing
Diatomic harmonic chain
Problem 1
Consider a chain of atoms with alternating masses and , connected with elastic springs with constant , moving only in the x-direction.
Derive the dispersion relation for this chain, with the index coresponding to the acoustic and the optical branch, respectively.
Problem 2
Determine the speed of sound for this chain. What is the lowest frequency of long-wavelength sound corresponding to the optical branch?
Problem 3
Sketch the motion of the atoms corresponding to the edge of the Brillouin zone, both for the optical and the acoustic branch.
Problem 4
Determine the Debye temperature for this system, and determine the form of the specific heat in the limits of high and low temperatures.
Problem 5
Consider low temperatures () and determine the wavelength of the most abundant phonons (Hint: note the analogy with Wien's Law!)