Solution to Set 5

I have no idea what I'm doing - KimberlyWynne 03:11, 2 March 2009 (EST)

Diatomic harmonic chain

Problem 1

Given:

• a chain of atoms
• with alternating masses $m_{1}\;$ and $m_{2}\;$
• connected with elastic springs with constant $K\;$
• moving only in the x-direction

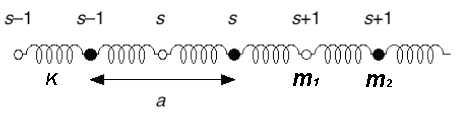
Derive the dispersion relation $\omega ^{\alpha }(k)\;$ for this chain

Index $\alpha =1\;$ for acoustic branch

Potential Energy $U=1,2,3,...n\;$

$U\cong {\frac {1}{2}}k\sum _{n}(U_{n}-U_{n-1})\;$

$\Rightarrow m{\ddot {U}}_{n}=-k[2U_{n}-U_{n-1}-U_{n+1}]=-m\omega U(t)\;$

Eigenvectors of Modes A and B (defined arbitrarily)

$u_{m}(t)=e^{i\omega t}u_{m}\;$

$\Rightarrow -m\omega ^{2}{\ddot {\vec {u}}}_{n}=-k\mathbf {M} {\vec {u}}\;$

Band Matrix

$\mathbf {M} ={\begin{vmatrix}2&1&0&0\\1&2&1&0\\0&1&2&1\\0&0&1&2\end{vmatrix}}$

Running waves through a solid

$u_{m}(t)=e^{ik(na)-\omega t}=e^{ikR_{n}}\;$

where

$u_{m}\rightarrow u_{n}e^{ik(na)}\;$

$R_{n}\;$ = distance on some coordinate system

$\Rightarrow -m\omega ^{2}{\vec {u}}=-k[2-e^{ik\alpha }-e^{-ik\alpha }]\;$

Derive and get:

$\Rightarrow \omega (k)=2{\sqrt {\frac {k}{m}}}|sin(ka)|$

Index$\alpha =2\;$ for optical branch

$u_{m}(t)=e^{ik(na)-\omega t}=e^{ikR_{n}}\;$

$u(R_{n})\equiv e^{ikR_{n}}=cos(ka)\;$

$\Rightarrow -m\omega ^{2}e^{ikna}=-k[2e^{ik(na)}-e^{ik(n+1)a}-e^{ik(n-1)a}]\;$

$\Rightarrow m\omega ^{2}=k[2-(e^{ika}+e^{-ika})]\;$

$\Rightarrow \omega ^{2}={\frac {2k}{m}}[1-cos(ka)]\;$

$\Rightarrow \omega ^{2}={\frac {\Delta k}{m}}{\frac {1}{2}}[1-cos(ka)]\;$

$\Rightarrow \omega ^{2}={\frac {\Delta k}{m}}sin^{2}({\frac {ka}{2}})\;$

$\Rightarrow \omega (k)=2{\sqrt {\frac {k}{m}}}|sin({\frac {ka}{2}})|\;$

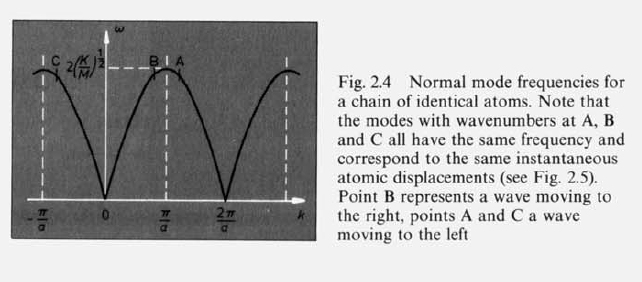
Problem 2

Determine the speed of sound for this chain. What is the lowest frequency of long-wavelength sound corresponding to the optical branch?

From my lecture notes: $\omega _{\alpha }(k)\approx C_{\alpha }k\;$

where $C_{\alpha }$ = speed of sound

Problem 3

Sketch the motion of the atoms corresponding to the edge of the Brillouin zone, both for the optical and the acoustic branch.

Problem 4

Determine the Debye temperature for this system, and determine the form of the specific heat $c_{V}(T)$ in the limits of high and low temperatures.

Problem 5

Consider low temperatures ($T\ll T_{D}\;$) and determine the wavelength of the most abundant phonons $\lambda _{max}$ (Hint: note the analogy with Wien's Law!)