Solution to Set 5: Difference between revisions

From PhyWiki
Jump to navigation Jump to search
Line 18: Line 18:


'''Derive the dispersion relation <math>\omega^{\alpha} (k)\;</math> for this chain'''
'''Derive the dispersion relation <math>\omega^{\alpha} (k)\;</math> for this chain'''
=== Index <math>\alpha = 1\;</math> for acoustic branch ===
Potential Energy <math>U = 1, 2, 3, ... n \;</math>
<math>U \cong \frac{1}{2} k \sum_{n} (U_n - U_{n-1}) \;</math>
<math>\Rightarrow m \ddot{U}_n = - k [2U_n - U_{n-1} - U_{n+1}] = -m \omega U(t) \;</math>
Eigenvectors of Modes A and B (defined arbitrarily)
<math>u_m(t)=e^{i\omega t} u_m \;</math>
<math>\Rightarrow -m \omega ^2 \ddot{\vec{u}}_n = - k \mathbf{M} \vec{u} \;</math>
Band Matrix
<math>
\mathbf{M} = \begin{vmatrix}
2 & 1 & 0 & 0\\
1 & 2 & 1 & 0\\
0 & 1 & 2 & 1\\
0 & 0 & 1 & 2
\end{vmatrix}
</math>
Running waves through a solid
<math>u_m (t) = e^{ik(na)- \omega t} = e^{i k R_n} \;</math>
where
<math>u_m \rightarrow  u_n e^{ik(na)} \;</math>
<math>R_n \;</math> = distance on some coordinate system
<math>\Rightarrow -m \omega ^2 \vec{u} = - k [2 - e^{ik \alpha} - e^{-ik \alpha}] \;</math>
Derive and get:
<math>\Rightarrow \omega (k) = 2 \sqrt{ \frac{k}{m} } |sin(ka)|</math>
=== '''Index<math>\alpha = 2\;</math> for optical branch''' ===
<math>u_m (t) = e^{ik(na)- \omega t} = e^{i k R_n} \;</math>
<math>u(R_n) \equiv e^{i k R_n} = cos (k a) \;</math>
<math>\Rightarrow - m \omega^2 e^{ikna} = -k [2e^{ik(na)} - e^{ik(n+1)a} - e^{ik(n-1)a}] \;</math>
<math>\Rightarrow m \omega^2 = k [2 - (e^{ika}  + e^{-ika})] \;</math>
<math>\Rightarrow \omega^2 = \frac{2k}{m} [1 - cos(ka)] \;</math>
<math>\Rightarrow \omega^2 = \frac{\Delta k}{m} \frac{1}{2} [1 - cos(ka)] \;</math>
<math>\Rightarrow \omega^2 = \frac{\Delta k}{m} sin^{2}(\frac{ka}{2}) \;</math>
<math>\Rightarrow \omega (k) = 2 \sqrt{ \frac{k}{m} } |sin(\frac{ka}{2})| \;</math>


[[Image:Dispersionrelation.jpg]]
[[Image:Dispersionrelation.jpg]]

Revision as of 17:09, 2 March 2009

I have no idea what I'm doing - KimberlyWynne 03:11, 2 March 2009 (EST)

Diatomic harmonic chain

Problem 1

I found this site somewhat helpful and explanatory:

http://newton.ex.ac.uk/teaching/resources/rjh/phy2009/PHY2009handout13.pdf


Given:

  • a chain of atoms
  • with alternating masses Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m_1\;} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m_2\;}
  • connected with elastic springs with constant Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle K\;}
  • moving only in the x-direction

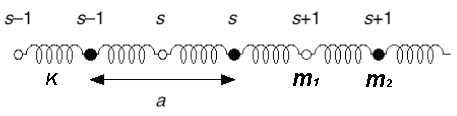
Chainatoms.jpg

Derive the dispersion relation Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega^{\alpha} (k)\;} for this chain

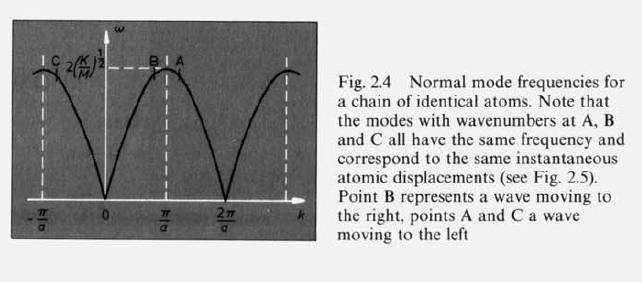
Dispersionrelation.jpg

Problem 2

Determine the speed of sound for this chain. What is the lowest frequency of long-wavelength sound corresponding to the optical branch?

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega _{\alpha }(k)\approx C_{\alpha } k \;}

where

  • Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega_{\alpha } \;} = frequency
  • Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C_{\alpha } \;} = speed of sound
  • Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k \;} = ???

Problem 3

Sketch the motion of the atoms corresponding to the edge of the Brillouin zone, both for the optical and the acoustic branch.

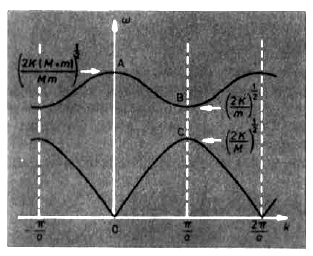
Dispersionbranches.jpg

  • Acoustic Branch: lower branch
  • Optical Branch: upper branch, as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k \rightarrow 0 } on this branch the vibrations of the 2 types of atom are in antiphase and the resulting charge oscillation in an ionic craystal give a strong coupling to electromagnetic waves at the frequency of point A.

Problem 4

Determine the Debye temperature for this system, and determine the form of the specific heat Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C_V (T)} in the limits of high and low temperatures.

Debye Temperature Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_D \;}

The Debye temperature, aka the effective sonic velocity, is a measure of the hardness of the crystal

From our class lectures:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k_B T_D = \hbar \omega_D = \hbar c k_D \;}

From Wikipedia:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_D\ \stackrel{\mathrm{def}}{=}\ {hc_sR\over2Lk} = {hc_s\over2Lk}\sqrt[3]{6N\over\pi} = {hc_s\over2k}\sqrt[3]{{6\over\pi}{N\over V}}}

Specific Heat Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C_V \;}

Low Temperature Limit

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{C_V}{Nk} \sim {12\pi^4\over5} \left({T\over T_D}\right)^3}

High Temperature Limit

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_{high} >> \frac{\hbar\omega}{k_B} \;}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\hbar\omega}{k_B T} << 1 \;}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e^{\frac{\hbar\omega}{k_B T}} \approx 1 + \frac{\hbar\omega}{k_B T} + (\frac{\hbar\omega}{k_B T})^2 \;}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{C_V}{Nk} \sim 3\, }

Net Result (Classical Limit)

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C_V \approx k_B \;}

Problem 5

Consider low temperatures (Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T \ll T_D\;} ) and determine the wavelength of the most abundant phonons Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda_{max}}

Given:

  • Bose-Einstein Distribution Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(E)=\frac{1}{e^{E / k_B T}-1} \;}
    • Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(E) \;} = probability that a particle will have energy E
    • Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k_B \;} = Boltzmann constant
    • Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T \;} = Temperature
  • Planck's Radiation Formula Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E = \frac{h \omega}{e^{h \omega / k_B T} - 1} \;}
    • Density by frequency: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho (\omega) = \frac{dn_s}{d\omega} = \frac{8 \pi}{c^3} \omega^{2} \;}
    • Density by wavelength: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho (\lambda) = \frac{dn_s}{d\lambda} = \frac{8 \pi}{\lambda^{4}} \;}
  • Wien's law Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda_{\mathrm{max}} = \frac{b}{T} \;}
    • Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda_max \;} is the peak wavelength in meters,
    • Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T \;} = temperature of the blackbody in Kelvin
    • Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b \;} = Wien's displacement constant
Retrieved from "http://wiki.physics.fsu.edu/index.php?title=Solution_to_Set_5&oldid=2586"