PHZ3400 Midterm Two Solution: Difference between revisions
HollyBrown (talk | contribs) |
HollyBrown (talk | contribs) |
||
| Line 8: | Line 8: | ||
<math>Z = \sum_{n}^{\infty}\varepsilon^{-\beta E_n}</math> where n = the number of particles. | <math>Z = \sum_{n}^{\infty}\varepsilon^{-\beta E_n}</math> where n = the number of particles. | ||
However, symmetry breaking, including phase transitions, cannot occur for any finite system[1]. Thus systems must be sufficiently large, <math> n\rightarrow \infty</math>, in order to reach the thermodynamic limit and for symmetry breaking occur. | However, symmetry breaking, including phase transitions, cannot occur for any finite system[1]. Thus systems must be sufficiently large, <math> n\rightarrow \infty</math>, in order to reach the thermodynamic limit and for spontaneous symmetry breaking to occur. | ||
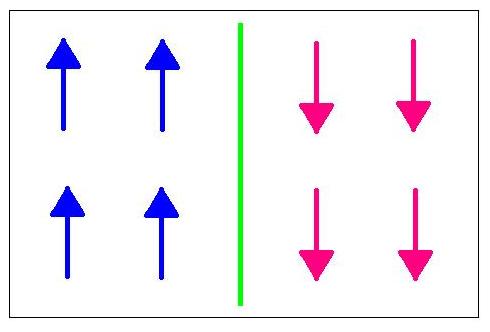
Suppose we start in a system where all of the spins are up and we would like to make them spin down. This can be done by applying a domain wall to the system. | |||
[[Image:DomainWall.jpeg]] | |||
Revision as of 17:20, 15 April 2009
PHZ 3400 – Midterm Two Exam (with solutions) – April 10, 2009
Problem 1
Explain the concept of the "Thermodynamic Limit", and present the corresponding domain wall argument (derivation of a formula) to estimate the relaxation time as a function of system size, at T < Tc.
The partition function which applies in this case is where n = the number of particles.
However, symmetry breaking, including phase transitions, cannot occur for any finite system[1]. Thus systems must be sufficiently large, , in order to reach the thermodynamic limit and for spontaneous symmetry breaking to occur.
Suppose we start in a system where all of the spins are up and we would like to make them spin down. This can be done by applying a domain wall to the system.
[1] [http://prola.aps.org/abstract/PR/v87/i3/p404_1 C. N. Yang and T. D. Lee, Statistical Theory of Equations of State and Phase Transitions. I. Theory of Condensation Phys. Rev. 87, 404 - 409 (1952)]
Problem 2
Sketch the magnetization of a ferromagnet as a function of temperature T, for (A) Zero external magnetic field and (B) Finite external magnetic field. How is the behavior around the Curie Temperature (Tc) affected by the field?