Inflatory Universe and phase transitions of early matter: Difference between revisions
RonaldFrey (talk | contribs) No edit summary |
RonaldFrey (talk | contribs) (slowing inflation) |
||
| Line 5: | Line 5: | ||
== The Inflation Field == | |||
The driving force of this exponential expansion is termed the "inflation field", for lack of a concise term. Let us discuss a simple example. | The driving force of this exponential expansion is termed the "inflation field", for lack of a concise term. Let us discuss a simple example. | ||
| Line 20: | Line 22: | ||
It becomes apparent that this model requires the density to remain constant as the volume increases, requiring the addition of more matter. The decay of the "inflation field" into a lower energy state is thought to be responsible for keeping the density constant by providing matter and radiation. Let us go one step more and convince ourselves that we have not committed a regrettable act and no violation of energy has occurred. The kinetic energy may be defined as <math>\Delta \text{KE}=\int F \, dR=\frac{4 }{3}G\left(m*\pi *R^2*\rho \right)</math>. Notice how the kinetic energy is exactly opposite the potential energy as defined previously. The total energy remains zero since <math>\Delta \text{E}=\Delta \text{KE}+\Delta \text{V}=\frac{4 }{3}G\left(m*\pi *R^2*\rho \right)+-\frac{4 }{3}G\left(m*\pi *R^2*\rho \right)=0</math>. The increase in potential is exactly matched by an increase in kinetic. Matter and energy is not being created from nothing, conservation laws are preserved. | It becomes apparent that this model requires the density to remain constant as the volume increases, requiring the addition of more matter. The decay of the "inflation field" into a lower energy state is thought to be responsible for keeping the density constant by providing matter and radiation. Let us go one step more and convince ourselves that we have not committed a regrettable act and no violation of energy has occurred. The kinetic energy may be defined as <math>\Delta \text{KE}=\int F \, dR=\frac{4 }{3}G\left(m*\pi *R^2*\rho \right)</math>. Notice how the kinetic energy is exactly opposite the potential energy as defined previously. The total energy remains zero since <math>\Delta \text{E}=\Delta \text{KE}+\Delta \text{V}=\frac{4 }{3}G\left(m*\pi *R^2*\rho \right)+-\frac{4 }{3}G\left(m*\pi *R^2*\rho \right)=0</math>. The increase in potential is exactly matched by an increase in kinetic. Matter and energy is not being created from nothing, conservation laws are preserved. | ||
== Slowing Inflation == | |||
At this point the universe is expanding at such a rate, particles are fleeing exponentially rapidly from nearest neighbors. Any organized structures would be impossible to form and our universe would become a very empty place. The weak interaction between quarks would never be able to bind into atoms against the inflation field. A delicate balance between inflation and interaction forces must occur. For this to happen, inflation must slow. At this point, a transition from the inflation field occurs. | |||
Revision as of 10:32, 22 April 2009
Inflation Theory
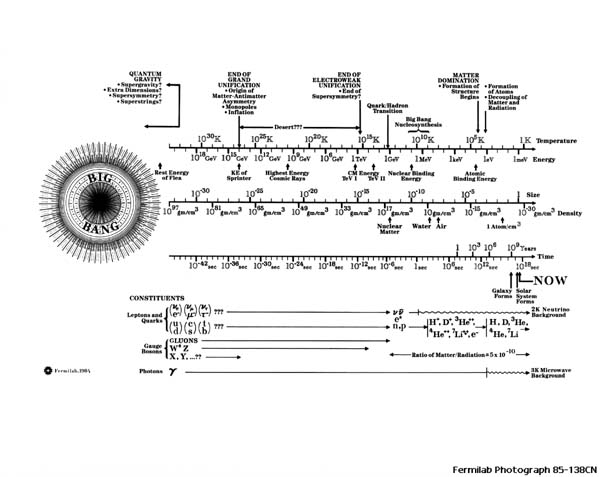
At a point defined as ~Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 10^{-35}} seconds after the critical beginning, a brief period of exponential expansion known as inflation occurred. This inflation lasted until ~Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 10^{-32}} . Before inflation, the size of the universe can be approximated as less than a single proton. After Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 10^{-33}} seconds, the universe has expanded to a size of roughly 10 centimeters. This should be alarming as the rate of expansion exceeds the velocity of light, our maximum allowed speed. For comparative purposes, light takes Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 3*10^{-10}} seconds to travel 1 centimeter. The illusion of expanding away from itself faster than the speed of light is corrected for by understanding that no objects are moving faster than light, spacetime itself is expanding at this exceedingly high rate.
The Inflation Field
The driving force of this exponential expansion is termed the "inflation field", for lack of a concise term. Let us discuss a simple example.
We will create a point at the center of the universe, any point will do since any point can be argued the center. Now we consider a sphere of radius R, containing mass M. On the outer edge of this sphere is a test mass m. Now we apply Newton's law of gravitation to see the behavior of our system. Our gravitational potential is a function of the conditions we have set and the gravitational constant G, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V(R)=-\frac{\text{GmM}}{R}} . Applying a derivative, we calculate the force on our test mass to be Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F=-\frac{\text{dV}}{\text{dR}}=-\frac{\text{GmM}}{R^2}} . We will take this one step further defining the mass M of our system. We know the volume of the sphere to be Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V=\frac{4 \pi R^3}{3}} and mass is simply the product of volume and density. Therefore, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle M=\frac{4}{3} \pi R^3 \rho } . Substituting back into the equation for gravitational force, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F=-\frac{\text{dV}}{\text{dR}}=-G(4/3)m\pi R^2\rho } . No surprises, we have a test mass m and gravity pulls it attractively with a force proportional to the mass density and square of the distance. The negative sign signifies an attractive force.
We have considered the case of an expanding universe with a constant mass M. Now let us consider the case in which the density Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho}
is constant. Again we use Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V(R)=-\frac{\text{GmM}}{R}}
. This time we will substitute the mass M for our density Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V(R)=-\frac{4 }{3}G\left(m*\pi *R^2*\rho \right)}
. We find the force on the test mass to be Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F=-\frac{\text{dV}}{\text{dR}}=2G(m*\rho (4/3)\pi *R)}
. The positive sign indicates a repulsive force! In this model, particles are pushed away, allowing the universe to inflate. Upon more careful inspection, notice the only variable parameter is distance R, which increases the force as R increases. This accounts for the exponential rate of expansion during inflation.
It becomes apparent that this model requires the density to remain constant as the volume increases, requiring the addition of more matter. The decay of the "inflation field" into a lower energy state is thought to be responsible for keeping the density constant by providing matter and radiation. Let us go one step more and convince ourselves that we have not committed a regrettable act and no violation of energy has occurred. The kinetic energy may be defined as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta \text{KE}=\int F \, dR=\frac{4 }{3}G\left(m*\pi *R^2*\rho \right)}
. Notice how the kinetic energy is exactly opposite the potential energy as defined previously. The total energy remains zero since Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta \text{E}=\Delta \text{KE}+\Delta \text{V}=\frac{4 }{3}G\left(m*\pi *R^2*\rho \right)+-\frac{4 }{3}G\left(m*\pi *R^2*\rho \right)=0}
. The increase in potential is exactly matched by an increase in kinetic. Matter and energy is not being created from nothing, conservation laws are preserved.
Slowing Inflation
At this point the universe is expanding at such a rate, particles are fleeing exponentially rapidly from nearest neighbors. Any organized structures would be impossible to form and our universe would become a very empty place. The weak interaction between quarks would never be able to bind into atoms against the inflation field. A delicate balance between inflation and interaction forces must occur. For this to happen, inflation must slow. At this point, a transition from the inflation field occurs.