Phy5645: Difference between revisions
LaurelWinter (talk | contribs) |
LaurelWinter (talk | contribs) |
||
| Line 1,499: | Line 1,499: | ||
===Free particle in spherical coordinates=== | ===Free particle in spherical coordinates=== | ||
A free particle is a specific case when <math>V_0=0\!</math> of the motion in a uniform potential <math>V(r)=V_0\!</math>. So it's more useful to consider a particle moving in a uniform potential. The Schrodinger equation for the radial part of the wave function is: | A free particle is a specific case when <math>V_0=0\!</math> of the motion in a uniform potential <math>V(r)=V_0\!</math>. So it's more useful to consider a particle moving in a uniform potential. The Schrodinger equation for the radial part of the wave function is: | ||
:<math>(-\frac{2m}{\hbar^2}\frac{\partial^2}{\partial r^2}+\frac{2m}{\hbar^2}\frac{l(l+1)}{r^2}+V_0)u_l(r)=Eu_l(r)</math> | |||
:<math>\left(-\frac{2m}{\hbar^2}\frac{\partial^2}{\partial r^2}+\frac{2m}{\hbar^2}\frac{l(l+1)}{r^2}+V_0\right)u_l(r)=Eu_l(r)</math> | |||
let <math>k^2=\frac{2m}{\hbar^2}|E-V|</math>. Rearranging the equation gives | let <math>k^2=\frac{2m}{\hbar^2}|E-V|</math>. Rearranging the equation gives | ||
:<math>(-\frac{\partial^2}{\partial r^2}+\frac{l(l+1)}{r^2}-k^2)u_l(r)=0</math> | :<math>\left(-\frac{\partial^2}{\partial r^2}+\frac{l(l+1)}{r^2}-k^2\right)u_l(r)=0</math> | ||
Letting <math>\rho=kr\!</math> gives the equation: | Letting <math>\rho=kr\!</math> gives the equation: | ||
:<math>(-\frac{\partial^2}{\partial\rho^2}+\frac{l(l+1)}{\rho^2})u_l(\rho)=u_l(\rho)=d_ld_l^+u_l(\rho)</math> | :<math>\left(-\frac{\partial^2}{\partial\rho^2}+\frac{l(l+1)}{\rho^2}\right)u_l(\rho)=u_l(\rho)=d_ld_l^+u_l(\rho)</math> | ||
where <math>d_l\!</math> and <math>d_l^{\dagger}\!</math> become the raising and lowering operators: | where <math>d_l\!</math> and <math>d_l^{\dagger}\!</math> become the raising and lowering operators: | ||
:<math>d_l=\frac{\partial}{\partial\rho}+\frac{l(l+1)}{\rho}, d_l^\dagger=-\frac{\partial}{\partial\rho}+\frac{l(l+1)}{\rho}</math> | :<math>d_l=\frac{\partial}{\partial\rho}+\frac{l(l+1)}{\rho}, d_l^\dagger=-\frac{\partial}{\partial\rho}+\frac{l(l+1)}{\rho}</math> | ||
| Line 1,511: | Line 1,512: | ||
:<math>u_0(\rho)=A\sin(\rho)+B\cos(\rho)\!</math> | :<math>u_0(\rho)=A\sin(\rho)+B\cos(\rho)\!</math> | ||
Now applying the raising operator to the ground state | Now applying the raising operator to the ground state | ||
:<math>d_0^\dagger u_0(\rho)=(-\frac{\partial}{\partial\rho}+\frac{l+1}{\rho})u_0(\rho)=c_0 u_1(\rho)</math> | :<math>d_0^\dagger u_0(\rho)=\left(-\frac{\partial}{\partial\rho}+\frac{l+1}{\rho}\right)u_0(\rho)=c_0 u_1(\rho)</math> | ||
===Spherical well=== | ===Spherical well=== | ||
Dividing the potential into two regions, <math>0<r<a\!</math> and <math>r>a\!</math>, | Dividing the potential into two regions, <math>0<r<a\!</math> and <math>r>a\!</math>, | ||
Revision as of 16:20, 25 October 2009
Welcome to the Quantum Mechanics A PHY5645 Fall2008/2009
This is the first semester of a two-semester graduate level sequence, the second being PHY5646 Quantum B. Its goal is to explain the concepts and mathematical methods of Quantum Mechanics, and to prepare a student to solve quantum mechanics problems arising in different physical applications. The emphasis of the courses is equally on conceptual grasp of the subject as well as on problem solving. This sequence of courses builds the foundation for more advanced courses and graduate research in experimental or theoretical physics.
The key component of the course is the collaborative student contribution to the course Wiki-textbook. Each team of students is responsible for BOTH writing the assigned chapter AND editing chapters of others.
Team assignments: Fall 2009 student teams
Fall 2009 Midterm is October 15
Outline of the course:
Physical Basis of Quantum Mechanics
Basic concepts and theory of motion in QM
In Quantum Mechanics, all of the information of the system of interest is contained in a wavefunction , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Psi\,\!} . Physical properties of the system such as position, linear and angular momentum, energy, etc. can be represented via linear operators, called observables. These observables are a complete set of commuting Hermitian operators, which means that the common eigenstates (in the case of quantum mechanics, the wavefunctions) of these Hermitian operators form an orthonormal basis. Through these mathematical observables, a set of corresponding physical values can be calculated.
In order to clarify the paragraph above, consider an analogous example: Suppose that the system is a book, and we characterize this book by taking measurements of the dimensions of this book and its mass (The volume and mass are enough to characterize this system). A ruler is used to measure the dimensions of the book, and this ruler is the observable operator. The length, width, and height (values) from the measurements are the physical values corresponding to that operator (ruler). For measuring the weight of the book, a balance is used as the operator. The measured mass of the book is the physical value for the corresponding observable. The two observable operators (the ruler and the mass scale) have to commute with each other, otherwise the system can not be characterized at the same time, and the two observables can not be measured with infinite precision.
In quantum mechanics, there are some measurements that cannot be done at the same time. For example, suppose we want to measure the position of an electron. What we would do is send a signal (a gamma ray, for example), which would strike the electron and return to our detectors. We have, then, the position of the electron. But as the photon strikes the electron, the electron gains additional momentum, and our simultaneous momentum measurement can not be precise. Therefore both momentum and position cannot be measured at the same time. These measurement are often called "incompatible observables." This is explained in the Heisenberg uncertainty principle and implies, mathematically, that the two operators do not commute.
This concept contrasts with classical mechanics, where the two observables that do not commute with each other can still be measured with infinite precision. This is because of the difference in dimension of the object: macroscopic (classical mechanics) and microscopic scale (quantum mechanics). However, the prediction of quantum mechanics must be equivalent to that of the classical mechanics when the energy is very large (classical region). This is known as the Correspondence Principle, formally expressed by Bohr in 1923.
We can explain this principle by the following: In quantum mechanics, particles cannot have arbitrary values of energy, only certain discrete values of energy. There are quantum numbers corresponding to specific values of energy and states of the particle. As the energy gets larger, the spacing between these discrete values becomes relatively small and we can regard the energy levels as a continuum. The region where the energy can be treated as a continuum is what is called the classical region.
UV Catastrophe (Black Body Radiation)
To begin an overview of the evolution of Quantum Mechanics, one must first examine its birthplace, i.e. the black body radiation problem. It is simple to understand that emission of radiation from an object occurs for all temperatures greater then absolute zero. As the temperature of the object rises the energy concentration of the emitted radiation (the spectral distribution) shifts away from the long wavelength, i.e. infrared regions, to the shorter wavelength regions, including the visible spectrum and finally the UV and X-ray regions. Coherently, the total power radiated increases with temperature.
Imagine a perfect absorber cavity (i.e. it absorbs all radiation at all wavelengths, so that its spectral radiance only depends on temperature). From Kirchoff's law it follows that such a body would not only be a perfect absorber, but also a perfect emitter of radiation. This emission is called the black body radiation. Lord Rayleigh (John William Strutt) and Sir James Jeans applied classical physics and assumed that the radiation in this perfect absorber could be represented by standing waves. Although the Rayleigh-Jeans result does approach the experimentally recorded values for large values of wavelength, the trend line vastly differs as the wavelength is allowed to tend towards zero. The result predicts that the spectral intensity will increase quadratically with increasing frequency, and would diverge to infinite energy as the wavelength went to zero. For short wavelengths, this became known as the so called "Ultraviolet Catastrophe." This black body radiation experiment shows an important failure of classical mechanics. The Rayleigh-Jeans law is as follows:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho_\lambda(T) = \frac{2 c k T}{\lambda^4}}
where c is the speed of light, k is Boltzmann's constant and T is the temperature in kelvins. In 1900, Max Planck offered a successful explanation for black body radiation. He too postulated that the radiation was due to oscillations of the electron, but the difference between his assumption and Rayleigh's was that he argued that the possible energies of an oscillator were not continuous. He proposed that the energy of an oscillator would be proportional to a constant of the frequency.
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E=h\nu=\hbar\omega}
Here E is energy, h is the Planck constant (Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle h=6.626*10^{-34} Joule-seconds \!} ) and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \nu\!} is the frequency of the oscillator. With the concept of energy being discrete in mind, the result is that Planck's calculation avoided the UV catastrophe, and instead the energy approached zero as the frequency tends to infinity increased. Planck's law of black body radiation is as follows:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho_\lambda(T) = \frac{2 c^2}{\lambda^5}~\frac{h}{e^\frac{hc}{\lambda kT}-1}}
Before leaving the subject of Black Body Radiation it is important to look at one fundamental realization that has come out of the mathematics. In 1964, A. Penzias and R. Wilson discovered a radio signal of suspected cosmic origin, with an intensity corresponding to approximately 3 K. Upon application of Planck's theorem for said radiation, it soon became evident that the spectrum seen corresponded to that of a black body at 3 K, and since this radiation was incident on Earth evenly from all directions, space itself was deemed to be the emitting black body. This cosmic background radiation gave credence to the Big Bang theory, and upon analysis of an expanding system, allowed for proof that Planck's theorem holds for black bodies of changing size. The results of this particular proof even allow for a fair estimation into the rate of expansion of the universe since the time the black body radiation was emitted.
Homework Problem :[1]
Photoelectric Effect
Another contributing factor to the emergence of the theory of Quantum Mechanics came with the realization of the dual nature of light through explanation of the photoelectric effect.
Consider a system composed of light hitting a metal plate. From experimental observations, first observed by Hertz in 1887, and later by Hallwachs, Stoletov, and Lenard in 1900, a current can be measured when light is incident on the metal plate. During this period, the classical point of view was that an electron was bound inside of an atom, and an excitation energy was needed in order to release it from the atom. This energy could be brought forth in the form of light. The classical point of view also included the idea that the energy of the light was proportional to its intensity. Therefore, if enough energy (light) is absorbed by the electron, the electron would eventually be released. However, this was not the case. Several odd results came from these studies. First it was noted that, while the current did appear to be proportional to the intensity of the incident light, there were certain minimum frequencies of light below which no current could be produced, regardless of the intensity of the incident beam. Also, the stopping potential of the emitted electrons appeared to depend upon the frequency of the radiation, and not the intensity at all. Finally, the emission appeared to take place instantaneously for any intensity so long as the minimum frequency condition was satisfied.
In 1905, Einstein began offering possible explanations for the odd observations made regarding the photoelectric effect. Einstein realized that the classical view of light as a wave was not entirely true, that light must also behave like a particle. This allowed him to postulate that the energy of the incident radiation was not continuous, but was rather composed of quantized packets, proportional to the frequency of the wavelength of incident light. These corpuscles could then be seen to be completely absorbed by an atom, rather then spreading out over the structure like a wave would, so that the absorption/emission would happen instantly. He commented that since electrons were inherently bound to the atom, a certain minimum energy would be required to remove them, and thus if a corpuscle did not have enough energy, i.e. its frequency was too low, the atom would merely absorb and release it, rather then kicking out an electron as well. From this result, Millikan was able to confirm Einstein's theory a few years later by showing that the stopping potential did indeed depend linearly with respect to the frequency, with an additive term corresponding to the minimum energy required to remove the electron, its work function.
From these results it was clearly evident that light was behaving in a particle-like manner, however the existence of various interference and diffraction experiments still gave evidence for a wave-like nature as well, and thus the dual nature of light was exposed, in stark contrast to classical physics.
Stability of Matter
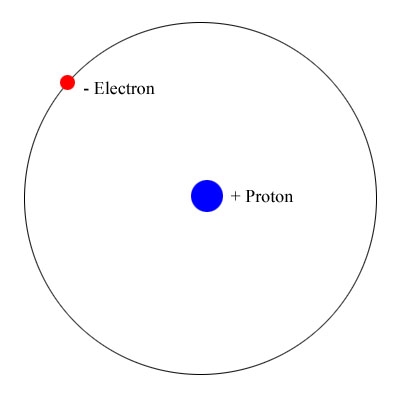
One of the most important problems to inspire the creation of Quantum Mechanics was the model of the Hydrogen Atom. After Thompson discovered the electron, and Rutherford, the nucleus (or Kern, as he called it), the model of the Hydrogen atom was refined to one of the lighter electron of unit negative elementary charge orbiting the larger proton, of unit positive elementary charge. However, it was well known that classical electrodynamics required that charges accelerated by an EM field must radiate, and therefore lose energy. For an electron that moves in circular orbit about the more massive nucleus under the influence of the Coulomb attractive force, here is a simple non-relativistic model of this classical system:
Where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r\,\!} is the orbital radius, and we neglect the motion of the proton by assuming it is much much more massive than the electron.
So the question is: What determines the rate Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho} of this radiation? and how fast is this rate?
The electron in the Bohr's model involves factors of: radius Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r_0\,\!} , angular velocity Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega\,\!} , charge of the particle Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e\,\!} , and the speed of light, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c\,\!} : Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho=\rho(r_0,\omega,e,c)\,\!}
The radius and charge will not enter separately, this is because if the electron is far from the proton, then the result can only depend on the dipole moment, which is .
Therefore the above parameters is now:Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho(er_0, \omega, c) \!}
What are the dimensions of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho\,\!} ?
Essentially, since light is energy, we are looking for how much energy is passed in a given time: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [\rho]=\frac{energy}{time} \!}
Knowing this much already imposes certain constraints on the possible dimensions. By using dimensional analysis, let's construct something with units of energy.
From potential energy for coulombic electrostatic attractions: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle energy=\frac{e^2 }{length} \!}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e} has to be with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r_0} , multiply by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r^2} , and divide Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle length^2} .
The angular velocity is in frequency, so to get the above equations in energy/time, just multiply it with the angular velocity, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle energy=\frac{e^2 }{length}\frac{r^2}{length^2}*\omega }
(Here, it is seen that the acceleration of the electron will increase with decreasing orbital radius. The radiation due to the acceleration a is given by the Larmor Formula: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle energy \sim \frac{e^2r_0^2 }{(c/w)^3} w = \frac{e^2r_0^2 }{c^3}w^4\sim\frac{1}{r_0^4 } \!}
It was known that the hydrogen atom had a certain radius on the order of .5 angstroms. Given this fact it can easily be seen that the electron will rapidly spiral into the nucleus, in the nanosecond scale. Clearly, the model depicts an unstable atom which would result in an unstable universe. A better representation of of an electron in an atom is needed.
Double Slit Experiment
Bullet
Imagine a gun which is spraying bullets randomly toward a wall with two slits in it separated by a distance, d. The slits are about the size of a bullet. A histogram of the bullet's location after it passes through the two slits is plotted. If slit 2 is closed, but the slit 1 is open, then the green peak is observed which is given by the distribution function Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p_1} . Similarly, if the slit 1 is closed, but he slit 2 is open, the pink peak is observed which is given by the distribution function Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p_2} . When both slits are open, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle peak_{12}} (purple) is observed. This agrees with the classical view, where the bullet is the particle and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p_{12}} is simply a sum of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p_1} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p_2} . The bullets do not follow purely linear trajectories because they are allowed to hit the edges of the slits they pass through and be deflected. It is because the bullets can be deflected that the result of this experiment is a probability distribution rather than the bullets going to just the two locations that are along straight line trajectories from the gun through the slits.
The equation describing the probability of the bullet arrival if both of the slit are open is therefore
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p_{12}=p_1+p_2.\!}
Classical Waves
As waves are passed through the double slit, they are diffracted so that the waves emerge from the slit as circular waves, this effect can only occur when the size of the slits is comparable to the wavelength. The intensity of the waves which are proportional to the squares of the height of the wave motion Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H_1^2}
and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H_2^2}
are observed when slit 1 and 2 are closed respectively. These intensities are similar to the histograms for the bullets in the previous demonstration. However, an interference pattern of the intensity (Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H_{12}}
) is observed when both slits are opened. This is due to constructive and destructive interferences of the two waves. The resultant interference is the square of the sum of the two individual wave heights
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H_{12} = (H_{1} +H_{2} )^2\!}
Hot Tungsten Wire (thermal emission of electrons)
A high current is passed through a tungsten wire, resulting in electrons being emitted from the wire which then enter the double slits one at a time, arriving in the same manner as the bullet arrives from the gun. However, after plotting a histogram of the locations where the electron landed, it looks like H_{12} for the double slit wave experiment. This shows that electrons exhibit both the wave and the particle-like character. The probability distribution of the electron's landing on the screen thus exhibits the interference patterns. It is the laws obeyed by these probability "amplitudes" that Quantum Mechanics describes.
[1] R.P. Feynman, R.B. Leighton and M.L.Sands The Feynman Lectures on Physics, vol 3, Addison-Wesley, (1989), Chapter 1.
Schrödinger equation
Imagine a particle constrained to move along a the x-axis, subject to some force Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F(x,t)\!} . Classically, we would investigate this system by applying Newton's second law, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F = ma} . Assuming the force is conservative, it could also be expressed as the partial derivative with respect to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} , and Newton's second law then reads:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{d^2x}{dt^2}=-\frac{\partial V}{\partial x}}
The energy for a particle in this regime is given by the addition of its kinetic and potential energies:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E = T + V = \frac{p^2}{2m} + V}
Now by applying the appropriate initial conditions for our particle, we then have a solution for the trajectory of the particle. As we will see, the above relation is only an approximation to actual physical reality. As we attempt to describe increasingly smaller objects we enter the quantum mechanical regime, where we cannot neglect the particles' wave properties. Allowing Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle{p \rightarrow \frac{\hbar}{i}\frac{d}{dx}}} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle{E \rightarrow i\hbar \frac{d}{dt}}} , we can use the energy equation for a classical particle above to find an equation that describes this wave nature. Thus, we find that the complex amplitude satisfies the Schrodinger equation (below) subject to a (scalar) potential Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V(x,t)} : Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i\hbar\frac{\partial}{\partial t}\psi(x,t)=\left[-\frac{\hbar^2}{2m}\frac{\partial^2}{\partial x^2}+V(x)\right]\psi(x,t) } 1D Schrodinger equation subject to a (scalar) potential 2.0.1
While in 3D:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i\hbar\frac{\partial}{\partial t}\psi(r,t)=\left[-\frac{\hbar^2}{2m}\nabla^2+V(r)\right]\psi(r,t)} 3D Schrodinger equation subject to a (scalar) potential 2.0.2
Given a solution which satisfies the above Schrodinger equation, Quantum Mechanics provides a mathematical description of the laws obeyed by the probability amplitudes associated with quantum motion.
Stationary states
Stationary states are the energy eigenstates of the Hamiltonian operator. These states are called "stationary states" because their eigenvalues Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E} are independent of time.
For a conservative system with a time independent potential, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V(\textbf{r})} , the Schrödinger equation takes the form:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i\hbar\frac{\partial \psi(\textbf{r},t)}{\partial t} = \left[ -\frac{\hbar^2}{2m}\nabla^2 + V(\textbf{r})\right]\psi(\textbf{r},t)}
Since the potential and the Hamiltonian do not depend on time, solutions to this equation can be written as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi(\textbf{r},t)=e^{-iEt/\hbar}\psi(\textbf{r})} . Then the eigenvalue equation Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H\psi(\textbf{r}) = E\psi(\textbf{r})} can be written as:
where is the eigenfunction of the Hamiltonian operator. This equation is known as the time-independent Schrödinger equation.
If time t is fixed, evaluated and integrated over all space, the probability will be equal to one. This is a consequence of the wavefunction being normalized over time.
The probability amplitude, , can be interpreted as probability density. To show that this is true, two conditions must be met. First, the probability amplitude must be positive semi-definite (equal to or greater than zero). This condition is trivial because the magnitude of is always a positive function. Second, the probability amplitude must be conserved. This condition can be shown by proving that if the wavefunction is normalized at some time then it must be normalized for any time :
Does the solution to the Schrodinger Equation conserve the probability, i.e. are we guaranteed that the probability to find the particle somewhere in the space does not change with time? To see that it does, consider
Taking a complex conjugate
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -i\hbar\psi(x,t)\frac{\partial}{\partial t}\psi^*(x,t)=\psi(x,t)\left[-\frac{\hbar^2}{2m}\frac{\partial^2}{\partial x^2}+V(x)\right]\psi^*(x,t)}
and taking the difference of the above equations we finally find
Note that this is in the form of a continuity equation
where
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho(r,t)=\psi^*(r,t) \psi(r,t)\!}
is the probability density
and
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle j(r,t)=\frac{\hbar}{2im}\left[\psi^*(r,t)\nabla \psi(r,t)-\psi^*(r,t)\nabla \psi(r,t)\right]} is the probability current.
Once we know that the densities and currents constructed from the solution of the Schrodinger equation satisfy the continuity equation, it is easy to show that the probability is conserved. To see that note:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial}{\partial t}\int d^3r |\psi(r,t)|^2=-\int d^3r(\nabla\cdot j)=-\oint dA\cdot j =0}
where we used the divergence theorem which relates the volume integrals to surface integrals of a vector field. Since the wavefunction is assumed to vanish outside of the boundary the current vanishes as well. The time independence of the probability to find particle somewhere in space is what we wished to prove.
States, Dirac bra-ket notation
The physical state of a system is represented by a set of probability amplitudes (wave functions), which form a linear vector space. This linear vector space is called the Hilbert Space. Another way to think about the Hilbert space is as an infinite dimensional space of square normalizable functions. This is analogous to 3-dimensional space, where the basis is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left( \hat{i}, \hat{j}, \hat{k}\right)} in a generalized coordinate system. In the Hilbert space, the basis is formed by an infinite set of complex functions. So the basis in a Hilbert space looks like Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left( |\psi_0\rangle, |\psi_1\rangle, |\psi_2\rangle, ... , |\psi_j\rangle, ... \right) } .
A state vector Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi\ } in Hilbert space is denoted in Dirac notation by a “ket” Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle | \psi \rangle} , and its complex conjugate Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi\ } * is denoted by a “bra” Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle\psi |} .
So the basis in a Hilbert space looks like Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left( |\psi_0\rangle, |\psi_1\rangle, |\psi_2\rangle, ... , |\psi_j\rangle, ... \right) } . Therefore, in the space of wavefunctions that belong to the Hilbert space, any wavefunction can be written as a linear combination of the basis function: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle | \phi \rangle = \sum_n c_n|\psi_n\rangle } , where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c_n } denotes a complex number.
In Dirac notation, the scalar product of two state vectors (Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi\ } , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi\ } ) is denoted by a “bra-ket” Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle\phi|\psi\rangle } . In coordinate representation the scalar product is given by:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle\phi|\psi\rangle = \int \phi^*(r,t)\psi(r,t)d^3r }
In Dirac's notation, the eigenfunctions are replaced by eigenkets (or simply kets). In this notation Schrödinger's equation is written as
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i\hbar \frac{\partial}{\partial t}|\psi(t)\rangle=\mathcal{H}|\psi(t)\rangle }
For time independent Hamiltonians, the above equation separates and we can seek the solution of the form of (stationary states)
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\psi(t)\rangle=e^{-iE_n t/\hbar}|\psi_n\rangle} .
The equation for stationary states in the Dirac notation is then
Heisenberg Uncertainty relations
Consider a long string which contains a wave that moves with a fairly well-defined wavelength. The question, "where is the wave" does not seem to make much sense, since it is spread thoughout the length of string. A quick snap of the wrist and the string being held now has a well defined position since the wave's small bump-like wave is noticable. Now the question, "what is the wavelength" does not make sense, since there is no well defined period. Obviously there is a limitation on measuring simultaneously the wavelength and the position. Relating the wavelength to momentum yields the de Broglie equation, which is applicable to any wave phenomenon, including the wave equation:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p=\frac{h}{\lambda}=\frac{2\pi \hbar}{\lambda}}
Now that there is a relation between momentum and position, the uncertainty of the measurement of either momentum or position takes mathematical form in the Heisenberg Uncertainty relation:
where the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta\mathcal{O}} of each operator represents the positive square root of the variance, given generally by:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle(\Delta A)^2\rangle=\langle A^2\rangle-\langle A\rangle^2.}
Although both momentum and position are measurable quantities that will yield precise values when measured, the uncertainty principle states that the deviation in one quantity is directly related to the other quantity. This deviation in the uncertainty principle is the result of identically prepared systems not yielding identical results.
A generalized expression for the uncertainty of any two operators A and B is shown to hold in most any undergraduate text:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta A\Delta B=\frac{1}{2i}\langle [A,B]\rangle.}
And thus, there exists an uncertainty relation between any two observables which do not commute.
More generally the uncertainty principle states that two canonically conjugated variables cannot be determined simultaneously with a precision exceeding the relation:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta A\Delta B = \hbar }
Canonically conjugated variables are those which are related by the Fourier Transform. More specifically, they are variables that when you take the Furrier Transform of a function that is dependent on one, you get a function that depends on the other. For example, if you take the Furrier Transform of a function that depends on position you get a function that depends of momentum, thus position and momentum are canonically conjugated variables. Another example of canonically conjugated variables are energy and time. It is precisely this relationship that leads to the uncertainty principle. The reader has probably noticed that the relation above – i.e. Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta A\Delta B = \hbar } – is not the familiar uncertainty principle we all know, the one where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hbar } is divided by two. It turns out that the above relation is more general; we only get the more familiar version when the wave-packet is Gaussian.
A worked problem showing the uncertainty in the position of different objects over the lifetime of the universe: Uncertainty Relations Problem 1
A problem about how to find kinetic energy of a particle, a nucleon specifically, using the uncertanity principle : Uncertainty Relations Problem 2
Another problem verifying Uncertainty realtion: Verifying the realtion
Motion in one dimension
Overview
Let's consider the motion in 1 direction of a particle in the potential V(x). Supposing that V(x) has finite values when x goes to infinity
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lim_{x \to -\infty}V(x)=V_-, \lim_{x \to +\infty}V(x)=V_+}
and assuming that: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_-<V_+ \!} Schrodinger equation:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [-\frac{\hbar^2}{2m}\frac{d^2}{dx^2}+V(x)]\psi(x)=E\psi(x)}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rightarrow \frac{d^2}{dx^2}\psi(x)+\frac{2m}{\hbar^2}(E-V(x))\psi(x)=0}
From this equation we can discuss some general properties of 1-D motion as follows:
If :
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E-V(x)>0\!} at both and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle +\infty} . Therefore, the solution of Schrodinger equation are trigonometric function (sine or cosine). The wave function is oscillating at both and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle +\infty} . The particle is in unbound state. The energy spectrum is continous. Both oscillating solutions are allowed, the energy level are two-fold degenerate.
If :
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E-V(x)>0\!} at but Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E-V(x)<0} at Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle +\infty} . Therefore, the wave function is oscillating at Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -\infty} but decaying exponentially at Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle +\infty} . The energy spectrum is still continous but no longer degenerate.
If Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E<V_-\!} :
at both Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -\infty} and . Therefore, the wave function decays exponentially at both Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -\infty} and . The particle is in bound state. The energy spectrum is discrete and non-degenerate.
1D bound states
Infinite square well
Let's consider the motion of a particle in an infinite and symmetric square well: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V(x)=+\infty} for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x \ge |L|/2} , otherwise Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V(x)=0\!}
A particle subject to this potential is free everywhere except at the two ends (), where the infinite potential keeps the particle confined to the well. Within the well the Schrodinger equation takes the form:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -\frac{\hbar^2}{2m}\frac{d^2\psi}{dx^2}=E\psi}
or equivalently,
where
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k=\frac{\sqrt{2mE}}{\hbar}}
Writing the Schrodinger equation in this form, we see that our solution are those of the simple harmonic oscillator, i.e. Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi(x) = A \sin (kx) + B \cos (kx)\!} :
Now we impose that the solution must vanish at Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x = \pm L/2} :
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -A\sin(kL/2)+B\cos(kL/2)=0\!}
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A\sin(kL/2)+B\cos(kL/2)=0\!}
Adding the two equations, we get:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2B\cos(kL/2)=0\!}
It follows that either Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B=0\!} or Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \cos(kL/2)=0\!} .
Case 1: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B=0\!} . In this case Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A\ne0\!} , otherwise the wavefunction vanishes every where. Furthermore, it is required that: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sin(kL/2)=0\!}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rightarrow k=2n\pi/L\!} where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n=1,2,3,...\!}
And the wave functions are odd: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi(x)=A\sin(2n\pi x/L)\!}
Case 2: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \cos(kL/2)=0\!} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rightarrow k=(2n+1)\pi/L\!} where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n=0,1,2,...\!}
In this case Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A=0\!} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B\ne0\!} , and the wavefunctions are even: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi(x)=B\cos[(2n+1)\pi x/L]\!}
The two solutions give the eigenenergies Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_n = \frac{\hbar^2}{2m} \left(\frac{\pi n}{L} \right )^2 \!} , where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n = 1,2,3,...\!} These wave numbers are quantized as a result of the boundary conditions, thus making the energy quantized as well. The lowest energy state is the ground state, and it has a non-zero energy, which is due to quantum zero point motion. This ground state is also nodeless, the first excited state has one node, the second excited state has two nodes, and so on. The wavefunctions are also orthogonal.
Parity operator and the symmetry of the wavefunctions
In the above problem, two basic solutions of Schrodinger equation are either odd or even. The general wavefunctions are combinations of odd and even functions. This properties originates from the fact that the potential is symmetric or invariant under the inversion Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x \rightarrow -x} , and so does the Hamiltonian. Therefore, the Hamiltonian commutes with the parity operator Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{P}} (Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{P} \psi(x)=\psi(-x)} ). In this case, the wavefunctions themselves do not need to be odd or even, but they must be some combinations of odd and even functions.
Non-degeneracy of the bound states in 1D
Let's consider a more general property that is the Wronskian for 2 solutions of the 1-D Schrodinger equation must equal to a constant.
Schrodinger equation : Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -\frac{\hbar^2}{2m}\frac{d^2\psi}{dx^2}+V(x)\psi=E\psi}
is a second-order differential equation. Such equation has 2 linearly independent Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi_E^{(1)}} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi_E^{(2)}} for each value of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E\!} :
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -\frac{\hbar^2}{2m}\frac{d^2\psi_E^{(1)}}{dx^2}+V(x)\psi_E^{(1)}=E\psi_E^{(1)}}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -\frac{\hbar^2}{2m}\frac{d^2\psi_E^{(2)}}{dx^2}+V(x)\psi_E^{(2)}=E\psi_E^{(2)}}
By definition in mathematics, the Wronskian of these functions is: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle W=\psi_E^{(1)}\frac{d\psi_E^{(2)}}{dx}-\frac{d\psi_E^{(1)}}{dx}\psi_E^{(2)}}
Multiplying equation (2) by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi_E^{(2)}} , equation (3) by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi_E^{(1)}} , then subtracting one equation from the other, we get:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{d^2\psi_E^{(1)}}{dx^2}\psi_E^{(2)}-\frac{d^2\psi_E^{(2)}}{dx^2}\psi_E^{(1)}=0}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rightarrow \frac{d}{dx}(\frac{d\psi_E^{(1)}}{dx}\psi_E^{(2)}-\frac{d\psi_E^{(2)}}{dx}\psi_E^{(1)})=0}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rightarrow \frac{dW}{dx}=0}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rightarrow W=C}
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C\!} is constant. So, the Wronskian for 2 solutions of the 1-D Schrodinger equation must equal to a constant.
For the bound states, the wave function vanish at infinity, i.e: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi_E^{(1)}(\infty)=\psi_E^{(2)}(\infty)=0}
From (4), (5) and (6), it follows that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle W=0\!} From (4) and (7), we get: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi_E^{(1)}\frac{d\psi_E^{(2)}}{dx}-\frac{d\psi_E^{(1)}}{dx}\psi_E^{(2)}=0}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rightarrow \frac{1}{\psi_E^{(1)}}\frac{d\psi_E^{(1)}}{dx}-\frac{1}{\psi_E^{(2)}}\frac{d\psi_E^{(2)}}{dx}=0}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rightarrow \frac{d}{dx}[ln(\psi_E^{(1)})-ln(\psi_E^{(2)})]=0}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rightarrow ln(\psi_E^{(1)})-ln(\psi_E^{(2)})=constant}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rightarrow \psi_E^{(1)}=constant.\psi_E^{(2)}}
From (8) it follows that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi_E^{(1)}} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi_E^{(2)}} describe the same state. Therefore, the bound states in 1D are non-degenerate.
Scattering states
The scattering states are those not bound, where the energy spectrum is a continuous band. Unlike the bound case, the wave-function does not have to vanish at plus/minus infinity, though a particle can not reflect from infinity often giving a useful boundary condition. At any changes in the potentials, the wave-function must still be continuous and differentiable as for the bound states.
For the delta function potential the derivative of the wave-function is not differential, but has a step. Integrating the schrodinger wave equation from just one side of the step to just the other and then taking the limit as the difference between the integral limits becomes zero.
We have to know wave functions and discrete energy levels Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{E}_{n}}
for bound state problems; but, for scattering states (unbound states) the energy E isn't discrete. We are interested in the wave functions in order to use and determine the transmission and reflection coefficients T and R.
Oscillation theorem
Let us concentrate on the bound states of a set of wavefunctions. Let Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi_1\!} be an eigenstate with energy Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_1\!} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle psi_2\!} an eigenstate with energy Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_2\!} , and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_2>E_1\!} . We also can set boundary conditions, where both Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi_1\!} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi_2\!} vanish at Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_0\!} .This implies that
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -\psi_2\frac{\partial^2 \psi_1}{\partial x^2}+V(x)\psi_2\psi_1=E_1\psi_2\psi_1\!}
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -\psi_1\frac{\partial^2 \psi_2}{\partial x^2}+V(x)\psi_1\psi_2=E_2\psi_1\psi_2\!}
Subtracting the second of these from the first and simplifying, we see that
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial}{\partial x}(-\psi_2\frac{\partial \psi_1}{\partial x}+\psi_1\frac{\partial \psi_2}{\partial x})=(E_1-E_2)\psi_1\psi_2\!}
If we now integrate both sides of this equation from Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_0\!} to any position Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x'\!} and simplify, we see that
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -\psi_2(x')\frac{\partial \psi_1(x')}{\partial x}+\psi_1(x')\frac{\partial \psi_2(x')}{\partial x}=(E_1-E_2)\int_{x_0}^{x'}\psi_1\psi_2dx\!}
The key is to now let Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x'\!} be the first position to the right of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_0\!} where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi_1\!} vanishes.
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -\psi_2(x')\frac{\partial \psi_1(x')}{\partial x}=(E_1-E_2)\int_{x_0}^{x'}\psi_1\psi_2dx\!\!}
Now, if we assume that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi_2\!} does not vanish at or between Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x'\!} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_0\!} , then it is easy to see that the left hand side of the previous equation has a different sign from that of the right hand side, and thus it must be true that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi_2\!} must vanish at least once between Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x'\!} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_0\!} if Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_2>E_1\!} .
Transmission-Reflection, S-matrix
Motion in a periodic potential
An example of a periodic potential is given in Figure 1 which consists of a series of continuous repeating form of potentials. In other words, the potential is translationally symmetric over a certain period (in Figure 1 it is over period of a).
Figure 1.
The Hamiltonian of system under periodic potential commutes with the Translation Operator defined as:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat T_a\psi(x)=\psi(x+a)\!}
This means that there is a simultaneous eigenstate of the Hamiltonian and the Translation Operator. The eigenfunction to the Schrodinger Equation,
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (-\frac{\hbar^2}{2m}\frac{\partial^2}{\partial x^2}+V(x))\psi(x)=E\psi(x)}
has the form of the following,
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi(x)=e^{ikx}u_k(x)\!}
where
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u_k(x+a)=u_k(x)\!}
This result is also known as the Bloch Theorem.
Also, by operating the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat T_a\!} operator on the wavefunction (also known as the Bloch wave), it can be seen that this waveform is also an eigenfunction of the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat T_a\!} operator, as shown in the following,
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \hat T_a\psi(x)&=\hat T_a (e^{ikx}u_k(x))\\ &=(e^{ik(x+a)}u_k(x+a))\\ &=e^{ika}(e^{ikx}u_k(x))\\ &=e^{ika}\psi(x) \end{align}}
Using the same argument, it is clear that,
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (\hat T_a)^n\psi(x)=e^{ikna}\psi(x)}
Also, note that if k is complex, then after multiple operations, the exponential will "blow-up". Thus, k has to be real. Applying the Bloch Theorem in solving Schrodinger Equation with known periodic potential will reveal interesting and important results such as a band gap opening in the Energy vs k spectrum. For materials with weak electron-electron interaction, given the Fermi energy of the system, one can then deduce whether such a system is metallic, semiconducting, or insulating.
Figure 2. Energy band illustration showing the condition for metal, semiconductor, and insulator.
Consider for example the periodic potential and the resulting Schrodinger equation,
Focusing the attention for case when 0 < x < a, the solution to the Schrodinger equation is of the form:
From periodicity,
Thus, the wavefunction from x < 0 (left) and x > 0 (right) can be written as:
When the continuity requirement at x = 0 is also being imposed, the following relation is found:
- (1)
From differentiability and periodicity, the Schrodinger equation can be solved as the following:
where is small, approaching zero. In this case, the term on the right hand side can be taken to be 0. Thus,
where,
Evaluating further, the following condition is found:
- (2)
By simultaneously solving equation (1) and (2), the relationship between q and k is found to be:
- (3)
Homework Problem: [2]
Where q is the energy band of the system, and k is the accessible energy band. By noting that the maximum value of the LHS is < the maximum value of the RHS of the relation above, it is clearly seen that there are some energy level that are not accessible as shown in Figure 3.
Figure 3. Graph of Eq.(3). Wave is representing the LHS function, gray box representing the range of RHS function. Red lines is the forbidden solution, black line is the allowed solution.
As k increases from 0 to , there will be many solutions. Focusing only to two of the allowed solutions, it is seen that as k increases, there will be two solutions (one solution gives increasing q value, the other solution gives decreasing q value). Using the fact that the energy of the system is , the dispersion relation (E vs. k) can be plotted as shown in Figure 4.
Figure 4. Energy vs k showing the existence of band gap for system of an electron under periodic potential.
Thus, in conjunction with Pauli exclusion principle, the single particle banspectrum such as the one we discussed here constitutes a simple description of band insulators and band metals.
Operators, eigenfunctions, symmetry, and time evolution
Commutation relations and simulatneous eigenvalues
Commutators
The commutator of two operators A and B is defined as follows:
When , the operators and commute. Conversely, if , the operators do not commute, and we can think of the commutator between two operators as a quantization of how badly they fail to commute.
Identities:
In addition, if any two operators are Hermetian and their product is Hermetian, then the operators commute because
and
so we have that , which means the commutator is zero.
It should also be noted that any operator will commute with a constant scalar.
Some more complicated commutator identities can be found here http://sites.google.com/site/phy5645fall2008/some-useful-commutator-identites
Also it should be noted that:
However this is only true if:
Compatible observables
An operator which corresponds to some physically measurable property of a system is called an observable. The following is a list of common physical observables and their corresponding operators given in coordinate representation:
All observables are Hermitian. If two Obersvables have simultaneous eigenkets, meaning for two obervables A and B,
Then we have that
Similarly,
So we can see that,
.
The same logic works in reverse. So if two operators, A & B commute, i.e. if , then they have simultaneous eigenkets, and they are said to correspond to compatible observables. Conversely, if , we say that the operators and do not commute and correspond to incompatible observables.
Position and momentum operators
An extremely useful example is the commutation relation of the position operator and momentum . In the position representation, and .
Applying and to an arbitrary state ket we can see that:
The position and momentum operators are incompatible. This provides a fundamental contrast to classical mechanics in which x and p obviously commute.
In three dimensions the canonical commutation relations are:
where the indices stand for x,y, or z components of the 3-vectors.
Connection between classical and quantum mechanics
There is a wonderful connection between Classical mechanics and Quantum Mechanics. The Hamiltonian is a concept in the frame of classical mechanics. In this frame, the Hamiltonian is defined as:
There are two possibilities.
1. If the Lagrangian does not depend explicitly on time the quantity H is conserved.
2. If the Potential and the constraints of the system are time independent, then H is conserved and H is the energy of the system.
It is clear from the above equation that:
This pair of the equations is called Hamilton's equations of motions. The following object
is called Poisson Bracket, and it has interesting properties. To see, let's calculate commutation relationships between coordinates and momenta.
This relations clearly shows how close are the quantum commutators with classical world. If we perform the following identification:
Then we get quantum commutators. This identifications is called canonical quantization. As a final an important remark, the fact that we have classical commutators doesn't mean that we will have Heisenberg uncertainty relation for conjugate classical variables. This is because in classical mechanics the object of study are points (or body as a collection of points). In quantum mechanics we object of study is the state of a particle or system of particles - which describes the probability of finding a particle, and not it's exact, point-like, location of momentum.
Hamiltonian
In Quantum Mechanics an important property is the commutation of a given operator (let's say ) and the Hamiltonian . If commutes with , then the eigenfunctions of can always be chosen to be simultaneous eigenfunctions of . If commutes with the Hamiltonian and does not explicitly depend on time, then is a constant of motion.
Commutators & symmetry
We can define an operator called the parity operator, which does the following:
The parity operator commutes with the Hamiltonian if the potential is symmetric, . Since the two commute, the eigenfunctions of the Hamiltonian can be chosen to be eigenfunctions of the parity operator. This means that if the potential is symmetric, the solutions can be chosen to have definite parity (even and odd functions).
Generalized Heisenberg uncertainty relation
If two opperators are Hermitian and
then
Proof:
First recall and note that is Hermitian if is.
Let be a real scalar and define as such:
- .
So is the norm squared of some arbitrary state vector after operating on it. Hence by the positive semidefinite property of the norm:
Proceeding to calculate this norm squared:
Notice that is a real valued ( expectation values of Hermitian operators are always real ) quadratic in real which is always greater than or equal to zero. This implies that there are no real solutions for or there is exactly 1. This can be seen by attempting to solve for by using the "quadratic formula" :
Now we exploit our insight about the number of real roots and see that the discriminant, the term under the square root, must be either 0 ( yielding 1 real solution for ) or negative ( yielding 0 real solutions ). Stated more succinctly:
which immediately implies what was to be proved.
Heisenberg and interaction picture: Equations of motion for operators
There are several ways to mathematically approach the change of a quantum mechanical system with time. The Schrodinger picture considers wave functions which change with time while the Heisenberg picture places the time dependence on the operators and deals with wave functions that do not change in time. The interaction picture, also known as the Dirac picture, is somewhere between the other two, placing time dependence on both operators and wave functions. The two "pictures" correspond, theoretically, to the time evolution of two different things. Mathematically, all methods should produce the same result.
Definition of the Heisenberg Picture
The time evolution operator is at the heart of the "evolution" of a state, and is the same in each picture. The evolution operator is obtained from the time dependent Schrödinger equation after separating the time and spatial parts of the wave equation:
The solution to this differential equation depends on the form of .
If we know the time evolution operator, , and the initial state of a particular system, all that is needed is to apply to the initial state ket. We then obtain the ket for some later time.
Therefore, if we know the initial state of a system, we can obtain the expectation value of an operator, A, at some later time:
We can make a redefinition by claiming that
and taking as our state kets the time independent, initial valued state ket .
This formulation of quantum mechanics is called the Heisenberg picture. In this picture, operators evolve in time and state kets do not. (Note that the difference between the two pictures only lies in the way we write them down).
In classical physics we obviously have time evolution of a system - our observable (position or angular momentum or whatever variable we are considering) changes in a way dictated by the classical equations of motion. We do not talk about state kets in classical mechanics. Therefore, the Heisenberg, where the operator changes in time, is useful because we can see a closer connection to classical physics than with the Schrödinger picture.
Comparing the Heisenberg Picture and the Schrodinger Picture
As mentioned above, both the Heisenberg representation and the Schrodinger representation give the same results for the time dependent expectation values.
In the Schrodinger picture, in which we are most accustom to, to find the time dependent expectation values of a given operator, the states change over time while the operator remains constant. When the Hamiltonian is independent of time it is possible to write:
as the state at a time t = 0.
At another time t, this becomes
,
which in this form solves the Schrodinger equation
.
Conversely, in the Heisenberg picture to find the time dependent expectation of a given operator, the states remain constant while the operators change in time. In this case, you can write the time dependent operator as:
,
which means the expectation value is,
.
The Heisenberg Equation of Motion
In the Heisenberg picture, the quantum mechanical observables change in time as dictated by the Heisenberg equations of motion. We can study the evolution of a Heisenberg operator by differentiating equation 2 with respect to time:
The last equation is known as the Ehrenfest Theorem.
For example, if we have a hamiltonian of the form,
then we can find the Heisenberg equations of motion for p and r.
The position operator in 3D is:
Since the Hamiltonian as given above has a V(r,t) term and a momentum term the two commuators are as follows:
this yields .
To find the equations of motion for the momentum you need to evaluate ,
which equals, .
This yields
These results are, of course, what we would expect if we only knew classical physics, providing another example of how the Heisenberg picture is more transparently similar to classical physics.
In particular, if we apply these equations to the Harmonic oscilator with natural frequency
we can solve the above equations of motion and find
It is important to stress that the above oscillatory solution is for the position and momentum operators.
The Interaction Picture
The interaction picture is a hybrid between the Schrödinger and Heisenberg pictures. In this picture both the operators and the state kets are time dependent. The time dependence is split between the kets and the operators - this is achieved by first splitting the Hamiltonian into two parts: an exactly soluble, well known part, and a less known, more messy "peturbation".
If we want to look at this splitting process, we can say that .
- - > Equation of motion :
If we call firstpart "" and second part "" ,
it turns out :
so;
and this equation of motion evolves with .
Feynman path integrals
The path integral formulation was developed in 1948 by Richard Feynman. The path integral formulation of quantum mechanics is a description of quantum theory which generalizes the action principle of classical mechanics. It replaces the classical notion of a single, unique trajectory for a system with a sum, or functional integral, over an infinity of possible trajectories to compute a quantum amplitude.
The classical path is the path that minimizes the action.
For simplicity, the formalism is developed here in one dimension.
Using the path integral method, the propagator, , is found directly. The amplitude for a particle to start at at and end at at t can be expressed as a path integral
Where is the action for the the path .
The action is given by the time integral of the Lagrangian, just as in classical mechanics
Where is the Lagrangian. Knowing the propagator, we can calculate the probability that a particle in state at t=0 will be in state at time t by taking the absolute value squared.
Explicit evaluation of the path integral for the harmonic oscillator can be found here File:FeynmanHibbs H O Amplitude.pdf
Problems
4.1) Prove that there is a unitary operator , which is a function of , such that for some wavefunction , .
Discrete eigenvalues and bound states. Harmonic oscillator and WKB approximation
Harmonic oscillator spectrum and eigenstates
1-D harmonic oscillator is a particle moving in the potential of the form: where is the "spring constant".
We can see that as , therefore, the wave functions must vanish at infinity for any values of the energy. Consequently, all stationary states are bound, the energy spectrum is discrete and non-degenerate. Furthermore, because the potential is an even function, the parity operator commutes with Hamiltonian, hence the wave functions will be even or odd.
The energy spectrum and the energy eigenstates can be found by either algebraic method using lowering, raising operators or analysis method.
The Hamiltonian of a 1-D harmonic oscillator is:
where is the natural frequency of the oscillator, and .
It will be easy to memorize how to construct lowering and raising operator by factorizing and rewriting as follows:
Then we define:
as the lowering operator, and
as the raising operator. The Hamiltonian can now be written as:
One way to distinguish from is to remember that the ground state wave function is a Gaussian function and will annihilate this state. Given the lowering and raising operators, the following commutation relation can easily be shown:
Now let , and write the eigenstate equation of as .
Now, let's see how and act on an energy eigenstate : For :
This means that is also an energy eigenstate but correspoding to a lower energy, . is therefore the lowering operator.
Similarly,
and is the so-called raising operator.
So, starting from any energy eigenstates, we can construct all other energy eigenstates by applying or repeatedly. Although there is no limit in applying , there is a limit in applying . The process of lowering energy must stop at some point, since . For the eigenstate of lowest energy (the ground state), we have:
This is a first order ordinary differential equation, which can be easily solved, and the result is as follows:
where is a constant, which can be determined from the normalization condition:
Normalized ground state wave function:
The energy spectrum of 1-D harmonic oscillator is:
Excited state wave function
Energy eigenstates with are called excited states. By applying repeatedly
and after normalization process we obtain the wave function for excited states as follows (more details about the normalization process can be found in Griffiths, Introduction to Quantum Mechanics, 2nd Ed. pg 47):
In the position representation
where is the Hermite polynomial
There are two parts in the wave function of excited states: Gaussian function part and Hermite polynomial part. The former accounts for the behavior of the wave function at long distances, while the later accounts for the behavior of the wave function at short distance and the number of nodes of the wave function.
Coherent states
The general states of an harmonic oscillator can be expressed as a superpostion of the energy eigenstates eq=|n>. A class of states that is of particular importance consists of the eigenstates of non-Hermitian lowering operator , with eigenvalue :
where can be any complex number.
Such states are called coherent states. The term coherent reflects their important role in optics and quantum electronics. The following are some properties of coherent states.
Note that it is not possible to construct an eigenstate of because .
I. Coherent states construction.
II. Coherent states normalization.
where is normalization constant.
For any operators A and B which both commute with their commutator, we have:
and similarly,
therefore:
Apply this result for and ( A and B both commute with their commutator because , we have:
III. Inner product of two coherent states
There is an eigenstate of lowering operator eq=a for any complex number . Therefore, we have a set of coherent states. This is NOT an orthogonal set. Indeed, the inner product of two coherent states and can be calculated as follows:
Hence, the set of coherent states is not orthogonal and the distance in a complex plane measures the degree to which the two eigenstates are 'approximately orthogonal'.
Feynman path integral evaluation of the propagator
The propagator for harmonic oscillator can be evaluated as follows:
where is the deviation of possible trajectories about the classical trajectory.
Saddle point action
The classical action can be evaluated as follows:
Where is the kinetic engergy and is the potential energy.
Equation of motion for harmonic oscillator:
and are constants.
At (starting point),.
At (final point),
Substitute:
Substituting, integrating from time 0 to time t and simplifying, we get:
Harmonic fluctuations
Now, let's evaluate the path integral:
Note that the integrand is taken over all possible trajectory starting at point at time , ending at point at time .
Expanding this integral,
where .
Expanding the path trajectory in Fourier series, we have
we may express in the form
where C is a constant independent of the frequency which comes from the Jacobian of the transformation. The important point is that it does not depend on the frequency . Thus, evaluating the integral of,
where C' is a constant directly related to C and still independent of the frequency of motion. Since the first product series in this final expression is also independent of the frequency of motion, we can absorb it into our constant C' to have a new constant, C. Simplifying further,
In the limit , we already know that
Thus,
and
For a more detailed evaluation of this problem, please see Barone, F. A.; Boschi-Filho, H.; Farina, C. 2002. "Three methods for calculating the Feynman propagator". American Association of Physics Teachers, 2003. Am. J. Phys. 71 (5), May 2003. pp 483-491.
Motion in electromagnetic field
Hamiltonian of a particle of charge and mass in an external electromagetic field, which may be time-dependent is given as follows:
where and are the vector and scalar potentials of the electromagnetic field, respectively.
Let's find out the Heisenberg equation of motion for the position and velocity operators.
For we have:
( does not depend on explicitly)
is the equation of motion for the position operator . This equation also defines the velocity operator :
The Hamiltonian can be rewritten as:
The Heisenberg equation of motion for velecity operator is:
(note that does not depend on expicitly)
Let's use the following commutator identity:
Substituting, we get:
Now let's evaluate and :
(sum over all repeated indices)
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle =-\frac{e}{m^2c}\epsilon_{ijk}(p_jA_k(\bold r,t)+A_j(\bold r,t)p_k)}
(because and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p_k}
commute and so do and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A_k}
)
(Switching indices in the second terms)
(because )
where
Substituting and rearranging, we get:
where
Above is the quantum mechanical version of the equation for the acceleration of the particle in terms of the Lorentz force.
These results can also be deduced in Hamiltonian dynamics, due to the similarity between the Hamiltonian dynamics and quantum mechanics.
- A problem about ;[a particle moving in a magnetic field]
WKB
WKB method (Wentzel-Kramers-Brillouin method) is a technique for finding approximations to certain differential equations, including the one dimensional Schrodinger equation. It was developed in 1926 by Wenzel, Kramers, and Brillouin, for whom it was named. The logic is that as , the wavelength, , tends to zero, and any smooth potential is slowly varying in this limit. Therefore, can be thought of as a local quantity . This is a quasi-classical method of solving the Schrodinger equation.
In WKB, for the turning point, where is infinite, we can not say the potential change slowly. Here, the whole theory is bound to fail, a proper handling of the turning points is the most difficult aspect of the WKB approximation. The potential at the turning point is approximated as linear and slowly increasing. Through this way, 1. we can at least solve the Schrodinger Function and get the wave function in this "region". We can use this wave function to connect the WKB wave functions in the two sides of the turning point. 2. We also need to know the valid region for the WKB wave functions.
For V(x) = 0 (or constant) the solutions to the Schrodinger equation are simply plane waves of the form . If the potential varies smoothly, and the energy of the particle is fixed, the wave function can be described locally by writing its plane wave form .
The WKB solution to the Schrodinger equation for a particle in a smoothly varying potential is given by:
for a classically accessible region where E > V(x) and p(x) is real, and is written as:
for a classically inaccessible region where E < V(x).
In both cases is the classical formula for the momentum of a particle with total energy and potential energy given by:
This is an exact solution if x is constant, otherwise it's a local solution for a locally defined wavelength. There must be a condition on the region in space where the wavelength is locally defined to be sure the wavelength does not vary too much and the locally defined wave function is a valid approximation. This condition is that , which is equivalent to writing .
For example, suppose there is a point, x = a which is a classical turning point at a given value of E which separates the regions where E > V(x) and E < V(x). More specifically the classically inaccessible region is to the right of the classical turning point. In the region appropriately close to the turning point the wave functions can be written as:
for x >> a, and
for x << a.
Note that at the classical turning point and the WKB solution diverges, which means it is no longer a valid approximation because the true wave function will not exhibit such divergent behavior. Thus, around each turning point we need to splice the two WKB solutions on either side of the turning point with a "patching" function that will straddle each turning point. Because we only need a solution for this function in the vicinity of the turning points, we can approximate the potential as being linear. If we center the turning point at the origin the we have:
Solving the Schrodinger equation with our now linearized potential leads to the Airy equation whose solution are the Airy functions. Our patching function is then:
where are c-number coefficients and
The key to patching the wavefunction in the region of the turning point is to asymptotically match the patching function to the wavefunctions in the region outside the region of the classical turning point. In the vicinity of the classical turning point,
Since the region of applicability of the WKB approximation is
near the turning point
This implies that the width of the region around the classical turning point vanishes as . Thus, we can come as close to the turning point as we wish with the WKB approximations by taking a limit as approaches zero, as long as the distance from the classical turning point is much less than . Thus, by extending the patching function towards singularity in the direction of the WKB approximated wavefunction, while simultaneously extending the WKB approximated wavefunction toward the classical turning point, it is possible to match the asymptotic forms of the wavefunctions from the two regions, which are then used to patch the wavefunctions together.
This means that it would be useful to have a form of the Airy functions as they approach positive or negative infinity:
And noticing that (for negative )
and
it becomes apparent that our WKB approximation of the wavefunction is the same as the patching function in the asymptotic limit. This must be the case, since as the region of invalidity of the semiclassical wavefunction in the vicinity of the turning point shrinks, while the solution of the linarized potential problem dopends only on the accuracy of the linearity of the potential, and not on . The two regions must therefore overlap.
For example, one can take and then take the limit . The semiclassical solution must hold as we are always in the region of its validity and so must the solution of the linearized potential problem. Note that the argument of the Airy functions at goes to , which is why we need their asymptotic expansion.
Angular momentum
Commutation relations
Multidimensional problems entail the possibility of having rotation as a part of solution. Just like in classical mechanics where we can calculate the angular momentum using vector cross product, we have a very similar form of equation. However, just like any observable in quantum mechanics, this angular momentum is expressed by a Hermitian operator. Similar to classical mechanics we write angular momentum operator as:
Working in the spatial representation, we have as our radius vector, while is the momentum operator.
Using the cross product in Cartesian coordinate system, we get component of in each direction:
Similarly, using cyclic permutation on the coordinates x, y, z, we get the other two components of the angular momentum operator. All of these can be written in a more compact form using Levi-Civita symbol as (the Einstein summation convention is understood here)
with
Or we simply say that the even permutation gives 1, odd permutation -1, else we get 0.
We can immediately verify the following commutation relations:
- (this relation tells us :)
and
For example,
Also note that for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L^2=L_x^2+L_y^2+L_z^2} ,
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [L_\mu,L^2]=[L_\mu,L_\mu^2]+[L_\mu,L_\nu^2]+[L_\mu,L_\rho^2]=0+i\hbar(L_\nu L_\rho+L_\rho L_\nu-L_\rho L_\nu-L_\nu L_\rho)=0 }
Angular momentum as generator of rotations in 3D
Let Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf\alpha\!} represent an infinitesimally small rotation directed along the axis about which the rotation takes place. The changes Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta \mathbf w} (in the radius vector Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf w\!} of the particle) due to such a rotation is:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta \mathbf w=\mathbf{\alpha}\times \mathbf w}
so
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi(\mathbf w+\delta \mathbf w)=(1+\alpha\cdot(\mathbf w\times\nabla))\psi(\mathbf w)}
The expression
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1+\alpha\cdot(\mathbf w\times\nabla)}
is the operator of an infinitesimally small rotation. We recognize the equation
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf w\times\nabla=\frac{i}{\hbar}\mathbf L}
Therefore, the infinitesimal rotation operator is
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf R_{inf}=1+\frac{i}{\hbar}\alpha\cdot\mathbf L}
This expression is only until the first order correction. The actual rotation operator is calculated by applying this operator N times where N goes to infinity. Doing so, we get the rotation operator for finite angle
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf R = e^{\frac{i}{\hbar}\alpha\cdot\mathbf L}}
In this form, we recognize that angular momentum is the generator of rotation. And we can write the equation relating the initial vector before rotation with the transformed vector as
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf w'=e^{\frac{i}{\hbar}\alpha\cdot\mathbf L}\mathbf w e^{-\frac{i}{\hbar}\alpha\cdot\mathbf L}}
This equation also implies that if we have a scalar instead of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf w\!} , it would be invariant. We can also calculate the effect of the unitary operator Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e^{\frac{i}{\hbar}\alpha\cdot\mathbf L}} on the states:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle r_0|e^{\frac{i}{\hbar}\alpha\cdot\mathbf L}\mathbf \hat{\mathbf r} e^{-\frac{i}{\hbar}\alpha\cdot\mathbf L}=\langle r_0|\hat{\mathbf {r'}}=r_0'\langle r_0|}
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Rightarrow \psi'(r_0)=\langle r_0|\psi'\rangle=\langle r_0|e^{\frac{i}{\hbar}\alpha\cdot\mathbf L}|\psi\rangle=\langle r_0'|\psi\rangle=\psi(r_0')}
This is the wavefunction evaluated at a rotated point.
Eigenvalue quantization
The quantization of angular momentum follows simply from the above commutation relations. Define Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta\!} by:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta=L_x^2+L_y^2+L_z^2}
Since Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta\!} is a scalar, it commutes with each component of angular momentum.
Now Define a change of operators as follows:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L_+=L_x+iL_y\!}
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L_-=L_x-iL_y\!}
From the commutation relations we get
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L_+L_-=\beta-L_z^2+\hbar L_z}
Similarly,
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L_-L_+=\beta-L_z^2-\hbar L_z}
Thus,
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [L_+,L_-]=L_+L_--L_-L_+=2\hbar L_z}
And
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [L_z,L_-]=L_zL_--L_-L_z=-\hbar L_-}
Also, It is easy to show that:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [L^2,L_\pm]=0}
Let Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L'_z\!} be an eigenvalue of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L_z\!} .
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \langle L_z'|L_+L_-|L_z'\rangle=(\beta-L_z'^2+\hbar L_z')\langle L_z'|L_z'\rangle}
Since the left hand side of the above equation is the square of the length of a ket, it has to be non-negative. Therefore
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta-L_z'^2+\hbar L_z'\ge0}
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Rightarrow \beta+\frac{\hbar^2}{4}\ge (L_z'-\frac{\hbar}{2})^2}
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Rightarrow \beta+\frac{\hbar^2}{4}\ge 0}
Defining the number by
The inequality 5.1.13 becomes
Similarly, from equation 5.1.10, we get
This result, combined with 5.1.15 shows that
and
From 5.1.12
Now, if , then is an eigenket of belonging to the eigenvalue . Similarly, if , then is another eigenvalue of , and so on. In this way, we get a series of eigenvalues which must terminate from 5.1.16, and can terminate only with the value . Similarly, using the complex conjugate of 5.1.12, we get that are eigenvalues of L'z. Thus we may conclude that is an integral multiple of the Planck's constant, and that the eigenvalues are:
If is an eigenstate of with eigenvalue , then
Which means that or raises or lowers the component of the angular momentum by .
Orbital angular momentum eigenfunctions
Now we construct our eigenfunctions of the orbital angular momentum explicitly. The eigenvalue equation is
in terms of wave functions, becomes:
Solving for the dependence, we find
We construct the dependence using the differential operator representation of
Where the eigenvalues of are:
We proceed by using the property of and , defined by
to find the following equation
Using eq. 5.2.2, we get
And the solution is
where is an arbitrary function of . We can find the angular part of the solution by using . It turns out to be
And we know that are the spherical harmonics defined by
where the function with cosine argument is the associated Legendre polynomials defined by:
with
And so we then can write:
Central forces are derived from a potential that depends only on the distance r of the moving particle from a fixed point, usually the coordinate origin. Since such forces produce no torque, the orbital angular momentum is conserved.
We can rewrite Eq. 5.1 as
As has been shown in 5.1, angular momentum acts as the generator of rotation.
Central forces
Generalized derivation
A central potential only depends on the distance away from the potential's center and is rotationally invariant, not depending on the orientation.
Due to the rotational symmetry, and . This allows us to find a complete set of states that are simultaneous eigenfunctions of , , and . We can label these states by their eigenvalues of .
From this we can get a state of the same energy for a given with a degeneracy of . We can rewrite the Laplacian as
This makes the Schroedinger equation
Using separation of variables, , we get:
Multiplying both sides by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Y_{l^\prime m'}\!} and integrating over the angular dependence reduces the equation to merely a function of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r\!} .
Now if we let Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u_l(r)=rf_l(r)\!} , this gives the radial Schroedinger equation:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(\frac{-\hbar^2}{2m}\frac{\partial^2}{\partial r^2}+\frac{\hbar^2 l(l+1)}{2mr^2}+V(r)\right)u_l(r)=Eu_l(r)}
Due to the boundary condition that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f_l(r)\!} must be finite the origin, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u_l(r)\!} must vanish.
Often looking at the asymptotic behavior of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u_l(r)\!} can be quite helpful.
As Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r\rightarrow 0\!} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V(r)\ll\frac{1}{r^2}\!} the dominating term becomes the centrifugal barrier giving the approximate Hamiltonian:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{-\hbar^2}{2m}\frac{\partial^2}{\partial r^2}+\frac{\hbar^2 l(l+1)}{2mr^2}}
which has the solutions Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u_l(r)\sim r^{l+1},r^{-l}\!} where only the first term is physically possible because the second blows up at the origin.
As Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r\rightarrow\infty\!} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle rV(r)\rightarrow 0} (which does not include the monopole Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{r}} coulomb potential) the Hamiltonian approximately becomes
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{-\hbar^2}{2m}\frac{\partial^2}{\partial r^2}u_l(r)=Eu_l(r)}
letting Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k=-i\sqrt{\frac{2mE}{\hbar^2}}} gives a solution of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u_l(r)=Ae^{kr}+Be^{-kr}\!} , where when Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k\!} is real, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B=0\!} , but both terms are need when Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k\!} is imaginary.
Nomenclature
Historically, the different values of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle l\!} have taken on names:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{cases} l = 0 & \mbox{s-wave (sharp)}\\ l = 1 & \mbox{p-wave (principle)}\\ l = 2 & \mbox{d-wave (diffuse)}\\ l = 3 & \mbox{f-wave (fundamental)} \end{cases} }
Free particle in spherical coordinates
A free particle is a specific case when Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_0=0\!} of the motion in a uniform potential Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V(r)=V_0\!} . So it's more useful to consider a particle moving in a uniform potential. The Schrodinger equation for the radial part of the wave function is:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(-\frac{2m}{\hbar^2}\frac{\partial^2}{\partial r^2}+\frac{2m}{\hbar^2}\frac{l(l+1)}{r^2}+V_0\right)u_l(r)=Eu_l(r)}
let Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k^2=\frac{2m}{\hbar^2}|E-V|} . Rearranging the equation gives
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(-\frac{\partial^2}{\partial r^2}+\frac{l(l+1)}{r^2}-k^2\right)u_l(r)=0}
Letting Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho=kr\!} gives the equation:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(-\frac{\partial^2}{\partial\rho^2}+\frac{l(l+1)}{\rho^2}\right)u_l(\rho)=u_l(\rho)=d_ld_l^+u_l(\rho)}
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle d_l\!} and become the raising and lowering operators:
Being , it can be shown that
For l=0, , giving
Now applying the raising operator to the ground state
Spherical well
Dividing the potential into two regions, and ,
For the term, the centrifugal barrier drops out and the equations become the following
The generalized solutions are
Using the boundary condition, , we find that . The second equation can then be reduced to sinusoidal function where .
for , we know that since as approaches infinity, the wavefunction does not go to zero.
Matching the conditions that at , the wavefunctions and their derivatives must be continuous which results in 2 equations
Dividing the above equations, we find
Solving for , we know that there is no bound state for
Hydrogen atom
The Schrodinger equation for the particle moving in central potential can be represented in a spherical coordinate system as follows:
where is the angular momentum operator and is the reduced mass.
In this case, being invariant under the rotation, the Hamiltonian, , commutes with both Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L^2\!} and . Furthermore, and commute with each other. Therefore, the energy eigenstates can be chosen to be simultaneously the eigenstates of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H\!} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L^2\!} and . Such states can be expressed as the following:
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Y_l^m(\theta,\phi)} is the spherical harmonic, which is the simultaneous eigenstates of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L^2\!} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L_z\!} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u_l(r)\!} substitution is made for simplification.
Substitute (6.2.2) into (6.2.1), and taking into account the fact that:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L^2\psi(r,\theta,\phi)=L^2[R(r)Y_{lm}(\theta,\phi)]=R(r)L^2Y_{lm}(\theta,\phi)=R(r)\hbar^2l(l+1)Y_{lm}(\theta,\phi) =\hbar^2l(l+1)\psi(r,\theta,\phi)}
we have the equation for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u_l(r)\!} :
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left[ -\frac{\hbar^2}{2m}\frac{\partial^2}{\partial r^2}+\frac{\hbar^2}{2m}\frac{l(l+1)}{r^2}+V(r)\right] u_l(r)=Eu_l(r)}
In the hydrogen atom or single electron ion, the potential is the Coulomb potential between the electron and the nucleus:
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z=1\!} for the hydrogen, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z=2\!} for helium ion , etc.
Since we are only concentrating on the bound states, we can take the limits of :
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lim_{r \to 0}u_l(r)\rightarrow r^{l+1}}
where
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a=\sqrt{\frac{-\hbar^2}{2\mu E}}}
If we allow , then the large limit of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r\!} can be expressed as
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u_l(r)\sim e^{-\kappa r}\!}
Using the limits of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u(r)\!} , the wavefunction can be expressed as the following
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u_l(r)=(\kappa r)^{l+1}e^{-\kappa r}W(\kappa r)\!}
To simplify the equation, make a substitution Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho=\kappa r\!} . The equation now turns into
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u_l(\rho)=\rho^{l+1}e^{-\rho}W(\rho)\!}
Plugging eqn into the the Schrodinger and simplifying turns into
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle W(p)\!} can be expressed as an expansion of polynomials
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle W(p)=a_0+a_1 \rho+a_2\rho^2+...=\sum_{k=0}^\infty a_k \rho^k}
The Schrodinger equation is then expressed as
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{k=0}^\infty (a_{k}k(k-1)\rho^{k-2}+2(l+1)k\rho^{k-2}a_k-2\rho^{k-1}a_k k)+\sum_{k=0}^\infty(\rho_0 a_k\rho^{k-1}-2(l+1)a_k\rho^{k-1})=0}
And simplified into
Bring all 's to the same power
which can be expressed in the simplest fractional form as
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{a_{k+1}}{a_k}=\frac{2(k+l+1)-\rho_0}{(k+1)(k+2l+2)}}
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho_0=2(N+l+1)\!} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle N=0,1,2...\!} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle l=0,1,2,...\!}
In the limit of large k
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lim_{k\to\infty}\frac{a_{k+1}}{a_k}\rightarrow\frac{2}{k}}
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_{k+1}=\frac{2}{k}a_k\sim\frac{2^k}{k!}}
this will make
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi(r) \sim e^{kr} \rightarrow\infty}
so we need to break, and make
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_{k+1}=0\!}
from this, we get the energy spectrum.
The fractional form can be expressed as a confluent hypergeometric function
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle _1F_1(a,c,z)=1+\frac{a}{c}\frac{z}{1!}+\frac{a(a+1)}{c(c+1)}\frac{z^2}{2!}+...=\sum_{k=0}^\infty a_k z^k}
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{a_k}{a_{k-1}}=\frac{\frac{a(a+1)(a+2)...(a+k-1)}{c(c+1)(c+2)...(c+k-1)k!}}{\frac{a(a+1)(a+2)...(a+k-2)}{c(c+1)(c+2)...(c+k-2)(k-1)!}}=\frac{a+k-1}{(c+k-1)k}}
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{a_{k+1}}{a_k}=\frac{a+k}{(c+k)(k+1)}}
by comparison, we find that
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c=2(l+1)\!}
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a=-N\!}
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z=2\rho\!}
So the solution of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle W(\rho)\!} is
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle W(\rho)=constant _1F_1(-N,2(l+1),2\rho)\!}
where :Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho=\kappa r=\sqrt{\frac{-2\mu E}{\hbar^2}}r} Full wavefunction solution with normalization is
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi_{n,l,m}(r,\theta,\phi)=\frac{e^{-\kappa r}(2\kappa r)^l}{(2l+1)!}\sqrt{\frac{(2\kappa)^3(n+l)!}{2n(n-l+1)}}\ _1F_1(-n+l+1,2(l+1),2\kappa r)Y_{lm}(\theta,\phi)}
The first couple of normalized wavefunctions for the hydrogen atom are as follows
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi_{100}= \dfrac{e^{-r/a_o}}{\sqrt{\pi a_o^3}}}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi_{200}= \dfrac{e^{-r/2a_o}}{\sqrt{32\pi a_o^3}} \left( 2-\dfrac{r}{a_o} \right)}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi_{210}= \dfrac{e^{-r/2a_o}}{\sqrt{32\pi a_o^3}} \left( \dfrac{r}{a_o} \right) cos(\theta)}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi_{2 \pm 10}= \dfrac{e^{-r/2a_o}}{ \sqrt{64\pi a_o^3}} \left( \dfrac{r}{a_o} \right) sin(\theta) e^{\pm i \phi}}
The energy is then found to be
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E=-\frac{Z^2 e^4 \mu}{2\hbar^2 n^2}=-\frac{Z^2}{n^2}Ry}
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Ry=13.6 eV\!}
for the hydrogen atom and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n=1,2,3,...\!}
and the degeneracy for each level is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n^2\!}
.
Below is a chart depicting the energy levels possible for the hydrogen atom for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n=1, 2, 3\!}
. The parenthesis indicate the degeneracy.
Continuous eigenvalues and collision theory
Differential cross-section and the Green's function formulation of scattering
Much of what we know about forces and interactions in atoms and nuclei has been learned from scattering experiments, in which say atoms in the target are bombarded with beams of particles. These particles are scattered by the target atoms and then detected as a function of a scattering angle and energy. From theoretical point of view, we are now concerned with the continuous part of the energy spectrum. We are free to choose the value of the incident particle energy and by a proper choice of the zero of energy, this corresponds to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E>0\!} an to eigenfunctions of the unbound states. Before, when we were studying the bound states, the focus was on the discrete energy eigenvalues which allow a direct comparison of theory and experiments. In the continuous part of the spectrum, as it comes into play in scattering, the energy is given by the incident beam, and intensities are the object of measurement and prediction. These being the measures of the likelihood of finding a particle at certain places, are of course related to the eigenfunctions, rather than eigenvalues. Relating observed intensities to calculated wave functions is the first problem in scattering theory.
Figure 1: Collimated homogeneous beam of monoenergetic particles, long wavepacket which is approximately a planewave, but strictly does not extend to infinity in all directions, is incident on a target and subsequently scattered into the detector subtending a solid angle Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle d\Omega\!} . The detector is assumed to be far away from the scattering center.
If Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I_0\!} is the number of particles incident from the left per unit area per time and the number of those scattered into the cone per time, then the differential cross section is defined as
There exist two different types of scattering; elastic scattering, where the incident energy is equal to the detected energy and inelastic scattering which arises from lattice vibrations within the sample. For inelastic scattering, one would need to tune the detector detect where results from the quantum lattice vibrations. For simplification purposes we will only be discussing elastic scattering.
To describe this experiment, start with the stationary Schrodinger equation:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Rightarrow (\nabla^2+k^2)\psi(r)=\frac{2mV(r)}{\hbar^2}\psi(r)}
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E=\frac{\hbar^2k^2}{2m}} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V(r)\!} will be assumed to be finite in a limited region of space Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r<d\!} . This is called the range of the force, e.g. nuclear forces Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle d\sim10^{-15}m\!} , atomic forces Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle d\sim10^{-10}m\!} . Outside this range of forces. the particles move essentially freely. Our problem consists in finding those solutions of the above differential equation which can be written as a superposition of an incoming and an outgoing scattered waves. We found such solutions by writing the Schrodinger differential equation as an integral equation:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi_k=\psi_k^{(0)} +\int d^3r'G_k(\mathbf r,\mathbf r')\frac{2m}{\hbar^2}V(r')\psi_k(r')}
where the Green's function satisfies
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (\nabla^2+k^2)G_k(\mathbf{r},\mathbf{r'})=\delta(\mathbf{r}-\mathbf{r'})}
and
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (\nabla^2+k^2 )\psi^{(0)}_k(x) =0}
and the solution is chosen such that the second term in Eq.(2) corresponds to an outgoing wave. Then
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G_{k}(\mathbf r,\mathbf r')=-\frac{1}{4\pi}\frac{e^{ik|r-r'|}}{|r-r'|}}
and in the asymptotic limit of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r\to\infty\!} :
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lim_{r \to \infty} \psi_k(\mathbf{r})=\psi_k^{(0)}(\mathbf{r}) -\frac{m}{2\pi\hbar^2 }\int d^3\mathbf{r'}e^ {-ik\mathbf{\hat{r}}\cdot\mathbf{r'}}V(\mathbf{r'})\psi_k(\mathbf{r'})\frac{e^ { ik\mathbf{r}}}{r}=\psi_k^{(0)}(\mathbf{r})+f_k(\theta,\phi)\frac{e^ { ik\mathbf{r}}}{r}}
where the scattering amplitude
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f_k(\theta,\phi)=-\frac{m}{2\pi\hbar^2 }\int d^3\mathbf{r'}e^ { -ik\mathbf{\hat{r}}\cdot\mathbf{r'}}V(\mathbf{r'})\psi_k(\mathbf{r'})}
and the angles Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta\!} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi\!} are the angles between Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{r}\!} (the vector defining the detector) and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{k}\!} (the vector defining the in the incoming wave). Now the differential cross section is written through the ratio of the (outgoing) radial current density Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle j_r\!} and the incident current density Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle j_{inc}\!} as
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{d\sigma}{d\Omega}=\frac{j_r r^2}{j_{inc}}}
The radial current is
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle j_r=\frac{\hbar}{2mi}(\psi_{sc}^*\frac{\partial \psi_{sc}}{\partial r}-\psi_{sc}\frac{\partial \psi_{sc}^*}{\partial r})=\frac{\hbar k}{mr^2}|f_k(\theta,\phi)|^2}
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Rightarrow \frac{d\sigma}{d\Omega}=|f_k(\theta,\phi)|^2}
Finally we have 1st Born approximation. For large Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r\!} we find
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi_k(\mathbf{r})\approx\psi_k^{(0)}(\mathbf{r}) -\frac{m}{2\pi\hbar^2 }\int d^3\mathbf{r'}e^ {-ik\mathbf{\hat{r}}\cdot\mathbf{r'}}V(\mathbf{r'})\psi_k^{(0)}(\mathbf{r'})\frac{e^ { ik\mathbf{r}}}{r}}
and
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f_k(\theta,\phi)=-\frac{m}{2\pi\hbar^2 }\int d^3\mathbf{r'}e^ { -ik\mathbf{\hat{r}}\cdot\mathbf{r'}}V(\mathbf{r'})e^{i\mathbf{k}\cdot \mathbf r'}}
Central potential scattering and phase shifts
Recall that for scattering we have Green function method
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi_k =\psi_k^{(0)} +\int d^3 r' G(\mathbf r,\mathbf r')V(\mathbf r')\psi_k (\mathbf r')}
where the Green's function satisfies that
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (\nabla^2+k^2)G_k(\mathbf{r},\mathbf{r'})=\delta(\mathbf{r}-\mathbf{r'})}
and the solution is chosen such that the second term in Eq.(1) corresponds to an outgoing wave.
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle G_k(\mathbf{r},\mathbf{r'})=-\frac{1}{4\pi}\frac{e^ { ik| \mathbf{r}-\mathbf{r'}|}}{|\mathbf{r}-\mathbf{r'}|}}
and in the asymptotic limit of r come to infinity
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lim_{r \to \infty}| \mathbf{r}-\mathbf{r'}|=r-\mathbf{r}\cdot\mathbf{r'}}
Thus
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lim_{r \to \infty} \psi_k(\mathbf{r})=\psi_k^{(0)}(\mathbf{r}) -\frac{m}{2\pi\hbar^2 }\int d^3\mathbf{r'}e^ { -ik\mathbf{\hat{r}}\cdot\mathbf{r'}}V(\mathbf{r'})\psi_k(\mathbf{r'})\frac{e^ { ik\mathbf{r}}}{r} =\psi_k^{(0)}(\mathbf{r})+f_k(\theta,\phi)\frac{e^ { ik\mathbf{r}}}{r}}
where
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f_k(\theta,\phi)=-\frac{m}{2\pi\hbar^2 }\int d^3\mathbf{r'}e^ { -ik\mathbf{\hat{r}}\cdot\mathbf{r'}}V(\mathbf{r'})\psi_k(\mathbf{r'})}
and the angles Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta\!} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi\!} are the angles between Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{r}\!} (the vector defining the detector) and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{k}\!} (the vector defining the in the incoming wave).
For central potentials, i.e. if Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V(r)=V(|\mathbf{r}|)} , then Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f_k(\theta)\!} , i.e. the scattering amplitude does not depend on the azimuthal angle Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi\!} . To determine Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f_k(\theta)\!} we need to find the solution of the Schrodinger equation:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left( -\frac{\hbar^2 }{2m}\nabla^2+V(|\mathbf{r}|) \right) \psi=\frac{\hbar^2 k^2 }{2m}\psi}
we use spherical coordinates
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left( -\frac{\hbar^2 }{2m}\frac{\partial^2 }{\partial r^2 }+\frac{h^2 l(l+1)}{2mr^2}+V(|\mathbf{r}|) \right) u_l(r) =\frac{\hbar^2 k^2 }{2m}u_l(r)}
For Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V(r)\!} with a finite range Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle d\!} , we have shown that for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r \gg d\!} we have
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left( -\frac{\hbar^2 }{2m}\frac{\partial^2 }{\partial r^2 }+\frac{\hbar^2 l(l+1)}{2mr^2} \right) u_l(r) =\frac{\hbar^2 k^2 }{2m}u_l(r)}
and the solution is a combination of spherical Bessel and Neumann functions
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{u(r)}{r}=A_l j_l(kr) +B_l n_l(kr)}
when Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r\!} is large enough we use approximation of Bessel function and Neumann function.
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{u(r)}{r}\rightarrow A_l \frac{\sin(kr-l\frac{\pi}{2})}{kr} -B_l \frac{\cos(kr-l\frac{\pi}{2})}{kr}}
Letting
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{B_l }{A_l }=-\tan\delta_l}
here Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta_l\!} is called phase shift. we can rewrite the above expression (up to a normalization constant) as
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{u_l(r) }{r}\rightarrow\frac{\sin(kr-l\frac{\pi}{2})}{kr}}
Now since we are seeking the scattering amplitude with azimuthal symmetry, we can write the solution of the Schrodinger equation as a superposition of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m=0\!} spherical harmonics only:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi=\sum_{l=0}^{\mathop{ \infty}}a_l(k)P_l(\cos\theta) \frac{u_l(r) }{r}}
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi=\sum_{l=0}^{\mathop{ \infty}}a_l(k)P_l(\cos\theta) \frac{\sin(kr-l\frac{\pi}{2}+\delta_l )) }{kr}}
where the Legendre polynomials are
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P_l(x)= \frac{1}{2^ll!}\frac{d^l }{dx^l }(x^2-1 )^l}
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P_0(x)=1;P_1(x)=x;P_2(x)=\frac{1}{2}(3x^2 -1)}
let us fix the coeffcients Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_l(k)\!} by
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e^{ik\cos\theta}+f_k(\theta,\phi)\frac{e^ { ik\mathbf{r}}}{r}=\sum_{l=0}^{\mathop{ \infty}}a_l(k)P_l(\cos\theta) \frac{\sin(kr-l\frac{\pi}{2}+\delta_l )) }{kr}}
which must hold at large Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r\!} and where we chose the coordinates by letting the incident wave propagate along z-direction. Note that (due to an entirely separate argument):
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e^{ikr\cos\theta}=\sum_{l=0}^{\mathop{ \infty}}(2l+1)i^l P_l(\cos\theta) \frac{\sin(kr-l\frac{\pi}{2} ) }{kr}}
so
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{l=0}^{\mathop{ \infty}}(2l+1)i^l P_l(\cos\theta) \frac{\sin(kr-l\frac{\pi}{2} ) }{kr}+f_k(\theta,\phi)\frac{e^ { -ik\mathbf{r}}}{r}=\sum_{l=0}^{\mathop{ \infty}}a_l(k)P_l(\cos\theta) \frac{\sin(kr-l\frac{\pi}{2}+\delta_l )) }{kr}}
We fix the coefficients Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_l(k)\!} by matching the incoming spherical waves on both sides of the above equation. Note that this does not involve Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f_k(\theta)\!} since the scattering amplitude controls the outgoing spherical wave. Since Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \cos x=(e^{ix} -e^{-ix})/2\!} we have
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_l(k)=(2l+1)i^le^{i\delta_l}}
Therefore:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f_k(\theta)=\frac{1}{k}\sum_{l=0}^{\infty}(2l+1)e^{i\delta_l }\sin\delta_lP_l(\cos\theta)}
Note that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta_l\!} is a function of k and therefore a function of the incident energy. If Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta_l\!} is known we can reconstruct the entire scattering amplitude and consequently the differential cross section. The phase shifts must be determined from the solution of the Schrodinger equation.
Physically, we expect Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta_l < 0\!} for repulsive potentials and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta_l > 0\!} for attractive potentials. Also, if Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle l/k \gg d\!} , then the classical impact parameter is much larger than the range of the potential and in this case we expect Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta_l\!} to be small.
The differential scattering cross section is
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{d\sigma}{d\Omega}=|f_k(\theta) |^2=\frac{1}{k^2 }|\sum_{l=0}^{\infty}(2l+1)e^{i\delta_l }\sin\delta_lp_l(\cos\theta) |^2}
By integrating Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{d\sigma}{d\Omega}} over the solid angle we obtain the total scattering cross section
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma_{tot}=\frac{4\pi}{k^2 }\sum_{l=0}^{\mathop{ \infty}}(2l+1)\sin^2\delta_l}
which follows from the orthogonality of the Legendre polynomials
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int_{-1}^{1}dxP_l(x) P_l'(x)=\frac{2}{(2l+1)}\delta_{ll }}
Finally note that since Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P_l(1) = 1\!} for all Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle l\!} , we have
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma_{tot}=\frac{4\pi}{k}\Im mf(0)}
here we take the imaginary part. This relationship is known as the optical theorem.
Born approximation and examples of cross-section calculations
Recall the scattering of a particle in a potential Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V(r)\!} has a differential cross section of:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{d\sigma}{d\Omega}=|f_k(\mathbf{\hat{r}})|^2}
The scattering amplitude, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f_k(\mathbf{\hat r})\!} , is the coefficient of the outgoing wave.
The Born approximation, often called the first Born approximation, is a technique to find solutions when Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V(r)\!} is small.
The scattering amplitude can be approximated by
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f_k(\mathbf{\hat r})\approx -\frac{m}{2\pi\hbar^2 }\int d^3\mathbf{r'}e^ {-i(k\mathbf{\hat{r}}-\mathbf{k})\cdot\mathbf{r'}}V(\mathbf{r'})}
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -ik\mathbf{\hat r}\!} is the scattered portion and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i\mathbf k\!} is the incident portion.
The scattering amplitude is defined as the coefficient of the outgoing wave in the asymptotic solution (for large Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r\!} )
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi_k(r)\approx N(e^{ikr}+\frac{e^{ikr}}{r}f_k(r))}
of the Schrodinger equation:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (\nabla^2+k^2)\psi=\frac{2m}{\hbar^2}V\psi}
For a central-force potential Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V(r)\!} , the Born scattering amplitude reduces to
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f_B(\theta)=-\frac{m}{2\pi\hbar^2}\int V(r)e^{-iqr}d^3r}
Which leads to the Born cross section:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (\frac{d\sigma}{d\Omega})_B=(\frac{m}{2\pi\hbar^2})^2|\langle K_s|r|K_i\rangle|^2}
Born Approximation for Spherically Symmetric Potentials:
Given spherically symmetry we may define
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf \kappa=\mathbf{k'}-\bold{k}}
and align the polar axis for the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r\!} integral lie along this quantity. We then have:
Our first Born integration then takes the form:
The phi integral introduces a trivial . For the integral we can use the following identity:
and get:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(\theta)\approx -\frac{2m}{\hbar^2\kappa}\int_0^\infty V(r)r\sin(\kappa r) dr}
where the angular dependence of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(\theta)\!} is carried by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \kappa\!} :
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \kappa=2k\sin\frac{\theta}{2}}
Example 1:
Consider the scattering amplitude from a Gaussian potential of the form
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V(r)=Ae^{-\alpha r^2}}
Our scattering amplitude then becomes:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(\theta)\approx \frac{-2mA}{\hbar^2\kappa}\int_0^\infty re^{-\alpha r^2}\sin(\kappa r)dr}
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle =\frac{-2mA}{\hbar^2\kappa}\int_0^\infty \frac{d}{dr}(\frac{-1}{2\alpha}e^{-\alpha r^2})\sin(\kappa r)dr}
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle =\frac{mA}{\alpha\hbar^2\kappa}(0-\kappa\int_0^\infty e^{-\alpha r^2}\cos(\kappa r)dr)}
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle =\frac{-mA}{\alpha\hbar^2}\frac{\sqrt{\pi}}{2\sqrt{\alpha}}e^{-\frac{\kappa^2}{4\alpha}}}
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle =-\frac{mA\sqrt{\pi}}{2\hbar^2\alpha^{\frac{3}{2}}}e^{-\frac{\kappa^2}{4\alpha}}}
Coulomb potential scattering
Example 1
Lets look at an example of a Screened Coulomb (Yukawa) Potential, where we have a potential:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V(r)=V_0e^{-\alpha r}\frac{1}{r}}
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Rightarrow f=\frac{-m}{2\pi\hbar^2}\int_0^\infty dr' r'^2 2\pi\frac{e^{-i|k'-k|r'}-e^{i|k-k'|r'}}{-i|k'-k|r'}\frac{V_0e^{-\alpha r'}}{r'}}
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Rightarrow f=\frac{-2mV_0}{\hbar^2}\int_0^\infty dr' r'^2 \frac{\sin(|k'-k|r')}{|k'-k|r'}\frac{e^{-\alpha r'}}{r'}}
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Rightarrow f=\frac{-2mV_0}{\hbar^2}\frac{1}{(k'-k)^2+\alpha^2}=\frac{-2mV_0}{\hbar^2}\frac{1}{4k^2\sin^2\frac{\theta}{2}+\alpha^2}}
thus we have the differential cross section:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{d\sigma}{d\Omega}= \left( \frac{2mV_0}{\hbar^2} \right) ^2 \left( \frac{1}{4k^2\sin^2\frac{\theta}{2}+\alpha^2}\right) ^2}
Example 2
When we are considering scattering due to the Coulomb potential, we can not neglect the effect of this potential at large distances because it is only a Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{r}} potential.
Use a change of coordinates from Cartesian to parabolic coordinates:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \xi=\sqrt{x^2+y^2+z^2}-z}
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \eta=\sqrt{x^2+y^2+z^2}+z}
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi=\tan^{-1}(\frac{y}{x})}
The following is a picture of parabolic coordinates:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi\!} represents rotation about the z-axis, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \xi\!} represents the parabolas with their vertex at a minimum, and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \eta\!} represents parabolas with their vertex at a maximum.
So now we can write the Schrodinger equation in parabolic coordinates:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left[ \frac{\hbar^2}{2\mu}\frac{4}{\xi+\eta} \left( \frac{\partial}{\partial \xi}\xi\frac{\partial}{\partial \xi}+\frac{\partial}{\partial \eta}\eta\frac{\partial}{\partial \eta}+\frac{\xi+\eta}{4\xi\eta}\frac{\partial^2}{\partial \phi^2} \right) -\frac{2Ze^2}{\xi+\eta} \right] \psi=\frac{\hbar^2k^2}{2\mu}\psi}
So we will seek solutions which are independent of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi\!} . Recall that the scattering amplitude is a function of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta\!} only.
Look for solutions of the form:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left[ \xi\frac{\partial^2}{\partial \xi^2}+(1-ik\xi)\frac{\partial}{\partial \xi}+\frac{Ze^2\mu}{k\hbar^2}k \right]\Phi(\xi)=0}
We can tidy up the notation a little bit by using the following substitution:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda=\frac{Ze^2\mu}{k\hbar^2}}
Now let:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi(\xi)=\sum_{n=0}^\infty a_n \xi^n}
From this we can write:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{a_{n+1}}{a_{n}}=\frac{in-\lambda}{(n+1)^2}k=\frac{n+i\lambda}{(n+1)^2}ik}
Recall the confluent hypergeometric function:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle _1F_1(a,c,z)=1+\frac{a}{c}z+\frac{a(a+1)}{c(c+1)}\frac{z^2}{2!}+\dots+\frac{a(a+1)\dots(a+n-1)}{c(c+1)\dots(c+n-1)}\frac{z^n}{n!}+\dots}
We can then write the recursion formula as the following:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \dfrac{\alpha_{n+1}}{\alpha_n}= \left( \dfrac{a+n}{c+n} \right) \dfrac{1}{n+1}}
This implies that:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi(\xi)=A_1F_1(i\lambda,1,ik\xi)\!}
where the confluent geometric function is written in terms of three new variables, and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A\!} is a c-number.
Now we can write the wavefunction due to Coulomb scattering:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi(r,z)=A_1F_1(i\lambda,1,ik\xi)e^{ikz}\!}
Now we should look at the limit where z is taken to go to infinity, and our confluent hypergeometric function is rewritten as:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle _1F_1(a,c,z)=\frac{\Gamma(c)(-z)^a}{\Gamma(c-a)} \left[ 1-\frac{a(a-c+1)}{2} \right] +\frac{\Gamma(c)}{\Gamma(n)}e^zz^{a-c}}
Now we can use this to rewrite our equation for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi\!} of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \xi\!} :
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Phi(\xi)=Ae^{\frac{-\pi}{2}\lambda} \left[ \frac{e^{-i\lambda \ln(k\xi)}}{\Gamma(1-i\lambda)} \left( 1-\frac{\lambda^2}{ik\xi} \right) +\frac{i\lambda}{ik\xi}\frac{e^{ik\xi-i\lambda \ln(k\xi)}}{\Gamma(1+i\lambda)} \right] }
Rewriting our wavefunction Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi\!} :
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi(r,\theta)=\frac{Ce^{\frac{-\pi\lambda}{2}}}{\Gamma(1-i\lambda)} \left[ \left( 1-\frac{\lambda^2}{2ikr}\frac{1}{\sin^2\frac{\theta}{2}} \right) e^{ikz}e^{-i\lambda \ln(k(r-z))}+\frac{f(\theta)}{r}e^{ikr+i\lambda \ln(2kr)} \right] }
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(\theta)\!} is the following:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(\theta)=\frac{\lambda\Gamma(1-i\lambda)}{2k\Gamma(1+i\lambda)}\frac{1}{\sin^2\frac{\theta}{2}}e^{i\lambda \ln(\sin^2\frac{\theta}{2})}=\frac{\lambda\Gamma(1-i\lambda)}{2k\Gamma(1+i\lambda)} \left( \sin^2\frac{\theta}{2} \right) ^{i\lambda-1}}
We can then get our differential cross section from that by squaring it:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{d\sigma}{d\Omega}=|f(\theta)|^2=\frac{\lambda^2}{4k^2\sin^4(\frac{\theta}{2})}=\frac{(Ze^2)^4}{16E^2}\frac{1}{\sin^4(\frac{\theta}{2})}}
If we normalize the wavefunction to give unit flux at large distances, we must take the following for the constant Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C\!} :
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C=\sqrt{\frac{\mu}{\hbar k}}\Gamma(1-i\lambda)e^{\frac{\pi\lambda}{2}}}
So the wavefunction at large distances is given by the following:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\psi(0)|^2=|C|^2=\frac{\mu}{\hbar k}|\Gamma(1-i\lambda)|^2e^{\pi\lambda}}
where
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\Gamma(1-i\lambda)|^2=\frac{2\pi|\lambda|e^{-\pi\lambda}}{e^{-2\pi\lambda}-1}}
Plugging this in for our wavefunction squared:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\psi(0)|^2=\frac{2\pi|\lambda|}{\frac{\hbar k}{\mu}|1-e^{-2\pi\lambda}|}}
Now let's use the following quantity to represent the velocity:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\hbar k}{\mu}=v}
For small incident velocities, we can write:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\psi(0)|^2=\frac{2\pi Ze^2}{\hbar^2 v^2}}
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\psi(0)|^2=\frac{2\pi Ze^2}{\hbar^2 v^2}e^{-2\pi\frac{Ze^2}{\hbar v}}}
where the first equation is for an attractive Coulomb potential, and the second equation is for a repulsive Coulomb potential.
Two particle scattering
Classically, if we wish to consider a collection of identical particles, say billiard balls, it is always possible to label all the balls such that we can follow a single ball throughout interacting with others. We could, for example, label each ball with a different color. Then, after an arbitrary number of interactions, we can distinguish, say, a red ball from any other. It is not, however, possible to attach such labels to quantum mechanical systems of, say, electrons. Quantum mechanical particles are far to small to attach such physical labels and there are not enough degrees of freedom to label each particle differently. Again considering the classical case, one could imagine simply recording the position of a given particle throughout its trajectory to distinguish it from any other particle. Quantum mechanically, however, we again fail in following a single particles trajectory since each time we make a measurement of position we disturb the system of particles in some uncontrollable fashion. If the wave functions of the particles overlap at all, then the hope of following a single particles trajectory is lost. We now attempt to study the consequences of such indistinguishably between identical quantum particles.
Scattering of Identical Particles
Let's look at the case of two identical bosons (spin 0) from their center of mass frame. To describe the system, we must use a symmetrized wave function. Under the exchange Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r_1\leftrightarrow r_2\!} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r_{cm} = (r_1 + r_2)/2\!} is invariant while Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r = r_1-r_2\!} changes sign. So the center of mass wave function is already symmetric. Furthermore, the wave function has even parity. This implies that the only possible eigenstates of angular momentum of the two particles are those with even angular momentum quantum numbers. This is evident from the property of the associated Legendre polynomials.
But we have to symmetrize Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi(r)\!} by hand:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Y_{lm}(-r)=(-1)^lY_{lm}(r)\!}
Under the transformation:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r\rightarrow -r, \theta\rightarrow\pi-\theta, \phi\rightarrow\phi+\pi}
The first two terms of the symmetrized wave function represent the incident waves corresponding to the center of mass frame. Note that because we are considering identical particles we cannot distinguish the target particle from the incident one. Thus, each particle has equal amplitude of being either one.
The scattering amplitude is:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f_{sym}(\theta,\phi)=f(\theta,\phi)+f(\pi-\theta,\phi+\pi)\!}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta\!} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \pi-\theta\!} can then be associated with the angle through which each particle is scattered. The total amplitude for particles to emerge at each angle is then exactly the sum of amplitudes for emerging at each angle, which is given above. The scattering amplitude remains consistent with the fact that we have two identical particles, and this gives us the differential cross section:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{d\sigma}{d\Omega}=|f(\theta,\phi)+f(\pi-\theta,\phi+\pi)|^2=|f(\theta,\phi)|^2+|f(\pi-\theta,\phi+\pi)|^2+2\Re e[f(\theta,\phi)f^*(\pi-\theta,\phi+\pi)]}
Note:
The first two terms in the differential cross section is what we would get if we had two distinguishable particles, while the third term give the quantum mechanical interference that goes along with identical particles.
As an example, consider scattering through a 90 degree angle. We then have:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(\theta)=f(\pi-\theta)=f(\frac{\pi}{2})}
Now if the particles are distinguishable, the cross section for observing a scattered particle at 90 degrees is then:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (\frac{d\sigma}{d\Omega})_{dis}=2|f(\frac{\pi}{2})|^2}
Where if the particles are indistinguishable, we see above that we will have:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (\frac{d\sigma}{d\Omega})_{ind}=4|f(\frac{\pi}{2})|^2}
Thus the differential cross-section is exactly twice the distinguishable case when the particles are indistinguishable.
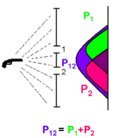








![{\displaystyle i\hbar {\frac {\partial }{\partial t}}\psi (x,t)=\left[-{\frac {\hbar ^{2}}{2m}}{\frac {\partial ^{2}}{\partial x^{2}}}+V(x)\right]\psi (x,t)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c6ed46052f4e829e888f82da9b81c22c50b87a6e)
![{\displaystyle i\hbar \psi ^{*}(x,t){\frac {\partial }{\partial t}}\psi (x,t)=\psi ^{*}(x,t)\left[-{\frac {\hbar ^{2}}{2m}}{\frac {\partial ^{2}}{\partial x^{2}}}+V(x)\right]\psi (x,t)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/26fb15100db06e8f43c5ceeca8053594c8d0ff76)
![{\displaystyle {\frac {\partial }{\partial t}}\psi ^{*}(x,t)\psi (x,t)+\nabla \cdot {\frac {\hbar }{2im}}\left[\psi ^{*}(x,t)\nabla \psi (x,t)-\psi ^{*}(x,t)\nabla \psi (x,t)\right]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5f619e31abd6a17a7730c803968437b64cef02a5)










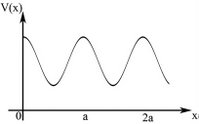

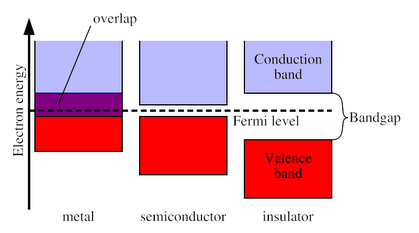




















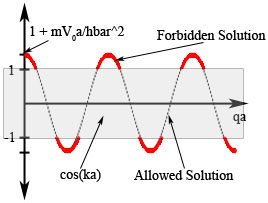
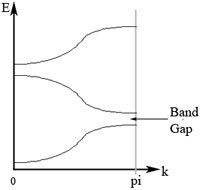
![{\displaystyle [A,B]=AB-BA\,\!.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f24dde05152b3da993659371074bcc97ca735463)
![{\displaystyle \left[A,B\right]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/918f94a9b4c0f131f3c0ea25506dfff16ffb94dd)


![{\displaystyle \left[A,B\right]\neq 0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2c640194838a3094baf1c05a682fdcca2c302285)
![{\displaystyle [A,B]+[B,A]=0\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ae225dc9be2f470bc16a436bfc623d6323e5d45)
![{\displaystyle [A,A]=0\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fcf0417709c1b6d97f3b2cc43f15ffc68ed57334)
![{\displaystyle [A,B+C]=[A,B]+[A,C]\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/66b431f1e7634615fe7a9f5185a0cc6506688f81)
![{\displaystyle [A+B,C]=[A,C]+[B,C]\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/43bb547b5945963c7607533159afa477061592dd)
![{\displaystyle [AB,C]=A[B,C]+[A,C]B\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3260303fa30784e9b7b302a382589e33ba22a9ad)
![{\displaystyle [A,BC]=[A,B]C+B[A,C]\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e7f65e90d08782a020968720cccb195ed5870161)
![{\displaystyle [A,[B,C]]+[C,[A,B]]+[B,[C,A]]=0\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/817ebbb9a1fec2076352ca515d9a3db816cc3e15)



![{\displaystyle [A^{n},B]=nA^{n-1}[A,B]\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f53a983ba3f8f9a53f90fbca65b7bad9d6ae0c86)
![{\displaystyle [A,[A,B]]=[B,[A,B]]=0\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/41fe7a7cd8f5c1530df927927b2fd16e5655fe89)









![{\displaystyle {\hat {A}}{\hat {B}}-{\hat {B}}{\hat {A}}=\left[{\hat {A}},{\hat {B}}\right]=0\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b01800b22b9b744c0be03a19372ee3afe1f80108)




![{\displaystyle \left[{\hat {x}},{\hat {p}}\right]=i\hbar .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5bb7bed896610e130f45045df1c423326bd7b4eb)
![{\displaystyle \left[{\hat {r}}_{i},{\hat {p}}_{j}\right]=i\hbar \delta _{ij}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7e5e480bddd2206b7aa559f4398e9d668ff53f26)
![{\displaystyle \left[{\hat {r}}_{i},{\hat {r}}_{j}\right]=\left[{\hat {p}}_{i},{\hat {p}}_{j}\right]=0,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d6354b70abfca6d1082085e0082da505c0ecb6b3)




![{\displaystyle [A,B]=\sum _{k}\left({\frac {\partial A}{\partial q_{k}}}{\frac {\partial B}{\partial p_{k}}}-{\frac {\partial A}{\partial p_{k}}}{\frac {\partial B}{\partial q_{k}}}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a7e6c94a4a26b141a0631a4640c5e66a3c676c4a)
![{\displaystyle [p_{i},p_{j}]=\sum _{k}\left({\frac {\partial p_{i}}{\partial q_{k}}}{\frac {\partial p_{j}}{\partial p_{k}}}-{\frac {\partial p_{i}}{\partial p_{k}}}{\frac {\partial p_{j}}{\partial q_{k}}}\right)=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9255949165e5328e122c7f903d8d3b1dd7b83918)
![{\displaystyle [q_{i},q_{j}]=\sum _{k}\left({\frac {\partial q_{i}}{\partial q_{k}}}{\frac {\partial q_{j}}{\partial p_{k}}}-{\frac {\partial q_{i}}{\partial p_{k}}}{\frac {\partial q_{j}}{\partial q_{k}}}\right)=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7939bf327ac73866f71b318a9a828fa17dbfad5e)
![{\displaystyle [p_{i},q_{j}]=\sum _{k}\left({\frac {\partial p_{i}}{\partial q_{k}}}{\frac {\partial q_{j}}{\partial p_{k}}}-{\frac {\partial p_{i}}{\partial p_{k}}}{\frac {\partial q_{j}}{\partial q_{k}}}\right)=\sum _{k}-\delta _{ik}\delta _{jk}=-\delta _{ij}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2888b6af72113c70ed0483033ae27730bb37b148)







![{\displaystyle [{\hat {A}},{\hat {B}}]=i{\hat {C}}\;}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3b1ea2be7814af1fb6decd77156d587d74a39026)








![{\displaystyle {\begin{aligned}f(\alpha )&=\langle \psi |(\alpha \Delta {\hat {A}}-i\Delta {\hat {B}})^{\dagger }(\alpha \Delta {\hat {A}}-i\Delta {\hat {B}})|\psi \rangle \\&=\langle \psi |(\alpha \Delta {\hat {A}}+i\Delta {\hat {B}})(\alpha \Delta {\hat {A}}-i\Delta {\hat {B}})|\psi \rangle \\&=\langle \psi |\alpha ^{2}\left(\Delta {\hat {A}}\right)^{2}-i\alpha [\Delta {\hat {A}},\Delta {\hat {B}}]+\left(\Delta {\hat {B}}\right)^{2}|\psi \rangle \\&=\langle \psi |\alpha ^{2}\left(\Delta {\hat {A}}\right)^{2}|\psi \rangle +\langle \psi |\alpha {\hat {C}}|\psi \rangle +\langle \psi |\left(\Delta {\hat {B}}\right)^{2}|\psi \rangle \\&=\alpha ^{2}\langle \left(\Delta {\hat {A}}\right)^{2}\rangle +\alpha \langle {\hat {C}}\rangle +\langle \left(\Delta {\hat {B}}\right)^{2}\rangle \\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/889c4b13f5ca42613e0fabfddb336d0c3f9c6fde)














![{\displaystyle {\frac {d}{dt}}A_{H}={\frac {\partial U^{\dagger }}{\partial t}}AU+U^{\dagger }{\frac {\partial A}{\partial t}}U+U^{\dagger }A{\frac {\partial U}{\partial t}}={\frac {-1}{i\hbar }}U^{\dagger }HAU+\left({\frac {\partial A}{\partial t}}\right)_{H}+U^{\dagger }AHU{\frac {1}{i\hbar }}={\frac {1}{i\hbar }}\left(\left[A,H\right]\right)_{H}+\left({\frac {\partial A}{\partial t}}\right)_{H}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4bdb7392d62bb264e9f0a8f82c0d0238d265dfc9)

![{\displaystyle i\hbar {\frac {d{\hat {r}}(t)}{dt}}=\left[{\hat {r}}(t),H\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6343cbe0d26e6a613672661eece72d568f7ef422)
![{\displaystyle \left[{\hat {r}}(t),V(r,t)\right]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/959bc446dbb5f4eca3cc422e31b93fc78658cab1)
![{\displaystyle \left[{\hat {r}}(t),{\frac {p(t)^{2}}{2m}}\right]={\frac {i\hbar p(t)}{m}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d530dadb68b3ce994f45349e5222a8e8d2c519b5)

![{\displaystyle \left[{\hat {p}}(t),V(r(t))\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ce25dd44b433c45960c0db6436ebbd3914e4ec5a)
![{\displaystyle \left[{\hat {p}},V(r)\right]=-i\hbar \nabla V(r)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ce145712853118db8554991f78bf2c6694022910)














![{\displaystyle {\frac {d}{dt}}A_{I}(t)={\frac {1}{i\hbar }}\left[{A_{I},H_{o}}\right]+{\frac {\partial A_{I}}{\partial t}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/55940660ff13f0562b9be7aabd15049411a5a839)





![{\displaystyle \langle x|{\hat {U}}(t)|x_{0}\rangle =\int _{x_{0}}^{x}Dx(t')e^{iS[x(t')]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/55c1d5552e75fd3bc4b6b7bc5e5aa214f834edca)
![{\displaystyle S[x(t)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ed75d4ae411041a5a76c9b843c723f6c61cfb5f1)

![{\displaystyle S[x(t')]=\int _{0}^{t}dt'{\mathcal {L}}[x(t'),{\dot {x}}(t'),t']}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b196c1692223dd6fbcb4ca3fb0898e92478fe08f)
![{\displaystyle {\mathcal {L}}[x(t'),{\dot {x}}(t'),t']={\frac {1}{2}}m{\dot {x}}^{2}(t')-V(x[t'],t')}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a822bf06d77613f6476e752c1eedd662e317860f)

















![{\displaystyle [{\hat {a}},{\hat {a}}^{\dagger }]=1.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/10235c596afd2a1fe9ee7522ffd66f35dd06618e)































![{\displaystyle e^{A}e^{B}=e^{A+B}e^{{\frac {1}{2}}[A,B]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cab548d9561ef6b750921eeff965bba60c556c72)
![{\displaystyle e^{B}e^{A}=e^{B+A}e^{{\frac {1}{2}}[B,A]}=e^{A+B}e^{-{\frac {1}{2}}[A,B]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c859a951fea3b544eee8b740052feff077e0da66)
![{\displaystyle e^{A}e^{B}=e^{B}e^{A}e^{-[A,B]}\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/06ff435d9743137e1ec6689969570e13d89dc541)


![{\displaystyle [A,B]=|\alpha |^{2})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/09e69b77923685b533d14fa411b68b1a64850df0)

![{\displaystyle N^{2}<0|e^{\alpha a^{+}}e^{\alpha ^{*}a}e^{[\alpha ^{*}a,\alpha a^{+}]}|0>=N^{2}e^{|\alpha |^{2}}<0|e^{\alpha a^{+}}e^{\alpha ^{*}a}|0>}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4be71e96ad7ffc874742a21e4639d8d4d118c3d5)






![{\displaystyle =e^{-{\frac {1}{2}}|\alpha |^{2}}e^{-{\frac {1}{2}}|\beta |^{2}}<0|e^{\alpha a^{+}}e^{\beta ^{*}a}e^{[\beta ^{*}a,\alpha a^{+}]}|0>}](https://wikimedia.org/api/rest_v1/media/math/render/svg/535f370e2b6452adc162cfe84b0637d887a4dd4e)




![{\displaystyle <x|{\hat {U}}(t,0)|x_{0}>=e^{{\frac {i}{\hbar }}S}\int _{y(0)=0}^{y(t)=0}D[y(t')]e^{{\frac {i}{\hbar }}\int _{0}^{t}({\frac {1}{2}}my'^{2}-{\frac {1}{2}}ky^{2})dt'}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/00d098a20301891a5c311fef1138c165dc18583c)











![{\displaystyle KE={\frac {1}{2}}m({\frac {dx_{cl}}{dt}})^{2}={\frac {1}{2}}m[-\omega x_{0}sin(\omega t')+\omega {\frac {x-x_{0}cos(\omega t)}{sin(\omega t)}}cos(\omega t')]^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c03a3aeaade6dc957c3ea3650ea604974dd02621)
![{\displaystyle PE={\frac {1}{2}}k(x_{cl}(t'))^{2}={\frac {1}{2}}k[x_{0}cos(\omega t')+{\frac {x-x_{0}cos(\omega t)}{sin(\omega t)}}sin(\omega t')]^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bb63a7e2d5f8cf082cfa1fb73866ed93147fda8f)

![{\displaystyle A=A(t)=\int _{y(0)=0}^{y(t)=0}D[y(t')]e^{{\frac {i}{\hbar }}\int _{0}^{t}({\frac {1}{2}}my'^{2}-{\frac {1}{2}}ky^{2})dt'}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b7d53bf1d136d3b2adf383e02b2e436ce183bc8f)
![{\displaystyle A(t)=\left({\frac {m}{2\pi i\hbar }}\right)^{\frac {N}{2}}\int _{-\infty }^{\infty }dy_{1}\ldots dy_{N-1}\exp {\left[{\frac {i}{\hbar }}\left({\frac {m}{2\Delta t}}y_{N-1}^{2}-{\frac {\Delta t}{2}}ky_{N-1}^{2}\right)\right]}\exp {\left[{\frac {i}{\hbar }}\left({\frac {m}{2\Delta t}}(y_{N-1}-y_{N-2})^{2}-{\frac {\Delta t}{2}}ky_{N-2}^{2}\right)\right]}\ldots \exp {\left[{\frac {i}{\hbar }}\left({\frac {m}{2\Delta t}}y_{1}^{2}-{\frac {\Delta t}{2}}ky_{1}^{2}\right)\right]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/660b040d7723b0abdb8a4536ef7882f45188cfbf)



![{\displaystyle A(t)=C\int _{-\infty }^{\infty }da_{1}\ldots da_{N-1}\exp {\left[\sum _{n=1}^{N-1}{\frac {im}{2\hbar }}\left(\left({\frac {n\pi }{t}}\right)^{2}-\omega ^{2}\right)a_{n}^{2}\right]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2677009adcea1b5532408d39f84481f680ae544e)

![{\displaystyle A(t)=C'\prod _{n=1}^{N-1}\left[\left({\frac {n\pi }{t}}\right)^{2}-\omega ^{2}\right]^{-{\frac {1}{2}}}=C'\prod _{n=1}^{N-1}\left[\left({\frac {n\pi }{t}}\right)^{2}\right]^{-{\frac {1}{2}}}\prod _{n=1}^{N-1}\left[1-\left({\frac {\omega t}{n\pi }}\right)^{2}\right]^{-{\frac {1}{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d29ee08cd8f26b42913147e6dee0ae372ea08afa)











![{\displaystyle {\frac {d{\mathbf {r}}}{dt}}={\frac {1}{i\hbar }}[{\mathbf {r}},H]={\frac {1}{i\hbar }}[{\mathbf {r}},{\frac {1}{2m}}({\mathbf {p}}-{\frac {e}{c}}{\mathbf {A}}({\mathbf {r}},t))^{2}+e\phi ({\mathbf {r}},t)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/71d498d5b0991c74cad06f08f625887596a7ed10)

![{\displaystyle ={\frac {1}{2im\hbar }}[{\mathbf {r}},({\mathbf {p}}-{\frac {e}{c}}{\mathbf {A}}({\mathbf {r}},t))^{2}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/efedf6ca8f6428d4478ff4e8362874d06dbbaf77)
)+{\frac {1}{2im\hbar }}({\mathbf {p}}-{\frac {e}{c}}{\mathbf {A}}({\mathbf {r}},t))[{\mathbf {r}},{\mathbf {p}}-{\frac {e}{c}}{\mathbf {A}}({\mathbf {r}},t))]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3ca43a31215b30b0f13b736d73bea1d4d0fbf212)
)+{\frac {1}{2im\hbar }}({\mathbf {p}}-{\frac {e}{c}}{\mathbf {A}}({\mathbf {r}},t))[{\mathbf {r}},{\mathbf {p}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0103f165201ea17a2160e859b64829b066a7a600)





![{\displaystyle {\frac {d{\mathbf {v}}}{dt}}={\frac {1}{i\hbar }}[{\mathbf {v}},H]+{\frac {\partial {\mathbf {v}}}{\partial t}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b882cdf357fc6c038237d81870138dbcc57236a9)
![{\displaystyle ={\frac {1}{i\hbar }}[{\mathbf {v}},{\frac {m}{2}}{\mathbf {v}}.{\mathbf {v}}]+{\frac {1}{i\hbar }}[{\mathbf {v}},e\phi ]-{\frac {e}{mc}}{\frac {\partial {\mathbf {A}}}{\partial t}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9a8b557813f8325b8d76ba6683a54d3712ba075c)

![{\displaystyle [{\mathbf {v}},{\mathbf {v}}.{\mathbf {v}}]={\mathbf {v}}\times ({\mathbf {v}}\times {\mathbf {v}})-({\mathbf {v}}\times {\mathbf {v}})\times {\mathbf {v}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e4bd600326eb2f21dd4ee092fe86d1b81182caf7)
![{\displaystyle {\frac {d{\mathbf {v}}}{dt}}={\frac {1}{i\hbar }}{\frac {m}{2}}({\mathbf {v}}\times ({\mathbf {v}}\times {\mathbf {v}})-({\mathbf {v}}\times {\mathbf {v}})\times {\mathbf {v}})+{\frac {1}{i\hbar }}e[{\mathbf {v}},\phi ]-{\frac {e}{mc}}{\frac {\partial {\mathbf {A}}}{\partial t}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/25ba727883a8d4b40c73ddb0e29cf28d66d4c969)

![{\displaystyle [{\mathbf {v}},\phi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/032728e629f76d0caabd6eb9a1646bb474cb44c1)







![{\displaystyle =-{\frac {e}{m^{2}c}}\epsilon _{ijk}[p_{j},A_{k}({\mathbf {r}},t)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/99dec35b3838a10064f647aa4065639747af7993)

![{\displaystyle \rightarrow [{\mathbf {v}}\times {\mathbf {v}}]=i\hbar {\frac {e}{m^{2}c}}(\nabla \times {\mathbf {A}})=i\hbar {\frac {e}{m^{2}c}}{\mathbf {B}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/defd1b1bb42d0bafd530e207d5c7066533a20480)
![{\displaystyle [{\mathbf {v}},\phi ]={\frac {1}{m}}[{\mathbf {p}}-{\frac {e}{c}}{\mathbf {A}}({\mathbf {r}},t),\phi ({\mathbf {r}},t)]={\frac {1}{m}}[{\mathbf {p}},\phi ({\mathbf {r}},t)]={\frac {1}{m}}{\frac {\hbar }{i}}\nabla \phi }](https://wikimedia.org/api/rest_v1/media/math/render/svg/bce7a28b64d00f76767e7e9f9392c453352194f9)









![{\displaystyle \psi (x)\approx {\frac {C}{\sqrt {p(x)}}}\exp \left[{\frac {i}{\hbar }}\int _{x_{0}}^{x}p(x')dx'\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a5d079f9fbfa9a857f0ca545abebbfa1cebc539c)
![{\displaystyle \psi (x)\approx {\frac {C'}{\sqrt {p(x)}}}\exp \left[{\frac {1}{\hbar }}\int _{x_{0}}^{x}p(x')dx'\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/14e7224a03a4ddc2df7c654b8b70d5114687d2ac)






![{\displaystyle \psi (x)\approx {\frac {A}{\sqrt {p(x)}}}\exp \left[{\frac {-1}{\hbar }}\int _{a}^{x}p(x')dx'\right]+{\frac {B}{\sqrt {p(x)}}}\exp \left[{\frac {1}{\hbar }}\int _{a}^{x}p(x')dx'\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6ffe0ff463d05e33af71b5f01447d14aaecd92c5)
![{\displaystyle \psi (x)\approx {\frac {C}{\sqrt {p(x)}}}\exp \left[{\frac {-i}{\hbar }}\int _{a}^{x}p(x')dx'\right]+{\frac {D}{\sqrt {p(x)}}}\exp \left[{\frac {i}{\hbar }}\int _{a}^{x}p(x')dx'\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/47b2986b640cb7f037b7f835305cf8ed2e40308d)





























![{\displaystyle [L_{\mu },r_{\nu }]=i\hbar \epsilon _{\mu \nu \lambda }r_{\lambda }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8fc3ecffa57e7be5d222c02172f33af8f0f2e0ec)
![{\displaystyle [L_{\mu },p_{\nu }]=i\hbar \epsilon _{\mu \nu \lambda }p_{\lambda }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b80d16e78d71c0227cd5b80d0e51d7598948afef)
![{\displaystyle [L_{\mu },L_{\nu }]=i\hbar \epsilon _{\mu \nu \lambda }L_{\lambda }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2ea81179ef2e1eea10bfd8555b91f975a916777b)

![{\displaystyle [{\hat {\mathbf {n} }}\cdot \mathbf {L} ,\mathbf {r} ]=i\hbar (\mathbf {r} \times {\hat {\mathbf {n} }})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c6a650bd8c4fb2e6305ea3ede9d9f8804860146c)
![{\displaystyle [{\hat {\mathbf {n} }}\cdot \mathbf {L} ,\mathbf {p} ]=i\hbar (\mathbf {p} \times {\hat {\mathbf {n} }})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/72447de804c87582234bb8dbefb54fc3b11d365c)
![{\displaystyle [{\hat {\mathbf {n} }}\cdot \mathbf {L} ,\mathbf {L} ]=i\hbar (\mathbf {L} \times {\hat {\mathbf {n} }})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/14f22710e57a97952b9a66a9f7c4e85c7f01a6d0)
![{\displaystyle [L_{\mu },r_{\nu }]=[\epsilon _{\mu \lambda \rho }r_{\lambda }p_{\rho },r_{\nu }]=\epsilon _{\mu \lambda \rho }[r_{\lambda }p_{\rho },r_{\nu }]=\epsilon _{\mu \lambda \rho }r_{\lambda }[p_{\rho },r_{\nu }]=\epsilon _{\mu \lambda \rho }r_{\lambda }{\frac {\hbar }{i}}\delta _{\rho \nu }=\epsilon _{\mu \lambda \nu }r_{\lambda }{\frac {\hbar }{i}}=i\hbar \epsilon _{\mu \nu \lambda }r_{\lambda }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4457a0a8ce46c08f04db8daf086e3c941548c5d3)
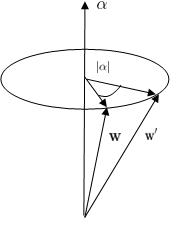























![{\displaystyle L_{z}L_{\pm }|m\rangle =([L_{z},L_{\pm }]+L_{\pm }L_{z})|m\rangle =(\pm \hbar L_{\pm }+L_{\pm }m)|m\rangle }](https://wikimedia.org/api/rest_v1/media/math/render/svg/2d562199c1f5fdcee710a043c8d25fab4a6d8e69)
























![{\displaystyle [H,L_{z}]=0\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dbb0b06c1ff74e5e51e3434e0c47098c062ac8c0)
![{\displaystyle [H,L^{2}]=0\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a45d3b11ba0b00ef92fe4a4b4f4328a5fb7e62ad)