Phy5645

Welcome to the Quantum Mechanics A PHY5645 Fall2008

Schrodinger equation. The most fundamental equation of quantum mechanics which describes the rule according to which a state $|\Psi \rangle$ evolves in time.

This is the first semester of a two-semester graduate level sequence. Its goal is to explain the concepts and mathematical methods of Quantum Mechanics, and to prepare a student to solve quantum mechanics problems arising in different physical applications. The emphasis of the courses is equally on conceptual grasp of the subject as well as on problem solving. This sequence of courses builds the foundation for more advanced courses and graduate research in experimental or theoretical physics.

The key component of the course is the collaborative student contribution to the course Wiki-textbook. Each team of students is responsible for BOTH writing the assigned chapter AND editing chapters of others.

---

Outline of the course:

Physical Basis of Quantum Mechanics

Basic concepts and theory of motion in QM

In Quantum Mechanics, all of the information of the system of interest is contained in a wavefunction , $\Psi \,\!$. Physical properties of the system such as position, linear and angular momentum, energy, etc. can be represented via linear operators, called observables. These observables are a complete set of commuting Hermitian operators, which means that the common eigenstates (in the case of quantum mechanics, the wavefunctions) of these Hermitian operators form an orthonormal basis. Through these mathematical observables, a set of corresponding physical values can be calculated.

In order to clarify the paragraph above, consider an analogous example: Suppose that the system is a book, and we characterize this book by taking measurements of the dimensions of this book and its mass (The volume and mass are enough to characterize this system). A ruler is used to measure the dimensions of the book, and this ruler is the observable operator. The length, width, and height (values) from the measurements are the physical values corresponding to that operator (ruler). For measuring the weight of the book, a balance is used as the operator. The measured mass of the book is the physical value for the corresponding observable. The two observable operators (the ruler and the mass scale) have to commute with each other, otherwise the system can not be characterized at the same time, and the two observables can not be measured with infinite precision.

In quantum mechanics, there are some measurements that cannot be done at the same time. For example, suppose we want to measure the position of an electron. What we would do is send a signal (a gamma ray, for example), which would strike the electron and return to our detectors. We have, then, the position of the electron. But as the photon struck the electron, the electron gained additional momentum, so then our simultaneous momentum measurement could not be precise. Therefore both momentum and position cannot be measured at the same time. These measurement are often called "incompatible observables." This is explained in the Heisenberg uncertainty principle and implies, mathematically, that the two operators do not commute.

This concept contrasts with classical mechanics, where the two observables that do not commute with each other can still be measured with infinite precision. This is because of the difference in dimension of the object: macroscopic (classical mechanics) and microscopic scale (quantum mechanics). However, the prediction of quantum mechanics must be equivalent to that of the classical mechanics when the energy is very large (classical region). This is known as the Correspondence Principle, formally expressed by Bohr in 1923.

We can explain this principle by the following: In quantum mechanics, particles cannot have arbitrary values of energy, only certain discrete values of energy. There are quantum numbers corresponding to specific values of energy and states of the particle. As the energy gets larger, the spacing between these discrete values becomes relatively small and we can regard the energy levels as a continuum. The region where the energy can be treated as a continuum is what is called the classical region.

UV Catastrophy (Blackbody Radiation)

Imagine a perfect absorber cavity (i.e. it absorbs all radiation at all wavelengths, so that its spectral radiance is only going to depend on the temperature). This emission is called the blackbody radiation. This blackbody radiation experiment shows an important failure of classical mechanics. Lord Rayleigh (John William Strutt) and Sir James Jeans applied classical physics and assumed that the radiation in this perfect absorber could be represented by standing waves with nodes at the ends. The result predicts that the spectral intensity will increase quadratically with the increasing frequency, and will diverge to infinite energy or intensity squared at a UV frequency, or so called "Ultraviolet Catastophy."

In 1900, Max Planck offered a successful explanation for blackbody radiation. He also assumed the the radiation was due to oscillations of the electron, but the difference between his assumption and Rayleigh's was that he assumed that the possible energies of an oscillator were not continuous. He proposed that the energy of this oscillator would be proportional to the frequency of a constant, the Planck constant.

$E=h\nu =\hbar \omega$

Here E is energy, h is the Planck constant ($h=6.626*10^{-34}Joule-seconds\!$ ) and $\nu \!$ is the frequency of the oscillator. With the concept of energy being discrete in mind, the result is that Planck's calculation avoided the UV catastrophy, and instead the energy approached zero as the frequency is increased. In summary, the energy of the electromagnetic radiation is proportional to frequency instead of the amplitude of the electromagnetic waves, defying the classical physics where the energy is proportional to the intensity.

Photoelectric Effect

Consider a system composed of light hitting a metal plate. From experimental observations, a current can be measured as light is incident on the metal plate. This phenomenon was first studied by Albert Einstein (1905). During this period, the classical point of view is that an electron is bound inside of an atom, and an excitation energy is needed in order to release it from the atom. This energy can be brought forth in the form of light. The classical point of view also includes the idea that the energy of this light is proportional to its intensity. Therefore, if enough energy (light) is absorbed by the electron, the electron eventually will be released. However, this is not the case.

The determining factor here is not the intensity of the light, but the frequency used on the electron. If the frequency of the light is the "specific" frequency, the electron will be released. This specific frequency of light is in resonance with the energy "frequency" of the electron. Einstein made the conclusion that the energy of a single photon is proportional to its frequency, not the intensity.

Einstein realized that the classical view that light is a wave was not true, but instead light must be a particle. If light were a wave, then the mechanism that the wave transmits its energy is due to its perturbation, which is the amplitude of the wave. The photoelectric effect clearly shows that (amplitude)2 = intensity has no affect on the electron energy, instead, only a specific frequency will have an effect on the energy of the electron. Agreeing with the UV catastrophy conclusions, he stated that light is made of particles called "photons," with an energy equal to hv.

Stability of Matter

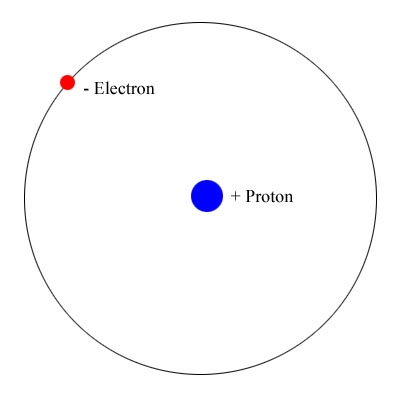
One of the most important problems to inspire the creation of Quantum Mechanics was the model of the Hydrogen Atom. After Thompson discovered the electron, and Rutherford, the nucleus (or Kern, as he called it), the model of the Hydrogen atom was refined to one of the lighter electron of unit negative elementary charge orbiting the larger proton, of unit positive elementary charge. However, it was well known that classical electrodynamics required that charges accelerated by an EM field must radiate, and therefore lose energy. For an electron that moves in circular orbit about the more massive nucleus under the influence of the Coulomb attractive force, here is a simple non-relativistic model of this classical system:

Where $r\,\!$ is the orbital radius, and we neglect the motion of the proton by assuming it is much much more massive than the electron.

So the question is: What determines the rate $\rho$ of this radiation? and how fast is this rate?

The electron in the Bohr's model involves factors of: radius $r_{0}\,\!$, angular velocity $\omega \,\!$, charge of the particle $e\,\!$, and the speed of light, $c\,\!$: $\rho =\rho (r_{0},\omega ,e,c)\,\!$

The radius and charge will not enter separately, this is because if the electron is far from the proton, then the result can only depend on the dipole moment, which is .

Therefore the above parameters is now:

What are the dimensions of $\rho \,\!$?

Essentially, since light is energy, we are looking for how much energy is passed in a given time.

Knowing this much already imposes certain constraints on the possible dimensions. By using dimensional analysis, let's construct something with units of energy.

From potential energy for coulombic electrostatic attractions:

has to be with , multiply by , and divide .

The angular velocity is in frequency, so to get the above equations in energy/time, just multiply it with the angular velocity.

(Here, it is seen that the acceleration of the electron will increase with decreasing orbital radius. The radiation due to the acceleration a is given by the Larmor Formula:

It was known that the hydrogen atom had a certain radius on the order of .5 angstroms. Given this fact it can easily be seen that the electron will rapidly spiral into the nucleus, in the nanosecond scale. Clearly, the model depicts an unstable atom which would result in an unstable universe. A better representation of of an electron in an atom is needed.

Double Slit Experiment

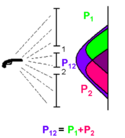
Bullet

Double slit thought experiment with classical bullets

Imagine a rattling gun which is shooting bullets in all directions. A histogram of the bullet's location after it passes through the two slits is plotted. If slit 2 is closed, but the slit 1 is open, then the green peak is observed which is given by the distribution function $p_{1}$. Similarly, if the slit 1 is closed, but he slit 2 is open, the pink peak is observed which is given by the distribution function $p_{2}$. When both slits are open, $peak_{12}$ (purple) is observed. This agrees with the classical view, where the bullet is the particle and $p_{12}$ is simply a sum of $p_{1}$ and $p_{2}$.

The equation describing the probability of the bullet arrival if both of the slit are open is therefore

$p_{12}=p_{1}+p_{2}.$

Classical Waves

Double slit thought experiment with water waves

As waves are passed through the double slit, the intensity of the waves which are proportional to the squares of the height of the wave motion and are observed when slit 1 and 2 are closed respectively. These intensities are similar to the histograms for the bullets in the previous demonstration. However, an interference pattern of the intensity (H12) is observed when both slits are opened. This is due to constructive and destructive interferences of the two waves. The resultant interference is the square of the sum of the two individual wave heights

Schrodinger equation and motion in one dimension

The time dependent Schrodinger equation is

$i\hbar {\frac {\partial }{\partial t}}|\psi \rangle ={\mathcal {H}}|\psi \rangle$

where the state $|\psi \rangle$ evolves in time according to the Hamiltonian operator ${\mathcal {H}}$.

Motion in 1D

Operators, eigenfunctions, symmetry, and time evolution

Commutation relations and simulatneous eigenvalues Heisenberg and interaction picture: Equations of motion for operators Feynman path integrals

Discrete eigenvalues and bound states. Harmonic oscillator and WKB approximation

Harmonic oscillator spectrum and eigenstates Coherent states Feynman path integral evaluation of the propagator Motion in magnetic field WKB

Angular momentum

Commutation relations, angular momentum as generator of rotations in 3D, eigenvalue quantization Orbital angular momentum eigenfunctions

Central forces

Free particle in spherical coordinates Hydrogen atom

Continuous eigenvalues and collision theory

Differential cross-section and the Green's function formulation of scattering Central potential scattering and phase shifts Born approximation and examples of cross-section calculations Coulomb potential scattering Two particle scattering