Liquid Crystals 2

Introduction

As we know the common states of matter are: solid, liquid and gas; but there are many others states of matter, as plasma (just to say an example), that show different characteristics and behavior. Precisely we can think in a liquid crystal (LC) like a state of matter which is between solid and liquid and because that a LC can present characteristics of both states, but also can present new and interesting characteristics that have many applications in many brands of the technology that we use every day.

As we know a crystal is present when the matter has high order in the positions and also in the orientations of the particles. These isotropic properties are lost when the solid go to a liquid phase. Thinking in the liquid crystal, the molecules can flow as liquid and also may be oriented in a crystal-like way. Obviously, the symmetries present in a liquid are of higher order than a crystal. Therefore we can also think in a liquid crystal like a system which have intermediate symmetries between a crystal and a liquid. One of this intermediate symmetry could be respect with the orientation of the particles in the system.

Definition: A LC is a state of matter (most of the time form by organic compounds) which present properties between solid and liquid state of a crystal. Talking about symmetries is a system which present intermediate symmetries between a crystal and a liquid.

Overview of properties

Domains in a LC. Each color in this image represent a different domain in a LC and show how each domain have different optical behavior because each domain have different director.

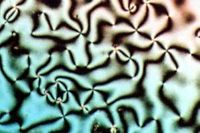
LC have the property that can flow as liquid, but also present domains with different orientation order. As we can appreciate in the right figure, each domain in this LC present different optical textures when is observed under polarized light. In each one of these regions the molecules are oriented in different directions.

Some crystalline solids can pass to liquid crystals due to a change in the temperature, these are call thermotropic liquid crystals. But the factors that determine the phase transition is not only temperature, also the concentration (generally in water) or actually pressure.

History

In 1888, Austrian botanical physiologist Friedrich Reinitzer , and his colleague von Zepharovich , working with some derivatives of cholesterol (cholesteric liquid crystals) found two different melting points in a derivative cholesteryl benzoate. With the help of the physicist Otto Lehmann found that the intermediate "fluid" was crystalline.

By that time, Reinitzer had discovered and described three important features of cholesteric liquid crystals: the existence of two melting points, the reflection of circularly polarized light, and the ability to rotate the polarization direction of light.

Lehmann continue with the studies of liquid crystals and in August of 1889 he had published his results in the Zeitschrift für Physikalische Chemie. The German chemist Daniel Vorländer continued the work of Lehmann and with the time he could synthesized most of the liquid crystals know.

In 1991, when liquid crystal displays were already well established, Pierre-Gilles de Gennes received the Nobel Prize in physics "for discovering that methods developed for studying order phenomena in simple systems can be generalized to more complex forms of matter, in particular to liquid crystals and polymers".

Phases (mesophases)

We can divide the types of LC by the phases that can be present. These phases can be divided in three:

-- Thermotropic phases

-- Lyotropic phases

---Metallotropic phases

Thermotropic phases

Consist of organic molecules where if the temperature is too high will be present a simple isotropic liquid phase (with obviously more symmetries). In the other side, if the temperature is too low then will be present a crystal solid (with less symmetries). Therefore these LC phases depend if we are in the right range of temperatures and actually could be present different type of thermotropic phases: smectic, nematic and cholesteric.

Smectic phase

The meaning of "smectic" has a Greek origin and means soap, because is it possible to find this phase precisely in the layer found in the bottom of the soap

This phase is present at lower temperature than the nematic phase. The molecules are present in well-defined layers that can slide over one another. In the Smectic A phase, the molecules are oriented along the layer normal, while in the Smectic C phase they are tilted away from the layer normal.

Nematic phase

This is one of the most common liquid crystals. In this phase the organic molecules (in a rod-like long shape) have no positional order, therefore the center of mass of each molecule has a uniform probability to be found in any place. In the other hand the particles have directional order. Therefore they can flow similar as a liquid, but present a preferential axis (could be more than one axis).

In this phase the molecules can be easily align by an external field and are use in liquid crystal displays. The preferred direction is given by a unitary vector n call the director and we can obviously see that this phase present a broken symmetry in the rotational isotropy.

To measure the degree or order in this phase is use the expectation value of the Legendre polynomial of second order:

$S=\langle P_{2}(cos\theta )\rangle =\langle {\frac {3cos^{2}\theta -1}{2}}\rangle$

Chiral phase (cholesteric phase)

The term chiral in general is used to describe an object that present asymmetry. Chirality (handedness) is refer in chemistry as a property of molecules having a non-super imposable mirror image. Therefore we can think in chirial molecules as molecules with no mirror plane. This phase in LC present chirality and it’s only for chiral molecules. A twisting of the molecules is present perpendicular to the director, with the molecules axis parallel to the director.

In the smectic C*phase (an asterisk denotes a chiral phase), the molecules have positional ordering in a layered structure (as in the other smectic phases), with the molecules tilted by a finite angle with respect to the layer normal. The chirality induces a finite azimuthal twist from one layer to the next, producing a spiral twisting of the molecular axis along the layer normal.

The chiral pitch, p, refers to the distance over which the LC molecules undergo a full 360° twist (but note that the structure of the chiral nematic phase repeats itself every half-pitch, since in this phase directors at 0° and ±180° are equivalent). The pitch, p, typically changes when the temperature is altered or when other molecules are added to the LC host.

Blue phases

These phases appear in the temperature range between a chirial nematic phase and an isotropic liquid phase. These phases present a regular cubic structure of defects of several nanometers, therefore show a Bragg reflections in the visible range giving the interest for many applications.

Discotic phases

In systems of plate-like molecules (instead of rod-like molecules) they can form discotic nematic phases, in which the molecules are align as shown in the last figure.

Lyotropic phases

This kind of systems consist of organic molecules that present liquid crystal properties under some range of concentrations rather than temperatures (as the system already discussed). In other words, for this type of LC it is necessary a solvent and another grade of freedom is added (the concentration).

In this phase the solvent molecules are filling the space around the organic molecules. In this type of liquid crystals not only the temperature is consider, also the concentration give a different type of phases.

Many amphiphilic molecules (with a hydrophobic part and also a hydrophilic part) present lyotropic phases. At low concentrations of amphiphilic molecules in a solvent (for example water), these molecules are randomly organized, but if we increase the concentration we will see that they will be assembling in micelles or vesicles (see figure) to hide the hydrophobic part and avoid to expose it to the water. At higher concentration this assembles will be order in some structure as hexagonal or cubic or also layers. These structure can also be arrange in different phases as nematic, smectic and columnar.

A generic progression of phases, going from low to high amphiphile concentration, is:

-- Discontinuous cubic phase (micellar cubic phase)

-- Hexagonal phase (hexagonal columnar phase) (middle phase)

-- Lamellar phase

-- Bicontinuous cubic phase

-- Reverse hexagonal columnar phase

-- Inverse cubic phase (Inverse micellar phase)

Metallotropic phases

Consist of organic and inorganic molecules.

Liquid crystal phases can also be based on low-melting inorganic phases like ZnCl2 that have a structure formed of linked tetrahedra and easily form glasses. The addition of long chain soap-like molecules leads to a series of new phases that show a variety of liquid crystalline behavior both as a function of the inorganic-organic composition ratio and of temperature. This class of materials has been named metallotropic.

Applications

LCD (Liquid Cristal display)

The properties of a liquid crystal in a electric field can be approach to organize its orientation and using some polarizers the control of the emission of light can be possible. Also using color filters it is possible to have pixels to generate red, green and blue.

In general the most common device is the twisted nematic cell. The distance between the top and bottom plates is of order of L=10micrometers. Appliying a voltage between the plates a normal electric field can rotate the molecules.

Qualitatively talking the pitch (4L) is much greater than the wavelength of the visible light and the direction of the polarization of light will follow the director, then using a polarizer just certain light is allow to pass to the cell. When the electric field is present most of the molecules will be perpendicular to the plane and won't change the direction of the polarization and the light is blocked. Therefore turning on and off the voltage the cell can be dark or clear.

Temperature measurement (by changing colours)

Thermotropic chirial LC whose dependence of temperature is strong can be use to “measure” the temperature. These devices are use in pools, baby baths, acquariums, etc.

Drug delivery

Using the vesicles form by hydrophilic molecules is possible to encapsulate drugs (or other compounds) increasing the specificity of the drug and enable slow release and also decreasing the toxicity. One problem of these methods is that by general result in an expensive way.

Theoretical treatment of liquid crystals

Firstable we need to define a way to describe the orientation of the molecules in the liquid crystal, to do this we talk about the director of the system.

Director: Is define as the preferred direction of the molecules in the LC.

Local Director: is the director in a finite volume of the LC.

The order parameter to measure the orientational tendency for the LC is define using the expected value of the Legendre polynomial of second order as:

$S=\langle P_{2}(cos\theta )\rangle =\langle {\frac {3cos^{2}\theta -1}{2}}\rangle$

where /theta is define as the angle between the molecular axis and the local director. For a isotropic LC the value is S=0 and for a perfectly align sample S=1. Therefore a typical crystal take values about 0.3-0.8 and, as is expected, at high temperatures will tend to zero because the thermal energy of the molecules.

Generally the order parameter is measure with one of these techniques: diamagnetism, birefringence, Raman scattering, NMR and EPR.

The positional order parameter is given by the variation of the density of the center of mass of the liquid crystal molecules along a given vector. In the case of positional variation along the z-axis the density ρ(z) is often given by:

Onsager hard-rod model

This is a model propose by Lars Onsager, which predict the lyotropic phase transition. This theory considers the volume excluded from the center-of-mass of one idealized cylinder as it approaches another. If the cylinders are parallel to each other, there is very little volume that is excluded from the center-of-mass of the approaching cylinder. If the cylinders are at some angle to one another, then there is a large volume surrounding the cylinder which the approaching cylinder's center-of-mass cannot enter.

While parallel rods decrease the orientational entropy, there is an increase in positional entropy. Thus in some case greater positional order will be entropically favorable. This theory thus predicts that a solution of rod-shaped objects will undergo a phase transition, at sufficient concentration, into a nematic phase. But because this model take many assumptions is hard to use it for real systems.

Maier-Saupe mean field theory

This model was proposed by Alfred Saupe and Wilhelm Maier. The potential that they use includes an attractive intermolecular potential from an induced dipole moment between adjacent liquid crystal molecules. This theory predicts thermotropic nematic-isotropic phase transitions, consistent with experiment.

McMillan's model

Proposed by William McMillan is an extension of the Maier-Saupe mean field theory used to describe the phase transition of a liquid crystal from a nematic to a smectic A phase. Predicts a triple critical point where the nematic, isotropic, and smectic A phase meet, but doesn't predicts its value. The model utilizes two order parameters that describe the orientational and positional order of the liquid crystal.

Elastic continuum theory

In this theory a liquid crystal is treated as a continuum and considers perturbations to a presumed oriented sample. There are three types of distortions: (1) twists of the material, where neighboring molecules are forced to be angled with respect to one another, rather than aligned; (2) splay of the material, where bending occurs perpendicular to the director; and (3) bend of the material, where the distortion is parallel to the director and molecular axis.