Phy5645/Double pinhole experiment
Submitted by team 1
Question: Double Pinhole Experiment
Besides the Stern-Gerlach experiment, the double slit experiment also demonstrates the difference between quantum mechanics and classical mechanics. Here, we will discuss a double pinhole experiment rather than a double slit experiment because the former is mathematically simpler and still embodies the basic physics that we wish to demonstrate.
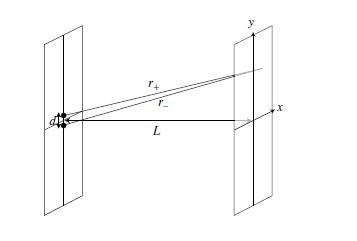
Suppose that a beam of electrons, traveling along the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z} axis, hits a screen at Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z = 0} with two pinholes at Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x = 0, y = \pm d/2} . For a point Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (x,y)} on a second screen at Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z = L>>d, \lambda} , the distance from each pinhole is given by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r_{\pm}=\sqrt{x^{2}+(y\mp d/2)^{2}+L^{2}}} . A spherical wave is emitted from each pinhole; the waves from each add, and the wave function at a given point on the second screen is
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi(x,y)=\frac{e^{ikr_{+}}}{r_{+}}+\frac{e^{ikr_{-}}}{r_{-}},}
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k = 2\pi /\lambda .}
(a) Considering just the exponential factors, show that the constructive interference appears approximately at
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{y}{r}=n\frac{\lambda}{d}}
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r=\sqrt{x^{2}+y^{2}+L^{2}}.}
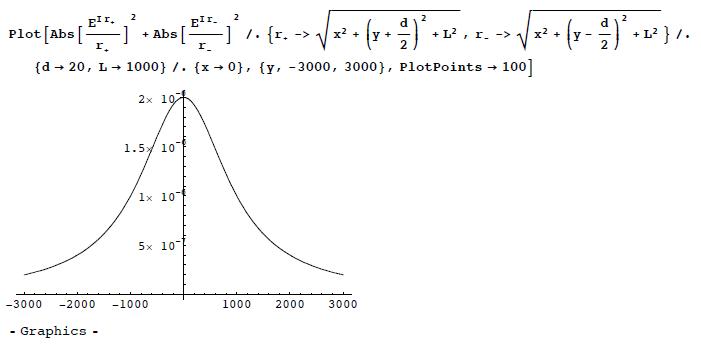
(b) Make a plot of the intensity Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\psi(0,y)|^{2}} as a function of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y} , by choosing Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k=1, d =20} , and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L=1000. } The intensity Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\psi(0,y)|^{2}} is interpreted as the probability distribution for the electron to be detected on the screen, after repeating the same experiment many many times.
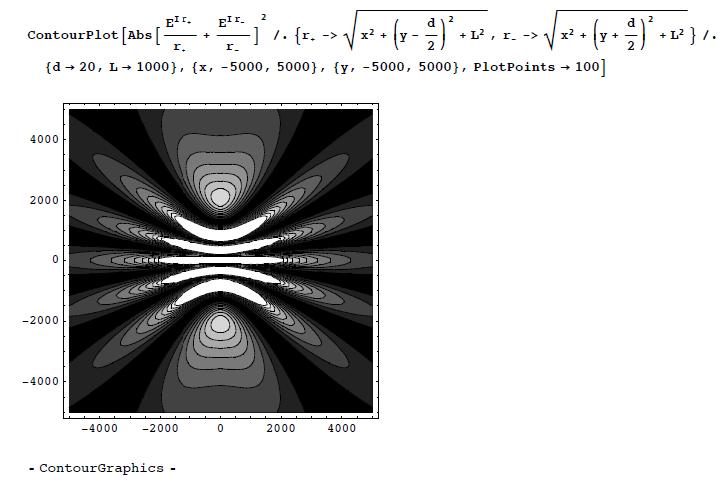
(c) Make a contour plot of the intensity Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\psi(x,y)|^{2}} as a function of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y} , for the same parameters.
(d) If you place a counter at both pinholes to see if the electron has passed one of them, all of a sudden the wave function "collapses". If the electron is observed to pass through the pinhole at Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y=+d/2\!} , the wave function becomes
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi_{+}(x,y)=\frac{e^{ikr_{+}}}{r_{+}}.}
If it is observed to pass through that at Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y=-d/2\!} , the wave function becomes
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi_{-}(x,y)=\frac{e^{ikr_{-}}}{r_{-}}.}
After repeating this experiment many times with 50:50 probability for each the pinholes, the probability on the screen will be given by
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\psi_{+}(x,y)|^{2}+|\psi_{-}(x,y)|^{2}\!}
instead. Plot this function on y-axis, and also show the contour plot, to compare its pattern to the case when you do not place a counter. What is the difference from the case without the counter?
Answer:
(a) As directed, we assume that the denominators are approximately the same between two waves. This is justified because the corrections are only of the order of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle d/l\!} , and we are interested in the case where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle d<<L\!} . We require that the numerators have the same phase, namely Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle kr_{+}-kr_{-}=2\pi n\!} . We expand the LHS with respect to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle d\!} ,
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} k(r_{+}-r_{-})&\approx k\left\{\left(\sqrt{L^{2}+x^{2}+y^{2}}+\frac{yd}{2\sqrt{L^{2}+x^{2}+y^{2}}}\right) \right. \\ &-\left.\left(\sqrt{L^{2}+x^{2}+y^{2}}-\frac{yd}{2\sqrt{L^{2}+x^{2}+y^{2}}}\right)\right\}\\ &=k\frac{dy}{\sqrt{L^{2}+x^{2}+y^{2}}} \end{align} }
Therefore,Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k\frac{dy}{\sqrt{L^{2}+x^{2}+y^{2}}}=2\pi n\!}
and hence
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{y}{\sqrt{L^{2}+x^{2}+y^{2}}}=n\frac{\lambda}{d}\!}
(b) Let us choose the unit where k = 1. Then we pick d = 20, L = 1000. Here is the interference pattern. First along the y-axis (x = 0):
(c) Now on the plane:
(d) For the same parameter as in (b), First along the y-axis (x = 0):
Now on the plane:
The main difference is the absence of the interference pattern.